The very first problem you will see test day will be a Quantitative Comparison one (QC). Indeed, the first seven problems will be QC, unless you decide to skip them (which in the case of the last couple may, for some, be a wise strategy).

Therefore, while prepping, you should make sure not to neglect QC, as it makes up over a 1/3 of the questions (remember, each question is worth the same points). To assess your ability on QC tackle the seven questions below. I’ve tried to make them similar in difficulty to what you’ll see test day.

The first question is the easiest, and the last the most difficult. That is, theoretically, the higher the number the more difficult the problem. I say theoretically because sometimes a question #6 turns out to be more difficult then question #7. Though, a question #3 will never be more difficult than a question #7.

What this means in terms of pacing is that you should not spend too much time at the beginning of the QC section. Yet, many do just that, thinking that they want to make sure to get the first few questions correct. So instead of checking your work several times on the first QC question, try to go through these questions quickly–but accurately–so you can spend more time focusing on the medium level questions.

That said, if you are struggling on the last couple QC (the difficult ones), then you should skip to other parts of the section and spend your time answering easier and medium level questions. With the questions below, you only have seven QC–as I didn’t want to write an entire GRE math section! So do you best, and see how many you can answer correctly in 12 minutes.

Note: all quantitative comparison questions have the same four answer choices.  I didn’t copy the answer choices for each question in this pacing drill, so please note the answer choices below:

a. Quantity A is greater.

b. Quantity B is greater.

c. The two quantities are equal.

d. The relationship cannot be determined from the information given.

1. The average price of a home County X is 250,000. The average price of a home in County Y is 300,000. The average price of a home in both County X and Y is 265,000.

A
The number homes in County X

B
The number homes in County Y

2.

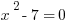
A
X

B
3

3. x + 1 = |x – 1|

A
x

B
0

4. Event X and event Y are independent. The probability of event X is 40%. The probability of events X and Y both occurring is 16%.

A
The probability of X occurring

B
The probability of Y occurring

5. A
The number of factors of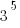

B
The number of factors of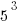

6. The area of a square is doubled.

A
The percent increase in one side of the resulting square

B
50%

7.

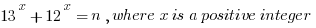
A
The number of distinct numbers that can be the units digit of n

B
4

Answers:
1. A

2. B

3. C

4. C

5. A

6. B

7. B