The Revised GRE is a long, grueling test. To get a perfect score on the quantitative section (a 170) you will not only have to answer the difficult questions correctly, but you will also have to answer all of the easy ones. Nonetheless, I’ve focused on the difficult questions for the 170-challenge. I can’t promise a perfect correlation, but something tells me that if you can answer all five of these questions correctly in less than 10 minutes, you are well on your way to a perfect score.
Of course missing a few hardly precludes a perfect score. But make sure you learn from the ones you miss to make sure you don’t make similar mistakes in the future. And if time is a problem, remember the Magoosh GRE product has plently of questions to help you hone your chops—both from a pacing and a conceptual standpoint.
Good luck, and feel free to post your answers. Let’s see who the first perfect score will be!
1. 
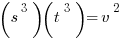If s and t are both primes, how many positive divisors of v are greater than 1, if v is an integer?
(A) two
(B) three
(C) five
(D) six
(E) eight
2. A quadrilateral has a perimeter of 16. Which of the following alone would provide sufficient information to determine the area of the quadrilateral. Choose ALL that apply.
[A] The quadrilateral contains equal sides
[B] The quadrilateral is formed by combining two isosceles right triangles
[C] Two pairs of congruent angles are in a 2:1 ratio
[D] The width is 4o% of the length and all angles are of equal measure
[E] If the perimeter was decreased by 50%, the area would decrease by 25%
3. Product Question: Triangle in a Parabola
http://gre.magoosh.com/questions/2192
4. If x is an integer, and 169 <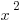 
< 324, which of the following is the sum of all values of x?
(A) 61
(B) 62
(C) 75
(D) 93
(E) None of the above.
5. x = 350,000
y = 45,000
| Column A | Column B |
|---|---|
| The total number of positive divisors of x | The total number of positive divisors of y |
- The quantity in Column A is greater
- The quantity in Column B is greater
- The two quantities are equal
- The relationship cannot be determined from the information given
[Note from our intern, Dylan: "I can do multivariable calculus, and got 2/5 on these in 10 minutes. These guys are tricky. 
"]
Explanation Video #1
Explanation Video #2
Explanation Video #3
http://gre.magoosh.com/questions/2192
Which is the best GRE Prep material out there that provides practice questions with the level of difficulty of these 5 questions?
Hi Lena,
I’d say there are only a few out there, besides Magoosh.
Manhattan GRE
Nova’s
GMATprep (Official Guide and GMATprep test)
Hope that helps!
rhombus is also one type of quadrilateral , then why should u neglect option A in second question
Let’s say you have a square with sides 4. Thus you have an area of 16. Now let’s say you have a rhombus with sides 4 but with two angles equal to 150 degrees each and the other two angles equal to 30 degrees each. Notice how this “squashed figure” would have a much smaller area than 14. Thus, (A) is not sufficient to answer the question.
Hope that helps!
did you mean to write by 75%*
Hi Chris,
I’m a little confused in your explanation about 3 answer choice e.
It says decrease the area by 25%, but you appear to be decreasing the area by 75%. Did you mean to write to 75% in the question?
Thanks!
(P.S. I’m watching this without sound so forgive me if i missed something vital)
Great catch! Thanks for noticing that
. It should be decreased by 75%.
I did not get any. I do not understand them. Do not know how to solve them. An explanation for all would be very helpful.
Thanks.
Julia
No problem, I will provide a video explanation. Coming very soon
.
Plz put up the explanations for all the questions. I got Q1 & Q2 wrong!
Okay, I will put up explanations for all of the questions
.
Are you going to post the video explanations?
Thanks.
Julia
Hi Julia,
Next week I will post the video explanation for #2, as that is the question everybody seems to be missing.
1) B
2) B, D
3) 0.25
4) E
5) C
It took me more time than it should have.
Anshul,
You answered most of them correctly
, except #2, which most people are missing. Take a look at answer choice (B) again.
On #4 I was able to get an answer of E,
because 14, 15, 16, 17 when added together =62
and then I used negative integers
-14,-15,-16,-17=-62
then I added the two sums and came up with 0 which wasn’t listed, so I chose E….I know my answer is right, but is my logic correct in how I got to that answer?
Yep your logic is correct, but there is an even faster way:
If you know that each solution for x has a positive and a negative answer (14, -14, 15…etc, then each will cancel out so you don’t have to worry about adding up all the positive integers than subtracting the sum of the negative ones).
Hope that helps
.
got my mistake
No problem
Shouldnt the answer to the second question be B and D? since b gives us all the angles and a square is formed and a quadrilateral can only be formed if we join them with a common hypotenuse ( equal in length).
1)B (s,t=2 and v=8)
2) B,C,D (I am not sure about option C)
3) 0.25 ( solve for 0.5 * k * 2*sq(k) = 1/8)
4)D (because k includes negative values as well, adding up to zero)
5) 60000 divisors each
for 350,000 divisors = 5 * 6 * 2 ( 350,000 = 2^4 * 5^5 * 7)
for 45,000 divisors = 5 * 3 * 4 (45,000 = 2^3 * 3^2 * 5^4)
I took 13 minutes but
Hi Praveen,
All of those are correct, except for #2, which seems to be stumping everyone
.
My clue for that question is try to think of two different shapes that can result from each condition. Just because you can think of one condition doesn’t mean that is the only condition. (Hint: a square + rhombus; rhombus + parallelogram).
Hope that helps
Let me retype Questions ## 4 and 5 as something went wrong in text after I posted
Question #4) answer E, 13^2<x^2<17^2
14,-14,15,-15,16,-16
Sum=0
Question #5) 350,000=5*7*(2*5)^4=5^5 *2^4 *7, (5+1)(4+1)(1+1)=60
45,000=3^2 *5 *(2*5)^3=2^3 *3^2 *5^4, (3+1)(2+1)(4+1)=60
answer C
Hi Pemdas,
All your answer and explanations are correct – except for #2:
(A) Not an answer
If the quadrilateral is a rhombus, then it will have a different area than if it was a square.
(D) Answer
We have the exact dimensions of quadrilateral: width = .6x, length = x, (x)(.6x) = 16. Solving for ‘x’ gives us only one positive value.
right, the area of rhombus is always less than the area of square. In our case if the quadrilateral is a square we get max.area=(16/4)^2=16, and if we have rhombus the area will be always less than 16. How I could miss it
Maybe I’ll make this a monthly challenge, so you’ll have another chance to get 5/5. Still, 4/5 is very good
.
Question #5) was merged with Question #4)
Question #5) answer is C
the whole task took me 9 mins
Question #1) when two primes factorized and raised to the power of 3 is perfect square the only viable case which comes to my mind is s=t=2 and (st)^3=(2*2)^3=64 or 8^2. Hence v=8 and 8=2^3 or (3+1) factors with 1 and 3 factors greater than 1.
answer B.
Question #2) I mark answers A and D
Question #3) answer 0.25, this one I knew answer ans solved earlier as have premium Magoosh account
Question #4) answer E, 13^2<x^2 (5+1)(4+1)(1+1)=60
45,000=3^2 *5*(2*5)^3=2^3 *3^2 *5^4, factors number –> (3+1)(2+1)(4+1)=60
answer C
1. A)
2. C), E)
3. 0.707
4. B)
5. A)
Hi Vanan,
As the post mentioned, these are some tough questions
.
Give it another shot, and see if you can get them right.