Linear equations are classified as a type of algebra problem in the official Core Math Study Companion, but they behave like function questions in many ways. A linear equation is an equation that states the way that two algebraic variables will always behave in relation to each other, even when the values change.
In other words, linear equations show variables that are dependent on each other—when the value of one variable changes, the other variable’s value will also change. And the changes will be predictable. To give a very simple example, suppose the values of x and y are connected, so that whenever the value of x goes up by 1, the value of y also increases by 1. This is pretty predictable, right?
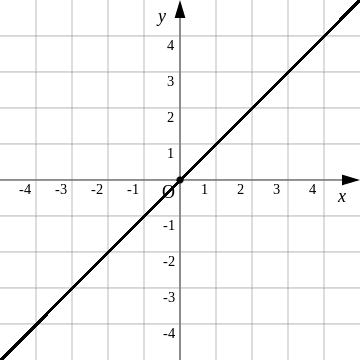
But even then, there still must be a point at which x and y intercept. This is the point at which x is 0. In the equation described in the above paragraph, if y is 0 when x is also 0, than the linear equation would be x = y. This is because x and y will always have the same value if they intersect at 0 and each number goes up by 1 when the other number increases by 1. You can see how the linear equation of x and y’s exact equivalency goes up in the following table:

table for linear equation x = y
This same relationship could be expressed by drawing a line (hence the name linear equation) on a coordinate plane:
graph for linear equation x = y
The linear equations you’ll come across in Praxis Core Math questions will be a good deal more complicated, of course. A more typical linear relationship might involve y increasing by 8 every time x increases by 2. 8 is four times as much as 2, so this means that y increases 4 times as quickly as x.
So in terms of the inter-related increase of x and y, y = 4x. Now if y and x both meet each other at 0, then y = 4x would be the correct linear equation. However, on the Praxis Core, the intercept will probably also be more complex than the example above. Let’s say that y is 3 when x is 0. To add this intercept to y = 4x, you can rewrite the linear equation as y = 4x + 3. On the Core Math test, the table for this equation would look like this:
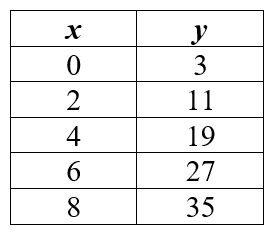
table for linear equation y = 4x + 3
And the graph for the equation might look something like this:
graph for linear equation x = y
Linear equation practice question, with table
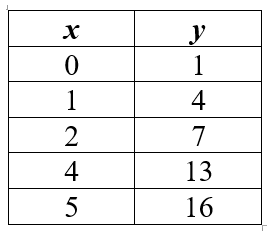
Which of the following equations expresses the relationship between x and y in the table above?
- A) y = x + 1
- B) y = 3x + 1
- C) y = x + 3
- D) y = 4x– 1
- E) y = 5x– 16
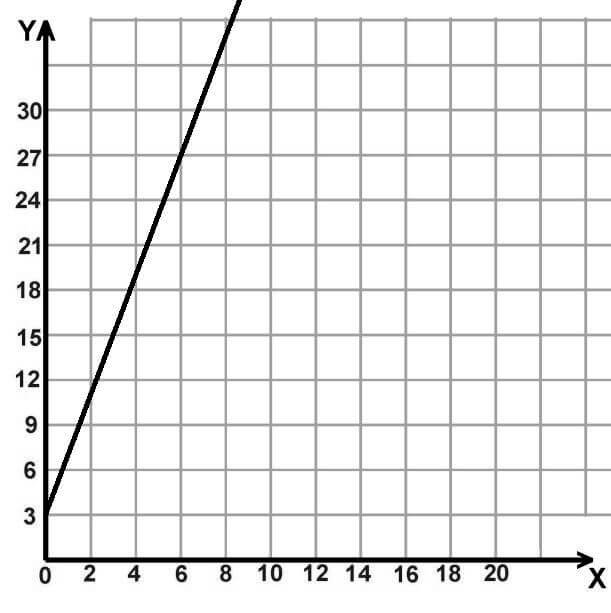
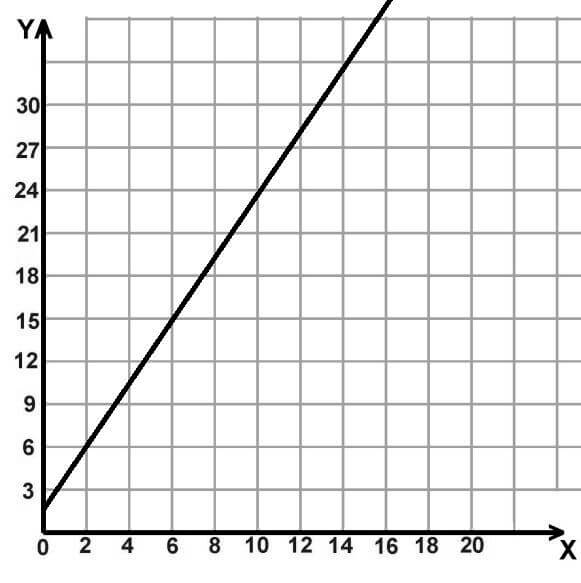
Linear practice question, with xy graph
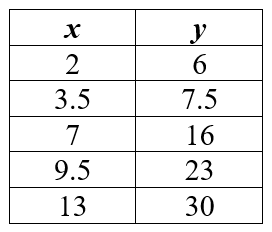
- The graph of a linear equation is shown in the xy -plane above. Which of the following tables of values corresponds to the graph?
- B)
- C)
- D)
- E)
Answer key
1) B
2) C
Answer explanations
For the table-based question, y has a value of 1 when it intercepts with 0 on the x axis. And you’ll notice that every time x increases by 1, y increases by 3. This gives us a linear equation of y = 3x + 1.
For the question based on the line graph of the xy plane, a lot of numbers aren’t clearly marked on the visual, since x is only marked in increments of 3, and y is only marked in increments of 2.
Fortunately, on Praxis Core Math problems like this one, you don’t need to worry about any number that isn’t explicitly labeled or might be a decimal. You only need to pay attention to the intercepts that are clearly marked whole numbers. On the chart, you can definitely see xy intercepts of (2,6) and (6,15). Answer (C) is the only choice that contains these two pairs of values.






Leave a Reply