If you’ve been studying GRE for some time, you’ve very likely encountered the following:
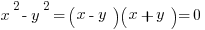 .
.
You may, however, only seen the following equation in the context of algebra. Nevertheless, the formula above applies to number properties. Let’s take a look.
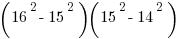
While you may be tempted to make a mad dash at it, calculating each of the squares, there is an easier way. Think of the ‘16’ as the ‘x’ and the ‘15’ as the ‘y’. Using the equation above we get:
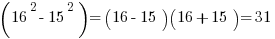 .
.
Wow, that was much easier than figuring out the squares of both ‘16’ and ’15.’ Now, let’s try it for the second pair:
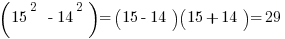
That leaves us with (29)(31). I know, you may be balking at my nifty little formula, thinking you still need to do some tedious multiplication. But despair not! We can still use the difference of squares formula:
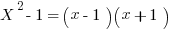
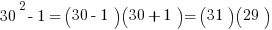
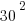 is simply 3 x 3 add two zeroes: 900. Then we subtract the one and we get 899.
is simply 3 x 3 add two zeroes: 900. Then we subtract the one and we get 899.
Next our two practice questions. The first question is not very different from the one above. The second one is more challenging and involves exponents.
Practice Questions
1. 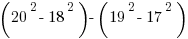 ?
?
- 4
- 36
- 38
- 76
- 224
2. 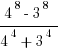 =
=
- 7
- 25
- 156
- 175
- 216
Explanations:
1. 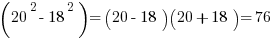
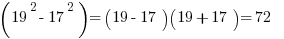
76 – 72 = 4, Answer (A).
2. 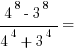
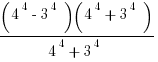
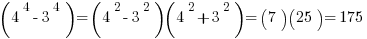 .
.






Leave a Reply