
Who wants a perfect 800 score in SAT Math? Who wouldn’t want that? Well, good news—that perfect 800 is within your reach. With the right prep, and the right understanding of SAT Math, anyone can get an 800, or something very close to it. We’ll share quick facts about SAT Math, steps you can take to get an 800, and share practice resources, including a free eBook filled with practice questions!
Aside from the obvious appeal of seeing that beautiful 800 glowing on your score report, there are other benefits to scoring perfectly in SAT Math. Whether you feel more confident in SAT Math or the Reading/Writing & Language sections of the test, a perfect Math score can keep your whole-test score high, making you a highly competitive applicant.
Table of Contents
- SAT Math: Quick Facts
- What Does it Take to Get an 800 in SAT Math?
- What are Some Steps I can Take to Get an 800 in SAT Math?
- Step 1: Master content first, then pacing
- Step 2: Keep an error log
- Step 3: Try to solve problems in multiple ways
- Step 4: Master every one of your weak areas
- Step 5: Master even the rarest of SAT Math content
- Step 6: Repeat, repeat, repeat!
- Step 7: Understand, don’t just memorize
- Step 8: Train yourself for minimal calculator use
- Step 9: Know and practice common strategies for SAT Math
- Step 10: Complete as many high quality practice questions as you can
- Where Else Can I Get SAT Math Practice?
- Frequently Asked Questions
- Get the Free Downloadable eBook!
SAT Math: Quick Facts
The first step toward SAT Math preparation is understanding. And by this, I mean you need to understand the basic structure of the test. It’s an easy first step. Consult the quick facts list and the two tables below, and you’ll clearly see the whole picture.
Fact #1: There are two sections of SAT Math: Calculator, and No Calculator.
The third and fourth sections of the whole SAT exam focus on math. Section 3 of the test is the first math section, and is headed “Math Test—No Calculator.” As you’d assume, you can’t use a calculator in this section of the test. Section 4 of the exam, the second SAT Math section, is entitled “Math Section—Calculator.” And—you guessed it—you can use a calculator in this part of SAT Math.
For full details on the differences between these two sections, check out the handy dandy table below:
| Test Section | Multiple Choice Questions |
“Grid-In” Questions |
Time Limit |
|---|---|---|---|
| No Calculator (20 questions) |
15 | 5 | 25 minutes (average 1 min., 15 sec. / question) |
| Calculator (38 questions) |
30 | 8 | 55 minutes (average 1 min., 27 sec. / question) |
| Whole SAT Math Section (58 questions) |
45 | 13 | 80 minutes |
Fact #2: Questions are either multiple choice or grid-in.
The majority of SAT Math questions are multiple choice. However, there is a smaller group of “grid-in” questions at the end of both SAT Math sections. Grid-in questions require test-takers to come up with the exact numerical answer themselves, and then enter the answer by filling in bubbles for the digits in the number.
Fact #3: Each question is worth the same amount of points.
Although there are two sections of SAT Math, the questions in these sections are equally weighted. A question missed in either section will have the exact same impact on your score. Moreover, you don’t earn more points for one topic or another. Whether a question deals with stats, trig, compound interest, etc., it will be worth the same amount as any other question. (And of course, multiple choice and grid-in questions are worth the same amount of points as well.)
Fact #4: Both sections focus on the same categories of math problems.
The College Board puts SAT Math problems into four categories: Heart of Algebra, Problem Solving and Data Analysis, Passport to Advanced Math, and Additional Topics in Math. Questions from these subcategories are distributed equally across the Calculator and No Calculator sections of SAT Math.
You can see the categories and their subcategories below:
| Category | Math Topics Covered | Number of questions per category |
|---|---|---|
| Heart of Algebra | -Linear equations and functions -Inequalities |
19 |
| Problem Solving and Data Analysis | -Ratios -Proportions -Percentages -Units of measurement -Quantitative data |
17 |
| Passport to Advanced Math | -Equivalent algebraic expressions -Quadratic equations -Exponents -Other nonlinear equations and functions (including expressions for lines on the coordinate plane) |
16 |
| Additional Topics in Math | -Geometry (2 dimensional and 3 dimensional) -Trigonometry (very basic trig) |
6 |
Fact #5: SAT Math is scored on a 200-800 scale.
Once all of your right and wrong answers have been tallied up, the College Board will convert your performance into a score between 200 and 800. This 200-800 range scaled score is what you’ll see on your official score report.
As you may have already realized, this 200-800 point range means that the two SAT Math sections (Calculator and No-Calculator) make up half of the 400-1600 range of your overall score for the exam. The other half of your SAT score is based on the first two sections of the SAT: SAT Reading, and the SAT Writing and Language Test.
What Does it Take to Get an 800 in SAT Math?
Now that you know the basic structure of the test, let’s look at exactly what it takes, score-wise, to get that flawless 800.
In some ways, it’s hard to answer this question concretely. You see, the SAT scores every test slightly differently. Your final scaled score (200-800 range) is based on your raw score (the number of questions you answer correctly). But each individual SAT exam has its own raw-to-scaled score conversion table. If you get a slightly harder-than-average mix of SAT Math questions on test day, the score conversion table is more “forgiving;” you’ll lose fewer points off your score for each missed question. However, if you get a mix of SAT Math questions that is of average difficulty or is slightly easier than average, missing even a single question can affect your score.
Now, no one can predict exactly what your raw-to-scaled score conversion will be for the SAT exam you personally take. But we can make a pretty educated guess at the possibilities. This is because the College Board has posted eight full practice SATs online, all of which contain questions from real past SAT exams. And each test comes with its own score conversion chart!
Below, take a look at the College Board’s sample of raw-to-scaled SAT Math score conversion. In the table, I’ve included the scores you need to get at least 750 on every test. This should give you some idea of what it takes to get a perfect or near-perfect SAT Math score.
SAT Math Score Conversion Table
| Raw Score | Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | Test 6 | Test 7 | Test 8 |
|---|---|---|---|---|---|---|---|---|
| 58 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 |
| 57 | 790 | 790 | 790 | 800 | 790 | 790 | 790 | 800 |
| 56 | 780 | 780 | 780 | 790 | 770 | 780 | 770 | 800 |
| 55 | 760 | 770 | 770 | 790 | 760 | 770 | 760 | 790 |
| 54 | 750 | 760 | 750 | 780 | 750 | 760 | 740 | 790 |
| 53 | 740 | 750 | 740 | 770 | 730 | 740 | 730 | 780 |
| 52 | 730 | 740 | 730 | 760 | 720 | 730 | 720 | 770 |
| 51 | 710 | 730 | 720 | 750 | 710 | 720 | 700 | 750 |
| 50 | 700 | 720 | 710 | 750 | 710 | 710 | 690 | 740 |
As you can see, more often than not, you need to get every single SAT Math question right in order to get that perfect 800. Even the two outlier tests in the table above require near-perfection. For Test 4, you can miss one question and still get an 800. And for Test 8, you can miss two questions (out of 58 questions) and still be “perfect” on your score report.
So what does this mean? Well, for one thing, it means you should train to get every single math question right on the test. The odds are very good that even missing one will knock your score down to 790. But the outlier tests also teach a valuable lesson: on test day, if you feel like you may have missed a question or two, don’t despair. You still have a chance at that perfect 800, perhaps a 25% chance, based on the available data.
Still, the best way to maximize your chances is to walk in on test day and answer every last question correctly. Does that goal sound daunting? In some ways, it is. But there are a number of steps you can take to make sure your chances at an 800 are really, really good.
What are Some Steps I can Take to Get an 800 in SAT Math?
If you’re aiming for 800, you need a solid action plan. Planning your studies can feel overwhelming, I know. But fear not! I’m about to walk you through a 10 step plan to get you all the way to 800, regardless of where your score is right now.
As you read these steps, please understand that the steps below are not necessarily one-after-the-other. The activities in these steps can and should overlap. You can decide which courses of action to start right away, and which to start a little bit later. But for the majority of your studies, all the activities below should be blended, done together in a winning combination. Roll up your sleeves, and we’ll get started.
Step 1: Master content first, then pacing
Nearly every SAT Math student I’ve ever tutored has the same complaint when they start studying. I always hear students complain that they are missing so many questions just because they run out of time.
As you start your path to full mastery of SAT Math, you need to think of problem solving and pacing as two separate skills. And you need to understand the relationship these two skills have to each other.
- Problem solving is the skill of doing math operations correctly.
- Pacing is the skill of doing math operations efficiently.
In other words, pacing isn’t just speed. If you do all of your math operations quickly but frequently get wrong answers, you aren’t being efficient, no matter how fast you are. Problem solving skills are the foundation for pacing skills. You need to learn how to do math operations the correct way before you can learn how to do them the efficient way.
So as you start really diving into SAT Math, don’t hold yourself to time limits at first. Instead, focus just on problem solving processes, and not on pacing at all. Them, slowly introduce timed practice and pacing. This can be done in phases, as follows:
Step 1, Phase 1
When you first start your practice, don’t use a timer at all. Just focus on doing the best you can on each SAT Math question you complete. At the end of each study session, see how many questions you’ve gotten wrong. Make a second attempt at any questions you missed, and then consult answer explanations to see if your second try was on the right track.
Step 1, Phase 2
Reach a point where you are consistently getting 75% accuracy or higher without having to go back and re-do any missed problems. Once you’re confident that you can maintain that level of accuracy, introduce a timer, but not time limits. Check the timer only at the beginning and end of each session, recording the timing of each practice session as a whole. Compare your total time to the total number of questions you answered, and look at your average time per question. You can still go back to re-work missed questions, but at this point you should be doing that after your timed practice session is finished. (In other words, re-done problems should not be factored into your accuracy or your pacing.)
Step 1, Phase 3
Continue practicing with a timer but no time limit. Now, however, you should start looking at your timer during practice. Begin to mark how much time you spend on each individual question. Flag and list any questions where you are considerably over the real SAT’s maximum average time per question (1:15 for the No Calculator section, 1:27 for the Calculator section). Then make note of the types of questions you are slowest with. Do some targeted practice with your slower question types, and work to get your overall average time per question down.
Step 1, Phase 4
Once your average time per question is at or near 1:15 per No Calculator question and 1:27 for questions where you can use a calculator, start holding yourself to the actual SAT Math time limits. You may find that your accuracy suffers a little when you first start to do this. This is normal, and your accuracy will come back. Keep working within those limits!
Step 1, Phase 5
Once you can get 75% accuracy or higher within the time limits, start trying to get 75%+ accuracy in less than the allotted amount of time. Try to maintain your accuracy while still having at least 5 minutes to spare in No Calculator, and 10 minutes to spare in Calculator. Use that extra time to go back and correct your questions for even greater accuracy. (And now that you’re comfortably in the time limit, going back to re-work questions does count as part of your accuracy and pacing!)
Step 1, Phase 6
Once you have good accuracy and the ability to go back and re-do problems as needed, try to reach a point where you can get 95%-100% accuracy in some of your practice sessions. Once that starts to happen, you’re in 800 range in terms of both accuracy and pacing. Keep up that good work!
Step 2: Keep an error log
An error log is a record of all the SAT Math problems that you get wrong. This kind of log, if done in the right way, can be a very powerful tool for getting an 800 in SAT Math.
Error logs for SAT Math should include the following information:
- Which problem you missed (chapter/page/problem number for problems in a book or PDF, URL/screenshot/problem name or number for online questions)
- What the correct answer was
- What your wrong answer was
- A brief description of what went wrong (for example: converted the fraction to the wrong kind of decimal, took the wrong approach, got confused and guessed, accidentally raised a number to the wrong power, etc…)
- Strategies and approaches that would have gotten you the right answer
Here is an example of what a typical SAT error log entry might look like:
Link: https://collegereadiness.collegeboard.org/pdf/sat-practice-test-3.pdf
Other info: Page 34 of test, question 7 of the No Calculator section
Skills Involved
f(x) function operations, plugging in values, subtraction with both negative and positive answers
Correct Answer
Choice C, gotten by recognizing that f(x) value is the result when an x value is plugged into an equation.
My Answer
B, gotten because I accidentally mistook the numbers in the f(x) column for the x values, and mistook the number in the x column for the end result of the equations.
Next Time I Should…
Be more aware of how f(x) tables work, and know that the function stands for the answer to the equation, and not for a value inside the equation.
As you maintain this kind of error log, you’ll notice certain patterns in your mistakes. You’ll see which types of math problems you most often get wrong. You’ll also see a pattern of winning strategies emerge—things you could have done differently for better accuracy.
When you have enough error log entries, you should summarize your error log information in two shorter documents. One of these documents should be a “cheat sheet” that lists all the most important strategies you’ve realized you need to follow. The other should be a “goal sheet,” where you list all the SAT Math content and problem types that you need to improve in.
Step 3: Try to solve problems in multiple ways
While you should definitely do longer SAT Math question practice sets, sometimes it’s also good to focus intensely on just one question. There is always more than one way to solve an SAT Math problem. Solving a problem in multiple ways can help you get a better sense of the very best way to solve a problem quickly and smoothly.
Let me show you a very basic example of this. Suppose you see this question on the SAT:
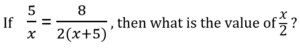
A) 50
B) 25
C) –0.08
D) –12.5
This problem has a lot of nuance, and there are a number of ways you could approach it. So it’s a good idea to experiment with them all.
Approach #1
Now, basically, what you need to do is solve for x and then plug x into x/2. The first thing you should do is simplify 5/x = 8/[2(x+5)]. But how? Well, you could multiply both sides by x. But if you take that approach, you’ll quickly realize things get messy, with result of 5 = {8/[2(x+5)]}*x. Could you proceed from there and still get the answer? Yes, but this approach is unwieldy, and doesn’t represent true simplification.
Lesson learned! That initial approach doesn’t work well. So let’s forget about multiplying both sides by x. In fact, let’s forget entirely about multiplying both sides by any one denominator. This is a dead end no matter which denominator you choose. Multiplying by a single denominator only shifts numbers form one denominator to another. That can create the illusion of simplification. But you want to actually simplify the equation.
Approach #2
To truly simplify things in a problem like this, the first thing you should do is look at individual fractions, not the equation as a while. So let’s look at the original equation again, fraction-by-fraction:
The 5/x portion is something you can ignore initially. There’s no way to simplify 5x. But that’s not the case with 8/[2(x+5)]. Here, the 8 and the 2 can be simplified. Let’s isolate those to get the fraction 8/2. This is the same as 4/1, or 4. So the 2 in the denominator can be eliminated, since it becomes a 1, and 1*(x+5) is the same as just 2(x+5). So now for the full equation, we have:
Approach #3
This is noticeably simpler, isn’t it? The next step in the simplification is to get rid of the denominators. And by this, I mean really get rid of the denominators, plural. Don’t just multiple one denominator by the other—make both denominators disappear at once. You can do this by using the “secret weapon” that will clear the denominators in any algebra problem like this one: cross-multiplication.
Cross multiplication works as follows: when a/b = c/d, ad = bc. In our simplified equation of 5/x = 4/(x+5), we have the following values for a, b, c, and d:
a = 5
b = x
c = 4
d = x + 5
This gives us a fraction-free equation of:
Approach #5
We can simplify that even further to get our answer:
x + 25 = 0
x = –25
Approach #6
From there, simply divide that x value by 2 to get your answer. But even in this relatively easy step, there are two different approaches you could take.
You could initially divide –25 by 2 in fraction form to get –25/2, and then convert –25/2 to –12 and 1/2, and then to –12.5. Or you could try to jump straight to the decimal, instantly seeing that –25/2 –12.5. Which approach is better? Well, going straight to the decimal is obviously faster. But if you “think” better in fractions, going from –25/2 to a mixed numeral and then to a decimal may actually be your best path to a correct answer.
Mind you, I’m not saying you should experiment with alternate approaches to every single practice problem; that would be very time consuming. But finding different approaches for a few problems a day can help you get a much stronger sense of the best way to approach any SAT Math question. And you’ll be able to avoid obvious missteps such as multiplying by one denominator, as seen above.
Step 4: Master every one of your weak areas
Error logging and finding different ways to solve problems will both help you identify your weak areas. Once you’ve found those trouble areas, you need to work on them aggressively. Don’t rest until you’ve truly mastered even your hardest SAT Math topics and problem types.
One way to really overcome your trouble spots is targeted practice. Is probability especially hard for you? Or perhaps geometry as a whole is difficult? Do practice sessions that consist entirely of problems from just one trouble spot. Focus on each spot, solving problems, error logging, learning how to improve, and ultimately improving.
There are a number of ways you can “cherry pick” problems from your weak areas. Search this very blog for practice math problems in your SAT Math trouble spots. You can do that by going to this custom Google search of the Magoosh High School Blog and adding in keywords related to your SAT Math weaknesses. And with a Magoosh SAT subscription, you can also use the Custom Practice settings in Magoosh SAT to select certain types of math problems.
And of course, there’s the good old fashioned method of going through an SAT Math practice book (or PDF), and manually choosing the best possible mix of practice questions in your weak areas.
Step 5: Master even the rarest of SAT Math content
I’ve already told you to leave no stone unturned when it comes to the content you’ve been getting wrong during practice. But you should also leave no stone unturned, period.
This means studying and mastering even the concepts that are very rare on the SAT, the ones that may or may not appear on test day. And be sure to study those rarer concepts thoroughly. If you miss a single concept in study and that concept turns up on the exam, getting just one problem wrong there (or anywhere) could lead to a 790 or lower.
So what does the study of these rare question types look like? To give one example, take trigonometry. Trig is a very rare SAT Math topic; you may only see one or two problems on the test. It might look like this problem (from Magoosh SAT):
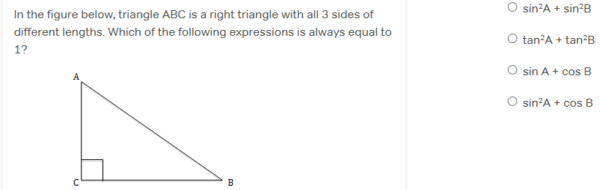
Here, you need to know the formulas for sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent). And then you need to look at those formulas and see which answer choice combination of them would always come out to a ratio of 1.
But what if the one trig problem you encounter in SAT is a different one, such as this one (also from Magoosh):
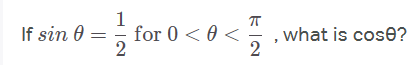
For this problem, you have to know the broader concept of SOHCATOA, the way in which every trigonometric triangle property relates to the other. (See Magoosh’s free video lessons for SOHCATOA Part 1 and SOHCATOA Part 2.) You also need to understand circle arc length as it relates to trigonometry (see the circle arc length tutorial for SAT Math).
As you can see, you never know quite what you’ll get when it comes to even a single rare concept. So you’ll want to study every single aspect of trig and do as many practice trig SAT Math problems as you can. The same goes for every math concept on the SAT. Whether a concept is relatively rare or extremely common, if you want an 800 in SAT Math, you must treat all concepts as equal. Even the rarest types of SAT Math are worth your full attention.
Step 6: Repeat, repeat, repeat!
What do practice questions, answer explanations, and tutorials have in common? All of them are worth reviewing for a second, third, or even fourth time.
In fact, if you don’t understand an SAT Math answer explanation or lesson, look at it again immediately. Feel free to stop and double check what you just read, watched or heard.
Never be willing to simply not understand something. And never assume you understand an SAT Math principle fully, just because you’ve explored it one time through. You’ll be surprised at how much more understanding you can gain when you go through material multiple times. This kind of hard work and willingness to retrace your steps will make you “math-wiser” and increase your chances of getting that perfect 800.
Step 7: Do NOT just memorize formulas, processes and patterns. Also truly understand them.
Formulas, processes, and patterns, oh my! These are the building blocks of solving SAT Math problems accurately and efficiently. For that reason, I’ve included a complete list of them in the eBook that comes with this article.
But you want to truly use these formulas, not abuse them. What is formula abuse, you may ask? Formula abuse is a common malady among SAT preppers; it’s the act of memorizing formulas without truly understanding them.
Without a decent understanding of why a formula works, it’s very easy to misremember a formula, or miss a step in a formula when applying it. In contrast, proper formula use involves picking a formula apart, really thinking about it and understanding why it works.
Understanding Formulas
Let’s look at an example of proper formula use. We’ll use (not abuse) the formula for exponential growth:
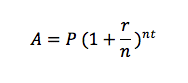
This formula is also sometimes called the compound interest formula, because it’s most often used to calculate the accrual of compound interest. In this equation P = principal (starting value), and r = rate of growth (interest rate). n = the number of time periods per year that the interest accrues. So for example, if the interest accrues monthly, we’d have a value of 12 for n, but if it occurs quarterly, n would be 4, for the four fiscal quarters of the year. Finally, t = time in years, and A = new amount after all interest has accrued.
But again, it’s not enough to merely memorize this formula and the meaning of each variable. And indeed, it’ll be hard to understand and recall the meanings of the variables if you don’t use them and test out the formula.
To test out this formula (and thus gain a deeper understanding of it), let’s plug in a few different values for P, r, n, t and A.
First, let’s say that we start out with $1,000 (P = 1,000), and then that initial amount earns 5% interest (r = 0.05), compounded quarterly (n = 4), for 11 years (t = 11). After 11 years, what’s our final amount (A = ?)?
Well, let’s run the numbers:
![]()
Crunching all of those numbers, you get approximately 1,000 * 1.73 for the interest. And yes, the numbers I’ve given you would likely be in the Calculator section, and the answer would be an approximation. So if the original $1,000 earned 5% interest, compounded quarterly, for 11 years, you’d have $1,730.
Now, here’s where you can really test a formula—we’re going to run a different set of numbers and see what the result is. In this case, I’d like to test and demonstrate the effect of a different compounding schedule. So I’ll keep the initial amount (P = 1,000) and the initial interest (r = 0.05) the same. We’ll also keep the total time period at 11 years (t = 11). But now, I’m going to say the interest compounded monthly (n = 12) and see what difference that makes:
![]()
So here, we have approximately 1,000 * 1.004^132 = 1,000 * 1.69. So the final amount is now $1,690 (A = 1,690). That’s a difference of approximately $40 if interest is compounded 4 times a year instead of once a year.
And you can explore this formula even further in many different ways. For example, what if the interest compounded annually (n = 1). Or what if the total time of interest accrual was cut in half (t = 5.5)? This kind of experimentation can help you understand what each variable in a formula truly means and does.
Understanding Processes: Question 1
This same kind of experimentation should be done with other processes and patterns found in specific SAT Math problems that you practice. Remember the example math problem I showed you in Step 3? To refresh your memory, it was the problem that looked like this:
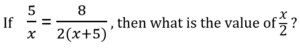
I actually based that problem on question 5 from the Calculator section of SAT Math on official SAT Practice Test 3. The original problem had different values in the equation, as follows:
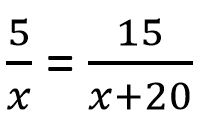
…And the original problem asked for different final value for the answer, specifically this one:
![]()
My changes to the numbers altered the outcome of the problem in different ways. For one thing, it made the final answer negative rather than positive. For comparison, see the answer to the original question in the College Board’s answer PDF for official SAT Practice Test Part 3.
Understanding Processes: Question 2
I did a few other experiments with the processes in this question as well. For instance, at one point I changed it to:
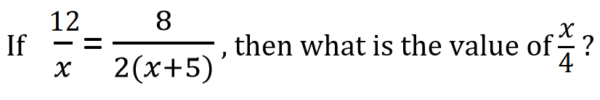
This got some really interesting results. Here, I didn’t just change the answer, but also some of the process. I wound up dealing with some fairly complex fractions-within-fractions toward the end. My final steps looked like this:
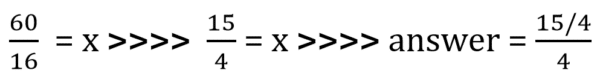
I ultimately got an answer of 15/16, or 0.9375.
Taking both formulas and actual practice problems and changing the values in different ways is a very powerful study tool.
Exercises like the ones above are especially useful if you want to get an 800, for two big reasons. First of all, it helps you to understand how the initial variables in a question determine the steps and outcome. In that way, you can see the steps and the answer coming. You can anticipate the possibility of tricky fractions, or changes to exponents, and so on. And you get a better sense for whether the answer you come up with actually feels right… or might be wrong. This kind of strong “number sense” is the exact trait you need to become an 800 SAT Math student.
Step 8: Train Yourself for Minimal Calculator Use
What if I told you that your calculator is a trap, a trick to fool you into getting the wrong answers? That on SAT Math, the Calculator section is still better done largely without a calculator? It’s surprising but true—you don’t need a calculator for most of what you do in the Calculator section. Not only that, but calculator use can open you up to mistakes you otherwise might not make.
Don’t get me wrong, a calculator should be used on the SAT when you both can use one and absolutely need to. However, there are two potential downsides to calculator use that you need to be aware of. Let’s go through those right now.
Calculator downside 1: Taking unnecessary extra steps
Mental math keeps your mind sharp, ever-searching for shortcuts and ways to simplify the problem. When you use a calculator, on the other hand, you tend to focus on completing processes rather than simplifying processes. You’re much more likely to key every single step of a problem into your calculator. And this sometimes makes a calculator solution take longer than a mental math solution.
Let me give you an example of a Calculator problem that’s both simpler—and yes, faster—to solve by mental math.
A) 105
B) 122
C) 130
D) 199
Here, if you used a calculator, you’d have to start checking the math for each answer, multiplying every choice by 1.3 (the multiplier for a 30% increase). 105*1.3 = 136.5, 122*1.3 = 158.6, and 130*1.3 = 169. So you’d be able to stop at the third choice and select it.
But let’s see how much easier it is without a calculator, relying on mental math techniques. In that case, you would probably start with a shortcut for calculating 30%. You’d realize that 30% is 1/10 times 3. So to figure out what 30% of any answer choice is, you’d need to divide the answer choice by 10 and then multiply that 1/10 of the answer by 3.
From there, a quick glance at the answer choices reveals something interesting. Because (C) is the only answer that ends in 0, (C) is the only answer where 10% is a whole number. So it’s the only answer where 30%, or a 30% increase, would also be a whole number. Since a 30% increase leads to the whole number 169, you’ve just eliminated answers (A), (B), and (D) effortlessly. If you have a keen understanding of mental math shortcuts, you can get to the answer almost instantly without a single calculator keystroke.
Here, the calculator could have wasted 15-20 seconds or so of your time. Think about how much that wasted time will add up if you needlessly use the calculator on 10, 20, or even 30 of your SAT Math Calculator problems.
Calculator downside 2: Keying in mistakes
It’s pretty difficult to write down the wrong number on a piece of scrap paper completely by accident. I mean, how often have you intended to write down, say, a 9, and accidentally written a 6 or 5 instead, without even noticing that you did that? I can’t imagine that’s happened very often to anyone.
If you look at your calculator keypad, you’ll know why I’m bringing this up. The 5 is diagonal from the 9 on most calculators, and the 6 is right below the 9. So these kinds of mistakes are easy to make on a calculator, yet wholly avoidable with mental math and pencil/paper.
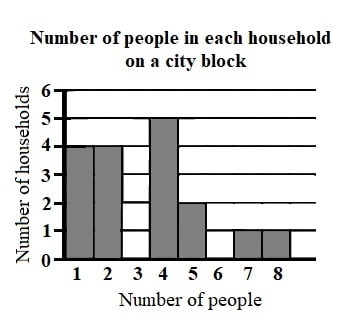
However, there’s also a less obvious way that calculators facilitate careless mistakes. To see how else the SAT Math Calculator section can lure you into keypad mistakes, let’s take a look at this problem:
A) 3
B) 4
C) 5
D) 6
Because there are so many numbers, it’s tempting to try to use a calculator to keep track of them all. You need to divide the total number of people on the block by the number of households. Now, there are 17 households total; this is easy enough to add up with or without a calculator. But what about the total number of people? To get that with a calculator, you’d enter this operation:
Unfortunately, when you use a calculator to deal with info from a graph, you’re not focusing much on the full meaning of the graph. Instead, your energies are devoted to transferring numbers from the visual to the calculator. So you could easily transfer numbers that you shouldn’t.
For example, you might accidentally include a 3 and a 6 in the figure for total people among the households. In our haste to copy numbers from the chart to the calculator, you may not think about the fact that there are zero households with those numbers of people. In that case, your calculation would incorrectly look like this:
With that mistake, you get 66/17 instead of 57/17. 66/17 leads you to a number that rounds up to 4 (an incorrect answer), while 57/17 would round down to the correct answer of 3.
It would actually be far safer to use scrap paper or mental math for just about every step in this problem. The only point at which a calculator might be useful is the very end, when you actually divide the number of people by the number of households. Otherwise, the calculator really is a trap that can cause you to miss an otherwise manageable question.
How to train yourself to use the calculator less
Basically, you need to treat every Calculator problem as a challenge. The challenge is to do the entire problem, or as many steps as possible, without a calculator.
Be creative! Think of shortcuts you can take to skip steps, make other steps go faster, and get to that answer quickly, just through brain power. And speaking of shortcuts, that brings us to Step 9 on your path to an 800 in SAT Math…
Step 9: Know and practice common strategies for SAT Math
Strategies are the lifeblood of your SAT Math performance. On problems where it’s useful, be sure to try backsolving—starting with the answer choices, and then seeing which answer choice best works for the question. (You saw this in the first example problem in Step 8 above.) Be sure to use other common strategies as needed, too. Sometimes estimation will get you to the right answer choice quickly. Other times, replacing the variables with numbers you’ve picked will make it easier for you to understand an algebra operation in SAT Math.
In general, you want to cultivate a strong “number sense,” so that you can identify and use the right mental math tricks for various questions in SAT Math. For more instruction on this, with lots of tips and examples, check out the downloadable eBook!
Step 10: Complete as many high quality practice questions as you can
When it comes to getting an 800 in SAT Math, practice makes perfect. But not just any practice. There are plenty of low-quality SAT Math practice questions out there. Poorly designed SAT Math practice won’t match what’s actually on the exam, and can leave you unprepared for the real test. Be sure to seek out high quality resources from reputable companies.
This blog is a good place to start. Here, you’ll find excellent SAT Math practice in our free resources, such as the Guide to a Perfect 800 in SAT Math eBook.
Where Else Can I Get SAT Math Practice?
There are quite a few places to get good SAT Math practice. Check out the lists below.
Magoosh SAT Math Practice
In addition to the eBooks I mentioned in the previous section, you can also practice SAT Math with:
- Magoosh’s free SAT Practice Test PDF
- Magoosh’s Public SAT Video Lessons
- Magoosh SAT Premium (approximately 350 practice SAT Math questions, well over 100 SAT Math video lessons)
College Board SAT Practice
The College Board, the company that makes the real SAT exam, offers a generous amount of free practice in SAT Math, along with practice questions for the rest of the exam.
- Official SAT Practice Tests (free online resource, includes 8 full tests in PDF, with essay questions and answer explanations)
- SAT Sample Questions (additional free online test questions for SAT Math, SAT Reading, and SAT Writing and Language)
- The Official SAT Study Guide (The practice tests in this book are also available online, through the above-linked Official SAT Practice tests. However, this book also offers additional model practice questions and tutorials, as well as a chance to practice the SAT in paper form, like you would on test day.)
Khan Academy SAT Prep
Khan Academy has worked closely with the College Board to create additional official prep for SAT Math. (And for the other parts of the exam, of course!) Here is what they have to offer:
- SAT Math Practice (The practice problems come in video form, with a video lesson on how to solve each problem; there are 79 video lessons in all. This is a companion practice set to Khan Academy’s similar SAT Reading and Writing practice.)
- Full-length SAT (in addition to the full-length practice tests from Magoosh and College Board, Khan provides one of their own)
Other sources of SAT Math practice
I definitely recommend Magoosh, College Board, and Khan Academy as the very best sources of SAT Math practice. But needless to say, these three sources aren’t the only ones out there. Should you try any additional publishers and companies? You just might want to. Read Magoosh’s SAT book reviews and decide for yourself.
Getting an 800 in SAT Math: Frequently Asked Questions
If you want the very top score in SAT Math, there are a few important things you need to know. Here are some answers to ambitious SAT Math students’ frequently asked questions.
What is the math on the SAT?
This is a great question. As I’ve mentioned before, you really do need to know every possible math topic on the SAT if you want to get an 800.
The College Board puts SAT Math into four categories: Heart of Algebra, Problem Solving and Data Analysis, Passport to Advanced Math, and Additional Topics in Math. But obviously, these sometimes poetic-sounding category names don’t tell the whole story. Let’s take a closer look at what kind of math is actually in these categories.
Heart of Algebra deals with regular algebraic equations, and with functions, by which I mean the problems that use the notation f(x) to indicate a certain type of algebraic function. Heart of Algebra also deals with algebraic inequalities in addition to regular equations.
Problem Solving and Data Analysis is dominated by word problems and infographics. You’ll need to calculate proportions and rations of different things to each other. You’ll also deal a lot with percentage changes, units of measurement, and other types of quantitative data.
Passport to Advanced Math is the next step up from Heart of Algebra, in terms of difficulty. Here, you’ll solve systems of algebraic equations, and algebraic equations where there is more than one possible answer. This category of SAT Math also includes quadratics and other algebraic equations where one or more of the variables is a square or exponent. Expect to deal with many exponent-related problems, and many problems where x, y, or other variables have two possible values, or sometimes more.
So, what are Additional Topics in Math, exactly? While the College Board-given name implies this is a generic mix of extra math, there is in fact a common theme: geometry. Expect to deal with coordinate geometry, three-dimensional geometry (volume, surface measurements for physical objects, etc.) and two-dimensional geometry (area, angles, shape, and so on). Here, you’ll also see some trigonometry, advanced mathematics in 2D geometry, focusing on the properties of triangles and circles.
Is there any calculus on the SAT?
There are no calculus math problems on the SAT. However, within the “Passport to Advanced Math” category of questions, there are some math problems that could be thought of as “pre-calculus.”
The more advanced math problems on the SAT will include complex algebraic expressions and functions that might also be seen in some easier calculus problems. However, what you do with those functions on the SAT will be different from what you’d do with them in calculus. You won’t be using calculus methods to evaluate functions, and the answer choices won’t be the kinds of results you’d typically get in a calculus math problem.
What is the highest level of math on the SAT?
This question is a little tricky. In terms of the typical high school learning sequence for math, trigonometry is probably the most advanced content in SAT Math. However, not everyone learns math in the same sequence at their high school.
More importantly, not everyone finds the same kinds of math to be hard or easy. When students ask what the highest level of SAT Math is, they are usually really trying to figure out what the hardest SAT math is. And for that, your individual mileage may vary. Typically, SAT test takers find trig and the complex systems of algebraic equations to be the hardest.
However, I’ve also talked to plenty of students who are reasonably comfortable with trig and Passport to Advanced Math, but find something else to be really challenging. (This “something else” could be a certain type of word problem, a certain aspect of the exponential growth formula, specific kinds of shapes in geometry, and so on.) Anyone aspiring to a perfect 800 in SAT Math should work diligently to discover and address their own personal weaknesses.
Free Downloadable eBook: The “How to Get a Perfect 800 in SAT Math” PDF
Hopefully the information and steps in this article can guide you as you work toward your perfect score. But we’re not done yet! Magoosh has also made an eBook to help you along the way. This eBook lists the strategies you should practice and the formulas you should truly understand.
We’ve also given you 20 practice questions (with answer explanations) so you can actively use those strategies and formulas. These questions cover all of the math content you’ll see on the test.
Good luck, and here’s to a perfect 800!






Leave a Reply