SAT Math Practice: How to Study Smarter and Score Higher

Even though he gets himself into more dangerous situations than he maybe needs to, Harry Potter is actually an awesome role model for your SAT Math practice. In fact, the general Hogwarts system of education is pretty solid in the first place. They don’t just send students off to fight Death Eaters on their first day. Nope—it takes years and years of hard work for students to go from levitating feathers to producing patronuses (patroni?).

What’s that have to do with SAT Math practice? A whole lot.

The good news is that you won’t need seven years for your SAT Math practice. But you will need some dedicated practice over a period of time—and the willingness to push yourself. Nobody made Harry take on all of those challenges, you know. (Well, maybe Lord Voldemort.) But other than the Dark Lord, that kid was pretty darn self-motivated.

So what other lessons can we glean from Harry to help you with new SAT math practice? Well, quite a few. (Maybe that’s not so surprising. Those books get deep!) For example: How long did it take you to read all seven books, again? A couple months? That’s actually, in an ideal world, about how long you’d ideally prep for SAT math!

What else? Read on…

Don’t Underestimate Good SAT Math Practice

Sure, there are students who can sit down and ace SAT Math on their first try. But that’s a really, really rare scenario, involving a combination of luck and previously developed skills. Think about the troll Harry, Hermione, and Ron find in the girls’ bathroom in the first book. They basically get that thing by accident. Why by accident? Because they haven’t learned enough to knock the troll out on purpose yet!
 

Translation? If you want to actually know how to master SAT Math, you’re going to need to start SAT Math practice. Taking SAT practice tests is a good place to start. Remember that regular practice over a longer period of time is more useful than intense practice over a shorter period—you’re more likely to retain the information in your long-term memory.

Not sure how to make this work in your schedule? Here are some awesome SAT study schedules to help you out (as well as some SAT Reading practice and SAT Writing and Language practice to incorporate!).

Accept that SAT Math Is Its Own Thing

Don’t despair if your scores on your first new SAT practice test aren’t as high as you’d like them to be. This is a standardized test, and there is a set of standard material that it tests over…and over…and over. One reason students don’t see this at first is because the SAT likes to bundle simpler concepts together into mega-problems.

While a question may actually be testing relatively basic algebra and geometry principles that you’ve seen a million times, for example, the combination of those principles is what makes these problems into more of a challenge. (Think of Hogwarts classroom practice compared to a wizard’s duel.) That’s why you should…

Practice One Topic at a Time—At First

Actually, let’s make that learn and practice one topic at a time. While you’ve probably already seen SAT Math topics in your math classes, it may have been a while since you had to think about algebra (or even pre-algebra!). In fact, be ready to show off your knowledge of:

• Algebra
• Averages
• Combinations and permutations
• Data interpretation
• Exponents
• Functions
• Geometry
• Integer properties
• Probability
• Percentages
• Sequences
• Statistics
• Word Problems (which touches on many SAT Math topics)

But for most of us, “showing off” isn’t exactly what comes to mind when reviewing that list of topics. With that in mind, complete lessons—in a book, online, or in person—that emphasize in-depth practice of one mathematical area before moving onto another. This is particularly important in the early days of your SAT Math practice, when blanking on a process you learned three years ago can make you miss valuable points!

However, you should also be taking regular SAT practice tests around once a week, because seeing those questions mixed together in all of their glory (or, you know, test-day context) is pretty important. And that’s why, a few weeks before test day…

Get Ready for the Mental Game

Once you’ve reviewed all of the math areas that the SAT tests, kick your practice into high-gear with sets of SAT Math questions. When Harry Potter gets into trouble, he can’t just produce a patronus every time; he has to mix up his skills a little bit. And the same is true for SAT Math—you’ll need to be used to changing gears quickly by test day.

If moving from averages to functions, or exponents to permutations, throws you off, start your practice by creating sets of problems you’ve already done, whether in practice sets or on practice tests. These don’t have to be long; 10 problems will be enough to start with. Ease yourself into the hodge-podge that is SAT Math by working through these problem sets before practicing with new problems.

It can really help to keep a list of the subject areas tested by the problems you get wrong. You may find that it’s not geometry problems that give you trouble—it’s only geometry problems that involve exponents. Or it’s not number properties that you need to review—it’s number properties as they’re used in probabilities. The more precise you can be, the more targeted you can make your practice.

Think Mathematically

As you do more and more new SAT Math practice, you’ll find that the SAT rewards nimble thinking. By that, I mean leaping from one concept to another easily. The above practice strategies will help you do that, but you can also improve these skills in real life by thinking mathematically.

Need to calculate a tip? Leave your phone in your pocket. Splitting the bill? See if you can do it mentally before breaking out the calculator. As you start relying on your brain rather than your calculator, more and more, you’ll see that this will not only make you faster on test day, but it can also help you get through problems more efficiently. Sometimes it’s really not important that the product of two numbers is 44.75—sometimes, it’s enough to mentally estimate that the product is 45.

Developing your mathematical thinking will help you forego overuse of your calculator (yes, even when the test allows you to use it, after that first no-calculator math section!) and get through those problems quicker and with more confidence.

Speaking of confidence…

Focus on Your Strengths

Harry Potter knows he’s not good at Divination, all right? Granted, he doesn’t really seem to practice it that much, but he’s aware that Defense Against the Dark Arts is his strength. And even when he has a totally impractical teacher, he goes off and practices on his own.
 

Be like Harry! As you continue your SAT Math practice, don’t forget to check in regularly with your strong areas. After all, you don’t want to lose points that you normally would have gotten just because you’re rusty.

Similarly, on test day, skim through the Math section and circle problems it looks like you’d be good at (particularly if timing is an issue for you—but don’t take more than a minute to do this!). By getting through those problems first, you’ll not only feel better about the test in general, but you’ll also be able to get more points if time runs out before you get to all the questions.

Ready for the Sequel? Try These SAT Math Practice Questions

Whether you’re totally new to SAT Math or you want a little extra practice, here’s a bonus: SAT number properties questions! (I know, I know—is it your birthday already?!) Happy practicing!

SAT Math Practice Question 1

In the three-digit integer XYZ, in which X, Y, and Z each represent a different integer, 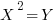. If XYZ is even, how many different integers can it represent?

A. 2
B. 5
C. 8
D. 10

(answer below)

SAT Math Practice Question 2

If 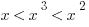, which of the following must be true?

I.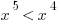

II.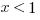

III.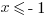

A. I only
B. II only
C. I and II only
D. II and III only

(answer below)

SAT Math Practice Question 3

The sum of 4 distinct integers is 29. If the greatest integer is less than 10, what is the least of the four?

A. 0
B. 3
C. 5
D. 6

(answer below)

SAT Math Practice Question 4

When the prime number k is multiplied by 2, the result is 1 less than another prime number. Which of the following is NOT a possible value of k?

A. 2
B. 3
C. 5
D. 7

(answer below)

SAT Math Practice Question 5

If a and b are distinct positive integers and 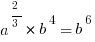, then what is one possible value of b?
 
(answer below)
 

Question 1 Answer

In the three-digit integer XYZ, in which X, Y, and Z each represent a different integer, 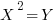. If XYZ is even, how many different integers can it represent?

Answer: (C)

Explanation: First, set up three spaces on your paper for that three digit integer.

__ __ __

We’re going to have to plug in a couple of numbers to these digits and look for a pattern. Never hesitate to plug in. Let’s start with 1.

1 __ __

But that would make Y=1 also, and the question told us that X and Y are different integers. No go.

So let’s try X=2.

2 __ __

That means Y=4.

2 4 __

So two-hundred and forty-something works. But because it’s even, we can only put five numbers into the last blank: 0, 2, 4, 6, or 8.

BUT keep in mind that the digits have to be distinct! That means neither 2 nor 4 can be Z, because they’ve been used for X and Y already.

So we have three possibilities. (A) is out. Can we pick other numbers for X? Try 3.

3 __ __

3 9 __

This time, we can use all five even digits numbers for Z. So we’re up to eight possibilities. (B) is out.

And let’s try another…

4 __ __

4 16 __

16 can’t be a digit. That means 4 is too big to be the value of X, which means our only options were 2 and 3. So we have a total of eight numbers to be XYZ.

Shortcut: Since we know that Y can’t be greater than 9, and Yis X squared, we know that X can’t be greater than 3. Then just check 2 and 1 quickly.

Question #2 Answer

If 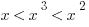, which of the following must be true?

I.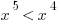

II.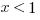

III.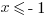

Answer: (C)

Explanation: Again, plug in some numbers! The question gives us some hints as to what to try in I, II, and III. Since I is a bit hard to test, start with II.

If 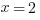, then 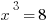and 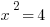, so that doesn’t work. And we can rule out any other positive integer for the same reason; increasing the exponent increases the value. And 1 is out, since it neither increases nor decreases with an exponent. So II is true. That eliminates (A).

Next, let’s check III.

If 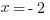, then 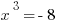and 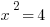. That means 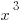is the lowest of the three, so that doesn’t make sense. And, come to think of it, all negative numbers will follow the same pattern, going from negative to positive to negative as the exponent increases. So we can eliminate III, which means that (D) is gone.

Now we know that X must be between -1 and 1. Plug in 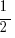and 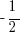to check III, and you’ll see that 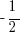works. So (C) it is.

Shortcut: Since 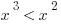, we know that 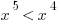must be true. Both have a larger, odd exponent creating a lesser value than a smaller, even exponent. There’s no real number that would work in one of those inequalities and not the other.

Also, knowing that natural numbers always increase with larger exponents would prove fact II right away. No number greater than 1 would follow the strange pattern provided. Then it’s just a matter of plugging in negative less than -1 to check III.

Question #3 Answer

The sum of 4 distinct positive integers is 29. If the greatest integer is less than 10, what is the least of the four?

Answer: (C)

Explanation: Use the numbers in the answer choices if you’re not sure how to tackle this. Since we’re looking for the least, we’ll start by checking (A).

If the lowest number is 0, then the other three together must total 29. But if they’re all less than 10, that’s not possible. The highest they can be is 9+8+7=24. So (A) is out.

(B) gives us a similar problem. The other three would have to total 26, but 24 is as high as we can get.

(C), on the other hand, works. 29 – 5 = 24, and we already know that’s possible.

Shortcut: In order to get a very low number in a set that adds up to something specific, we want to use the highest possible numbers for the others in the set.

For example, if we were trying to get a sum of 10 from two numbers, and we wanted to use a low number like 1, we’d need to pair it with a high number, 9.

In this case, we use the highest possible numbers—9, 8, and 7—for the other three, and then just check what the difference is. 29 – 24 = 5.

Question #4 Answer

When the prime number k is multiplied by 2, the result is 1 less than another prime number. Which of the following is NOT a possible value of k?

Answer: (D)

Explanation: Once again, we’re going to want to use these answer choices to our advantage. In fact, we have to. Any question that asks “which of the following is NOT” has to be solved by process of elimination.

So let’s take (A). If k is 2, then multiply that by 2 to get 4. Is 4 one less than a prime number? Yep. 5 is prime.

For (B), 3 multiplied by 2 gives us 6, which is one less then 7. Since 7 is prime, this also works. Cross it off.

(C) has the same problem; 2 times 5 is 10, which is one less than 11.

(D) is the only one that doesn’t make another prime. 2 times 7 is 14, which is one less than 15, and 15 isn’t prime.

Shortcut: Since you have to go by process of elimination, there isn’t a faster way to do this, really. Writing out 2k + 1 = prime might help you speed up your math, though.

Question #5 Answer

If a and b are distinct positive integers and 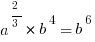, then what is one possible value of a?

Answer: 8, 27, 64, 125, or any other perfect cube.

Explanation: No answer choices to work with here… and it’s not immediately obvious if plugging in any old number for the value of a or b will help us.

We need to simplify the equation. Get b on only one side.

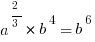
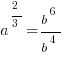
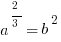
Then get rid of that root 3 by cubing each side.

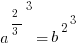
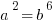
Get the square root of each side to make it simpler.

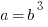
And you’re pretty much done. We know that b is an integer, so plug one in—say, 2—and the value of a is 8. Or whatever else, depending on what you choose for b.

Shortcut: Once we get to 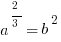, we can cancel out the 2s in each exponent to get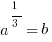

And since we know b is an integer, a must be a perfect cube; just pick one.