SAT Math: Heart of Algebra

Heart of Algebra is one of 3 sections on the SAT Math test, and will include 19 of the total 58 questions. In short, “Heart of Algebra” refers to any problem that has an algebraic equation in which none of the powers next to a variable is higher than one. For example:

Pretty straightforward, right? The computation underpinning Heart of Algebra is straightforward, but the SAT typically won’t be giving you problems this simple. While you will encounter several problems that ask you to solve for variables, much of the Heart of Algebra content are real-world word problems that you have to unwrap before solving. For example:

How to Prepare for the SAT Heart of Algebra section

There are two ways to make sure you’re prepared for Heart of Algebra questions:

1. Understand how to solve linear equations and systems of equations, along with common variations, like inequalities.
2. Practice translating real-world scenarios and information into a mathematical equation.

To help you get the swing of things, we’ve broken down and demonstrated the key concepts and skills that will serve you in the Heart of Algebra section. Feel free to explore these concepts through the clickable table of contents below:

Algebra Basics: Balancing the Equation

First thing’s first: in order to interpret real-world scenarios as equations, you’ll need to be super clear on how to balance an equation!

So, in an algebraic equation with an equal sign, think of the equation in balance. If you do anything to one side you do the exact same thing to the other side. If you multiply one side by 4, you have to multiply the other side by 4. If you subtract 3 from one side, you subtract 3 from the other side.

The goal in balancing the equation is isolation. That’s right — you want to isolate x, or get x (or whatever variable happens to be in the equation) by itself. Think of the variable as the unpopular person in the room. Everyone – that is, the other numbers – want to get away!

\(4x + 3 = 15.\)

To get x by itself, first subtract 3 from both sides of the equation.

\(4x + 3 – 3 = 15 – 3\)

\(4x = 12\)

Now divide both sides of the equation by 4:

\(frac {4x} {4} = frac {12} {4}\)

\(x = 3\)

Let’s try one more:

\(sqrt{x} = 9\)

Notice how x has a square root sign on top of it. We want x to be all by itself. Therefore we have to get rid of the square root sign by squaring both sides:

\((sqrt{x})^2 = 9^2 \)

\(x = 81\)

The gist? By knowing how to isolate variables by balancing equations, you’re well on your way to success on the Heart of Algebra section!

Inequalities

Although inequalities may seem tricky, if you’re comfortable balancing equations, you shouldn’t have much problem with balancing and solving inequalities. The main way that inequalities differ from equations is that the sign changes if you multiply or divide by a negative number.

Inequalities come up a lot on SAT Heart of Algebra, so if you need a refresher, make sure to check out this video:

System of Equations

Now, let’s apply a more advanced version of balancing equations to a very important concept in Heart of Algebra: System of Equations.

System of Equations refer to when you have two equations with two unknowns and by combining these two equations, you can solve for these unknowns. There are two methods for combining equations: substitution and elimination.

For a refresher on these methods, check out the below video and then try your hand at solving the practice problem that comes after:

Algebra Basics Practice: System of Equations

Now, let’s go back to that original question we started this post off with:

Coordinate Geometry Basics

Ok, let’s break down each of the concepts you’ll need to understand, step-by-step, to fully grasp coordinate geometry.

Quadrants

There are 4 quadrants in a coordinate plane.

Simple, right?

What’s wonky is how those quadrants are arranged on the plane:

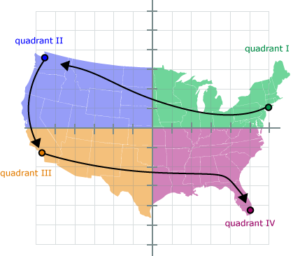
A good way to visualize the quadrant layout is to imagine yourself on a cross-country trip in which you start off in New York (the northeast = quadrant I), drive on over to Seattle (the northwest = quadrant II), then drive down to Los Angeles (southwest = quadrant III) and finally end up in Miami (southeast = quadrant IV).

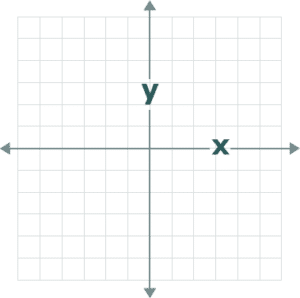
The X-Axis & Y-Axis

The next things to be familiar with are the x-axis and the y-axis. The x-axis runs from left to right (this is the horizontal line), whereas the y-axis runs up and down (this is the vertical line).

Integers and Scale of Graphs

Next, you need to understand integers, or what we like to call “people numbers.”

Why people numbers? Think of it this way: you can have one more person or one person fewer. However, you can’t have .3 people or ½ a person. In “coordinate geometry land,” you’ll have integers running from left to right, like on a number line, from negative to positive. On the left hand side the negative numbers will decrease until they hit the middle of the graph (the intersection of the x- and y-axes—or what’s known as the origin). At that point, you’ll see the number zero. Then the numbers continue up from zero.

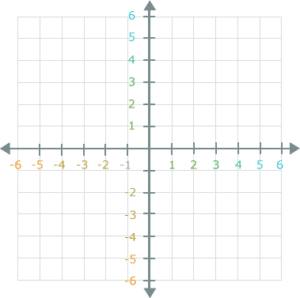
For the y-axis, the vertical one, the negative numbers start at the bottom, decreasing until they get to zero. Then, from the origin going up, each number will go up as well.

On the SAT, the scale of the x- and y-axes will vary from question to question. Not all axes increase and decrease on an interval of 1. Sometimes, the scale of the x-axis will be totally different from the scale of the y-axis! The test-makers will try to trick you on this point with the answer choices, so definitely make sure to pay attention to the scale of each axis.

Coordinates

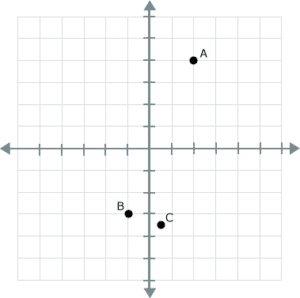
Next up are the coordinates. Coordinates are always presented as two numbers: the first number corresponding to the x-axis, and the second one to the y-axis. For instance, in the graph below, point A has the coordinates (2, 4). That is you “go over” two points to the right on the x-axis and up four points on the y-axis. Point B has the coordinates (-1, -3).

Even though the numbers on the x-axis and y-axis are always broken down via integers, coordinates can have fractions, as point C shows below (1/2, -7/2).

Slope

Ok here’s the fun part that involves putting together the basics from above.

Remember the term “Rise over Run”? You’ve probably had this hammered in for so long you can’t even remember when you first heard it. Sadly though, most people forget exactly what it means.

So here it is: you can figure out the slope of a line by seeing how many squares on the coordinate plane one point is above the other. In the graph below, point D has a y-coordinate of 2 and point E has a y-coordinate of -3. So point D is five squares higher than point E. This is the “rise,” how far up it goes from the lowest point, is 5.

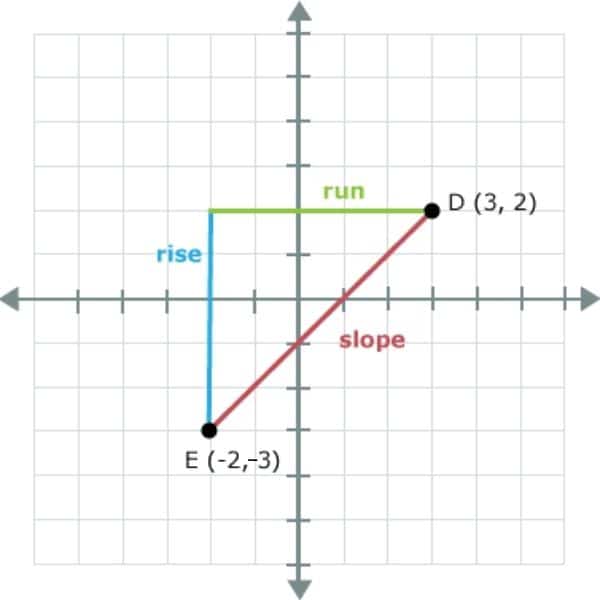
When you are figuring out the slope, which consists of a fraction, always put the “rise” in the numerator.

The “run,” on the other hand, is how far away two points are in a left-to-right sense.

If you count how many squares point D (3, 2) is from point E (-2, -3), in a left to right sense, you’ll get the “run,” which in this case is 5.

Maybe you’re wondering why on earth it’s called the “run.” It’s just one of those conventions you have to learn. The key is you always put the “run”, or whatever you want to call it, in the denominator.

Now, the good news. There’s actually a faster way of doing this besides just counting squares! It’s all in this formula (which your algebra teacher would hate me for leaving out):

For example, let’s have \(y_2 = 2\) (the y-coordinate in point D) and \(y_1 = -3\) (the y-coordinate in point E). That means \(x_2 = 3\) (the x-coordinate in point D) and \(x_1 = -2\) (the x-coordinate in point E). Using the formula, we’ll get:

\( 2 – (-3) \)
_______
\(3 – (-2)\)

which equals:

\( 5/5 \) or \( 1 \), meaning that the slope is 1.

If you switch the order, the equation will look like

\( -3 – 2\)
_______
\(-2 – 3\)

which equals:

\( -5/-5 \), which is also \( 1 \).

Coordinate Geometry Practice

Every now and then, the SAT gets diabolical and throws a coordinate geometry question without the coordinate plane. To make matters worse, the question is usually difficult to begin with—even if you had the plane.

The key is to translate the information by drawing out a mini-coordinate plane. Remember, this is a timed test, so it doesn’t have to be anything fancy (don’t worry, the test isn’t going to require you to carefully graph out parabolas the way your math teacher does). As long as your graph can help you better visualize the problem, you’re halfway to getting the problem right!

Of course, the other half is always a bit tricky. Case in point: the question below. If you’re able to crack it in less than two minutes, you’re in excellent shape for Heart of Algebra!

If you have a comment or question about this problem, leave it for us below!

Functions

You’re going to find about 2-6 function questions on your SAT, and if you haven’t been working with them recently in math class, they might throw you for a loop.

Just to be clear, we’re talking about equations that look a bit like this: \(g(x) = frac {x-4} 2\)

You may have a couple of immediate reactions to equations like this.

For one, you may have the instinct to graph it out right off the bat, which is great, but not necessarily what you’ll need to do on the SAT.

Or, if you’re not so familiar with functions, you might make a lethal error and assume the \(g\) here is a variable. It’s not, by any means, but it’s also important to note that these functions aren’t always a separate skill from solving algebraic equations. They’re just wearing costumes: \(g(x) = frac {x-4} 2\) is the same thing as \(y = frac {x-4} 2\).

Although function questions tend to come later on in the section, which is typically where the hardest questions on the test are found, functions are really not that difficult and can be solved pretty quickly with some practice. If it helps, you can change the function notation to look like an algebraic equation that you’re more familiar with.

Try that concept out with relatively simple function question, based on the equation above:

Here are some things to keep in mind about functions:

The “g” in g(x) Is Just Shorthand

Let’s say you have a friend who has a particular way of eating grapes. Let’s call her Gina. And let’s say Gina brings grapes to school every day, eats four, splits the rest into two equal piles, then throws away one of the piles and gives away what’s left.

The thing is that she brings a different number of grapes every day. Meaning, what she gives away at the end also varies. Does this sound familiar? You might recognize this process from above. It’s just an example of that earlier function \(g(x) = frac {x-4} 2\), where:

• x is how many grapes Gina comes to school with originally
• \(4\) represents how many grapes Gina eats
• \(frac {x-4} 2\) represents both the pile that Gina throws away AND the pile she gives away, and
• \(g(x)\) is just shorthand for Gina’s process: \(frac {x-4} 2\)

What that \(g\) really means is a process (not the final result) without writing out each step of the way. Gina brings \(x\) grapes, and she then “\(g\)s” the grapes. In a way, “\(g\)” a verb, not a noun.

Functions Inside of Functions

So let’s say you’ve got a whole group of friends with unique grape-eating habits. Gina does her grape ritual and then hands off what’s left to Hailey. Hailey goes through a whole other process. She won’t eat Gina’s grapes unless she gets the same amount of grapes from somebody else, and she then squashes one of them under her foot.

So Hailey’s equation would be \(h(x) = 2x – 1\). What she has, then, is described by \(h(x)\). But first we need to think about how many Gina gave away.Then, put the two processes together into one: \(h(g(x))\). Take it from the inside out, and you’ll have no problem.

If Hailey’s grapes are passed along to even more friends with specific grape eating habits, just keep nesting the function, e.g. \(f(h(g(x))\). On the SAT, you likely won’t go beyond one function nested in another.

In the end, SAT functions like this will end up being no different than the simpler-seeming SAT equations. Really.

Functions Practice: Nested Practice

Let’s try out Gina and Hailey’s equations with a practice question:

Heart of Algebra: You Got This!

The above concepts really do constitute the “heart” of the Heart of Algebra section, so if you familiarize yourself with them and practice these types of problems, you’ll be in great shape! For more practice problems, make sure to check out SAT Math: Algebra Practice Questions.

You can also check out the other question types on SAT Math, like Problem Solving and Data Analysis, read more about how to score a perfect 800 on the SAT math section, and check out some additional SAT Math practice!