Calculus is primarily the study of rates of change. However, there are numerous applications of derivatives beyond just finding rates and velocities.
In this review article, we will highlight the most important applications of derivatives for the AP Calculus AB/BC exams.
Applications of Derivatives
Here is a list of some of the essential derivative applications.
- (Instantaneous) Rates of Change
- Velocity
- Acceleration
- Slope and Tangent Lines
- Analysis of Graphs
- Increase/Decrease
- Relative Extreme Points
- Concavity
- Inflection Points
- Related Rates
- Optimization
Rates of Change
Perhaps the most important application of the derivative is in finding rates of change. In fact, this is why Newton (and Leibniz independently) invented Calculus in the first place!

Suppose y = f(x) is a function that models some real-world behavior. Here, the input is x and output is y. A natural question in the sciences is: How does the output change as one changes the input? In other words, what is the change in y resulting from a change in x?
For most purposes, it makes sense to consider the ratio of the changes. For example, if y changes twice as quickly as x, then that would be a rate of change of 2.
So this leads to the concept of average rate of change, Δy/Δx. (See AP Calculus Review: Average Rate of Change for more about this.)
Finally, by allowing the change in input to approach 0 (by taking a limit), we get the definition of derivative:
![]()
Of course after you learn the definition, then you get to learn all of the shortcut rules for derivatives that let you avoid taking limits at all!
Example: Rates of Change
Suppose the population of a small city can be modeled by P = 40532 e0.03t, where P is total population and t is time in years after the year 2000. How quickly was the population increasing in 2002?
Solution
The phrase “how quickly” means “at what rate”? So we use a derivative to find the rate of change.
P ‘ = 40532 e0.03t (0.03) = 1215.96 e0.03t
The year 2002 corresponds to t = 2.
P ‘(2) = 1215.96 e0.03(2) = 1291.15
Thus the city was growing at a rate of about 1291 people per year.
Velocity and Acceleration
By definition, velocity is the rate of change of position. So, if you have a position function s(t), then the velocity function is nothing more than the derivative of s(t).
Analogously, acceleration is the rate of change of velocity – hence the second derivative of position.
Slope and Tangent Lines
The derivative value f ‘(a) measures the slope of the curve y = f(x) at the point x = a. By extension, then the derivative also gives you the slope of the tangent line there.
Here is another reference for tangent lines and slopes of curves: How to Find the Slope of a Line Tangent to a Curve.
Example: Tangent Lines
Find the equation of the tangent line to the curve y = (1/3)x3 – (1/2)x2 + 3x – 5 at x = 6.
Solution
Slope = Derivative. Here, dy/dx = (1/3)3x2 – (1/2)2x + 3 = x2 – x + 3.
Therefore, the slope at x = 6 is:
m = (6)2 – (6) + 3 = 33.
We also need the y-coordinate of the point. So plug x = 6 into the original function as well.
(1/3)(6)3 – (1/2)(6)2 + 3(6) – 5 = 67.
Finally, using point-slope form, we construct the equation of the tangent line.
y – 67 = 33(x – 6) = 33x – 198, or
y = 33x – 131
Analysis of Graphs
There’s quite a lot that Calculus can tell us about the shape of a graph. We’ll focus on what the derivative and second derivative can say about a graph.
For a detailed review of these topics, you can also check out: AP Calculus Exam Review: Analysis of Graphs
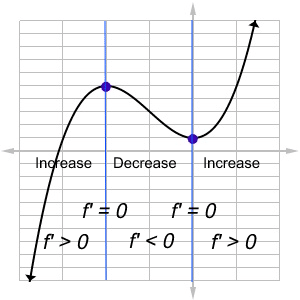
First Derivatives — Increase, Decrease, and Relative Extrema
The first derivative measures the slope of the curve. So just as slopes of lines can tell you whether the line increases, decreases, or is horizontal, the derivative can be used to locate intervals of increase and decrease, as well as any turnaround points.
| If f ' > 0 | f is increasing (on an interval) |
| If f ' < 0 | f is decreasing (on an interval) |
| If f '(a) = 0 | f has a critical point at x = a |
At a critical point, the graph may turn around (but it’s not a guarantee). Then you can use the First Derivative Test to decide whether each critical point is a relative maximum, minimum, or neither.
First Derivative Test: Suppose x = a is a critical point for a function f.
- If the sign of the derivative f ‘ changes from positive to negative at a, then there is a relative (local) maximum at x = a.
- If the sign of the derivative f ‘ changes from negative to positive at a, then there is a relative (local) minimum at x = a.
- Lastly, if the sign of the derivative f ‘ does not change at a, then there is no relative extreme point there.
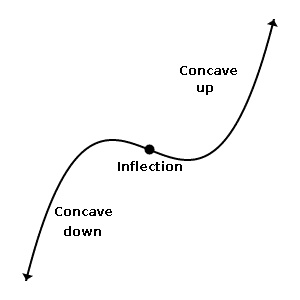
Second Derivatives — Concavity and Inflection Points
Second derivatives give you information about concavity (direction of curving), and inflection points (transitions between different concavities).
| If f '' > 0 | f is concave up (on an interval) |
| If f '' < 0 | f is concave down (on an interval) |
| If f ''(a) = 0 | (a, f(a)) is a possible point of inflection |
For more details, check out: AP Calculus Review: Inflection Points.
Related Rates
Sometimes the behaviors of two quantities are tied together. For example, raising the temperature of a gas in a fixed container will raise its pressure as well.
The method of Related Rates can be used to understand how rates of change are related based on an algebraic or geometric relation among the original variables.
Because the word “rate” appears in this topic, it should be no surprise that derivatives will be used!
Example: Related Rates
A spherical balloon is filled with helium at a constant rate of 5 cm3 per second. How quickly is the radius increasing when the radius is 16 cm?
Solution
First we need to remember the volume formula for the sphere. This relates the two variables mentioned in the problem: volume (V) and radius (r).

First, we take time derivatives of both sides of the volume formula to produce a related rate.
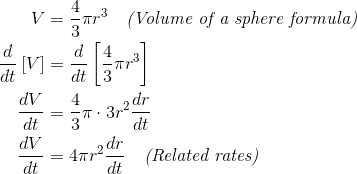
Next, we plug in the known information, dV/dt = 5, and r = 16.
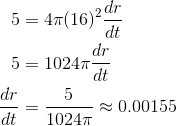
Thus, the radius is increasing at 0.00155 cm per second.
For more practice, try this link: AP Calculus Review: Related Rates.
Optimization
Optimization is simply the process of finding a maximum or minimum value. However, in most optimization problems, there is more than one input variable and certain constraints on the variables. So it takes quite a bit of algebra to set up the function before you can take its derivative.
Understanding optimization problems really takes seeing a fair number of them worked out. You can find a detailed review of optimization here: AP Calculus Review: Optimization.
Summary
Now that you’ve seen the various ways in which applications of derivatives can appear on the AP Calculus exams, you can be more confident on test day! Just keep in mind a few key concepts from which all of these applications arise.
- Derivatives measure rates of change.
- Derivative values are slopes.




Leave a Reply