This review article is all about optimization. Here, you’ll learn the tools and techniques for setting up and solving these often difficult problems. And along the way, we’ll work out a few examples!
Optimization
The method of optimization uses derivatives to find maximum or minimum values. However, the functions that need to be optimized typically have more than one variable. Hence, considerable work goes into transforming the problem into a single-variable function first.
Let’s introduce the methods using a concrete example.
Example: A Widget Factory
Suppose you own a business that makes and sells widgets. If you sell x widgets at a price of p dollars each, then that earns your company a total of xp dollars. By the way, the quantity R = xp is called the revenue.
So why not just charge a huge price for each widget to earn the most money you can? After all, the objective of most successful companies is to maximize their revenue.
Well, you would raise prices, except that you noticed in the past that every time you did so, there were fewer sales of widgets. In other words, as p increases, x decreases.
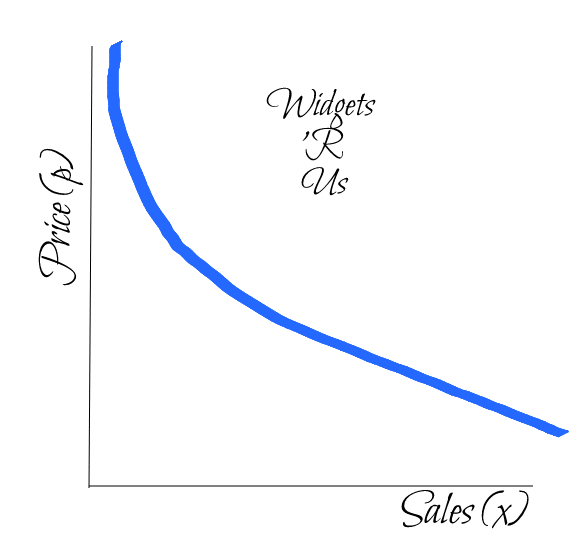
Fortunately, if you know exactly what the relationship between price and number of widgets sold at that price (or demand), then you can use optimization to find the price that maximizes your revenues!
Using the Relation to Reduce Variables
Next, suppose that we add one vital piece of information to this problem: The relationship between price and demand is given:
x = 400 – 40p + p2, for 0 ≤ p ≤ 20
Note, any equation that relates the variables of an optimization problem is a constraint equation.
Now do you remember that revenue function? (In case you forgot, it was R = xp.)
Let’s use the relationship between x and p replace x to create an objective function having only one variable.
R = xp = (400 – 40p + p2)p = 400p – 40p2 + p3
Using the Derivative to Find the Maximum
Now that we have a single-variable expression, we can use the usual techniques from Calculus to find its maximum value.
First take the derivative of the objective function:
R ' = 400 – 80p + 3p2
Next, set the derivative equal to zero to locate any critical points. Here, we’ll have to use the Quadratic Formula.
400 – 80p + 3p2 = 0
p = 6.67, or 20.
Because we got two answers, we have to check which one (if any) gives the correct result. Plugging in each one into the revenue function, we find:
R(6.67) = 400(6.67) – 40(6.67)2 + (6.67)3 = 1185.18
R(20) = 400(20) – 40(20)2 + (20)3 = 0
Clearly p = 6.67 gives better revenue.
(By the way, since there was a restriction that 0 ≤ p ≤ 20, we do not have to worry about what the revenue function does beyond p = 20.)
Solving the Original Problem
According to the work above, the price should be p = $6.67. Then, to find the actual number of widgets that produces this amount, simply plug into the constraint.
x = 400 – 40(6.67) + (6.67)2 = 177.7
Rounding to the nearest widget, your company should produce and sell 178 widgets at a price of $6.67 each to achieve a maximum revenue of (178)(6.67) = $1,187 (approximately).

Method of Optimization
So what have we learned from the above example? Even though most of the work was peculiar to this situation (revenue, price, demand, etc.), there are a number of steps that are useful in general.
- Read the Problem carefully. (This should go without saying.) Identify what you are trying to maximize or minimize (the objective) and what relationships exist among the variables (constraint equation).
- Write the objective as well as any constraints in terms of the variables in the problem.
- Use algebra to solve the constaint(s) and reduce the number of variables in the objective. The goal is to express your objective function in terms of only one variable.
- Use calculus to find the max or min of the objective function. This means taking a derivative, setting it equal to zero, solving, and determining which solutions give the appropriate answers for the given problem.
- Make sure you answer the original question. You might have to find the values of the other variables or quantities now.
The hardest thing about optimization problems is the setup (Steps 1-2), because that changes from problem to problem.
Example: Rectangles and Parabolas
Find the largest area possible for a rectangle inscribed between the parabola y = 9 – x2 and the x-axis, with its base on the x-axis.
Solution
First, let’s sketch the graph of the parabola as well as a typical inscribed rectangle.
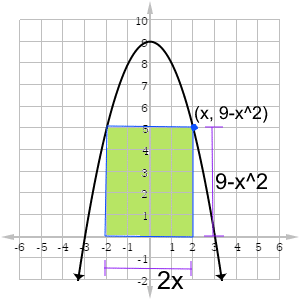
Our objective is to maximize the area of the rectangle.
Area of a rectangle: A = bh.
Because the parabola touches the rectangle at its upper corners, we know that the height of the rectangle is the same as the y-coordinate of the upper right corner point. That is, h = y = 9 – x2.
The base length of the rectangle is b = 2x (a distance of x on the left and the right side).
The two equations above are the constraints. Let’s replace the variables b and h in our objective function by their equivalent expressions in terms of x.
A = bh = (2x)(9 – x2) = 18x – 2x3
Now we can take a derivative and set it equal to zero.
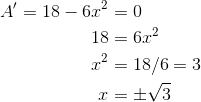
Of course, only the positive x-value makes sense in this context. Plug x = √3 into the area formula (objective function) to find the maximum area.
![]()





