Related Rates problems are any problems where we are relating the rates of two (or more) variables. They come up on many AP Calculus tests and are an extremely common use of calculus.
AP Calculus Review: Related Rates
There is a series of steps that generally point us in the direction of a solution to related rates problems. No two problems are exactly the same, but these steps are a very good rubric for solving a wide variety of problems:
1. We must first identify the variables which are changing in the problem. This could be size, volume, distance, etc.
2. Find the governing equation which relates the variables. This is often given in the problem, or is a relatively well-known relation (i.e., volume = length × width)
3. Rates are usually (for AP Calculus) in relation to time. Therefore, we differentiate both sides with respect to time.
4. Substitute in the known rates of change and/or known quantities
5. Solve for wanted rate of change or quantity
Common Errors:
We always plug in known values of variables after finding the derivative, never before finding the derivative.
A difficult Related Rates example.
(Note: this is a more difficult than normal problems in its set up. We have simpler sample problems following.)
A ladder with a length of 1 meter is leaned up against a building. It’s a bit off balance, and so beings to slide away from the building at a rate of r m/s. What is the rate that the top of the ladder moves while sliding down the building when the base of the ladder is b meters from the building?
1. Variables: what changes with time?
a. Speed of the top of the ladder
b. Distance of base from the building
2. Governing equation:
a. Drawing this problem makes it easy to visualize.
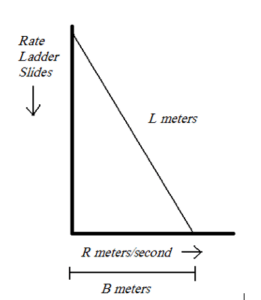
b. The moment we see a right triangle, we use the Pythagorean theorem
c.![]()
d. we are looking for dy/dt
3. Differentiate with respect to t:
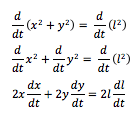
We should automatically see at this point that since l is constant, dl/dt is 0. I will leave it for a few steps for purpose of demonstration
4. We can now substitute in what we have.
a. We know dx/dt = r, dl/dt = 0, and x = b
![]()
![]()
b. We know also know y from the original Pythagorean theorem.
![]() which are all known quantities.
which are all known quantities.
![]()
Related Rate Example Problems
Volume questions are quite common examples of Related Rate Problems.
A spherical balloon is being inflated so that its volume increases at a rate of 20 cm3/s. How fast is the radius of the balloon changing when the radius is 10 cm?
Solution:
1. Identify Variables:
Volume
Radius
2. Governing Equations
![]()
3. We differentiate both sides with respect to time.
![]()
4. Substitute in the known rates quantities
![]()
5. Solve for wanted rate of change or quantity
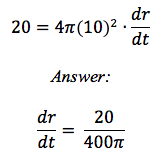
Another similar practice problem:
A spherical balloon’s area is increasing at the constant rate of 5 cm/sec. How fast is the volume increasing when the radius is 10 cm?
Solution:
This is a two-part question.
First we compute change in r, and then computer the equivalent change in V.
Let’s use the same series of steps as before:
Part 1:
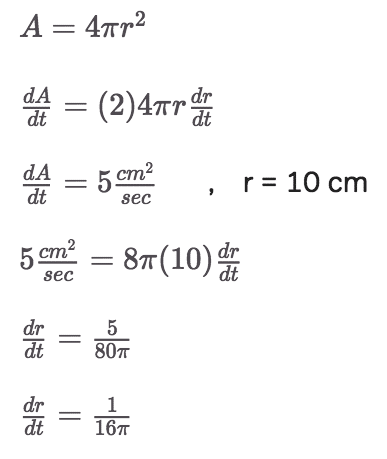
Part 2:
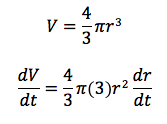
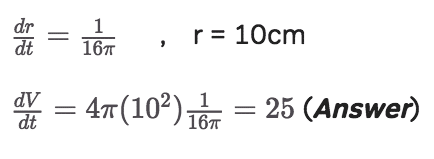





Leave a Reply