One thing that sets the AP Calculus BC exam apart from the AB exam is the topic of vector-valued functions. The BC test has them, while the AB does not. In this article we will review how to graph, find derivatives and integrals, and interpret the meaning of vector-valued functions.
What are Vector-Valued Functions?
A vector-valued function is like a typical function y = f(x), except that there is more than one output value. In fact, a vector may be thought of as a list of multiple values, such as (1, 4, -2).
On the AP Calculus BC exam, you will only encounter vector-valued functions having two outputs. You will see these as a pair of functions, x = f(t) and y = g(t), or equivalently, (f(t), g(t)).
For example, (3 cos t, 5 sin t) is a vector-valued function. It specifies the x-value (3 cos t) and y-value (5 sin t) for any given input t.
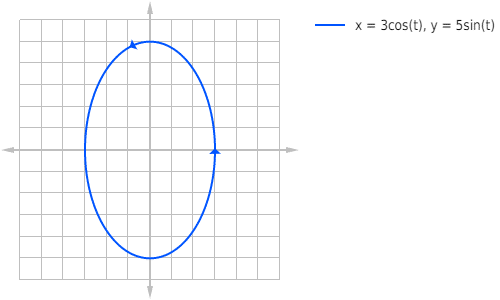
When there is a single input variable (like t in the above example), then a vector-valued function is essentially the same thing as a set of parametric equations.
Both of these concepts are basic types of multivariable functions. Check out AP Calculus Review: Multivariables for more.
Graphing
Let’s take a closer look at the example given above, (3 cos t, 5 sin t). How do you graph it?
Well what I did to create the graph shown above was to use graphing software.
In fact, most graphing calculators are capable of graphing vector functions. However, this feature will most likely be under term parametric. Here is a good parametric graphing tutorial.
However what do you do on the parts of the exam that do not permit a calculator?
Sketching the Graph Without a Calculator
Most often you will not need a detailed graph to answer any particular question. However, it’s good to have a few techniques up your sleeve to help you visualize a vector function when you need to.
Some situations come up so often that you should probably memorize them.
- For positive constants a and b, (a cos t, b sin t) is an ellipse. If a = b, then it’s a circle of radius r = a.
- Suppose f is any function. Then (t, f(t)) produces exactly the same graph as y = f(x). The only difference is that (t, f(t)) is a vector function, so all the methods that make sense for vector functions would work on this one.
More generally, if you need to know something about the graph of (f(t), g(t)), then you could choose a few sample points for t and plot the corresponding (x, y) pairs.
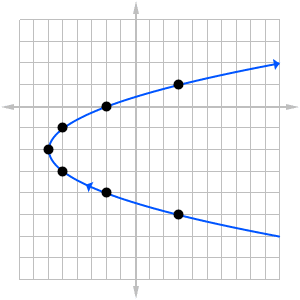
For example, to sketch (t2 – 6, t – 2) by hand, first create a table of values. Then plot the points and connect with a smooth curve.
| t | x = t2 – 6 |
y = t – 2 |
Point |
|---|---|---|---|
| -3 | 3 | -5 | (3, -5) |
| -2 | -2 | -4 | (-2, -4) |
| -1 | -5 | -3 | (-5, -3) |
| 0 | -6 | -2 | (-6, -2) |
| 1 | -5 | -1 | (-5, -1) |
| 2 | -2 | 0 | (-2, 0) |
| 3 | 3 | 1 | (3, 1) |
This graph is a parabola opening sideways to the right. The arrowhead on the curve indicates the direction of increasing t.
Derivatives
Just as you can take derivatives of regular (non-vector) functions, you can take derivatives of vector functions too. In fact, it’s easy! Just take the derivative of each component function separately, and keep your answer in the form of a vector.
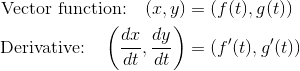
For example, the derivative of the vector function (t2 – 6, t – 2) is (2t, 1).
In the next section, we’ll see what the derivative can tell you about the motion of an object described by a vector-valued function.
Position, Velocity, and Acceleration
Remember that if s(t) is the position function for an object moving along a straight line, then you can find the object’s velocity and acceleration by taking derivatives.
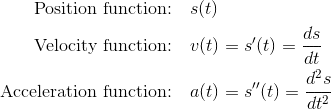
In a similar way, if the vector function (f(t), g(t)) defines the position of an object in terms of time t, then its velocity and acceleration (as vector functions) can also be found by taking derivatives:
![]()
In any case, whether talking about single-variable functions or vector-valued functions, the velocity involves the first derivative while the acceleration vector involves the second.
Example – Velocity Vector
If a particle moves in a the xy-plane so that at time t > 0 its position vector is
, then its velocity vector at time t = 3 is
- A. (ln 6, ln 27)
- B. (ln 9, ln 27)
- C. (6e9, -27e-27)
- D. (9e9, -27e-27)
Solution
From what we have already discussed, velocity is the first derivative of position. Therefore, being very careful with the Chain Rule, we find:
![]()
Then after plugging in the given time t = 3, we get:
![]()
The correct choice is C.
Length of a Curve and Distance
Although we typically think of parametric curves when talking about curve length, the same formula works just as well for vector-valued functions.
In fact, the length formula gives you the total distance of a particle traveling along a vector function (f(t), g(t)) from time t = a to t = b.
![]()
Example – Distance
A particle moves along a path described by
. Find the distance that the particle travels along the path from t = 0 to t = π/2.
(Assume that calculators are allowed.)
Solution
This is a straightforward application of the length integral. Use your calculator once you have set up the formula correctly.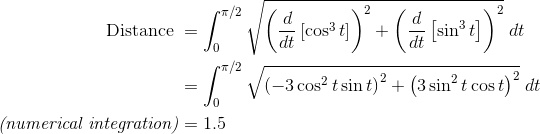
Summary
Vector-valued functions are an important part of the AP Calculus BC exam. You should know how to:
- Graph and interpret the graph of a vector-valued function.
- Find derivatives and use them in particle motion problems.
- Use the curve length formula.
For a complete list of topics found on the BC exam, check out What Topics are on the AP Calculus BC Exam?.




Leave a Reply