What are multivariables, and what are they doing on the AP Calculus test? In this short review article you’ll discover what you need to know about multivariables for the AP Calculus BC exam!
The AP Calculus Exams and Multivariables
By definition, a multivariable function is simply a function that has more than one (multiple) input and/or output variable. Happily, the only kinds of multivariable functions you might encounter on the test are those with one input — t — and two outputs — x and y — often called parametric or vector functions.
Moreover, multivariables only make an appearance on the AP Calculus BC exam, not the AB. (For a complete list of topics found on the BC exam, check out What Topics are on the AP Calculus BC Exam?)
Parametric and Vector Functions
How do we track the motion of a rocket as it blasts off from the surface of the Earth? We must keep track of many different things. For each instant of time, t, the rocket will be at some horizontal distance, x = f(t) away from the station. But the height also changes with time according to a separate function, y = g(t).

A parametric function is a set of two (or more) functions all defined in terms of the same parameter (usually t for time). We usually express a parametric function as a list, x = f(t), y = g(t).
A vector function is the same concept except in the form of a vector: (f(t), g(t)).
Example
Here is a typical parametric function:
![]()
And the same expression written as a vector function:
![]()
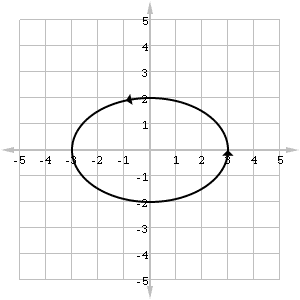
Both of the above functions have the same graph, which is an ellipse. Most graphing calculators are capable of graphing parametric functions.
Derivatives of Parametric Functions
If x = f(t) and y = g(t) define a parametric function, then we find the derivative by the formula,
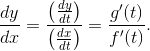
Example
Find the slope of the ellipse (3 cos t, 2 sin t) at t = π/3.
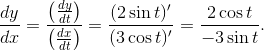
Plugging in the given t = π/3,
![]()
Velocity and Acceleration Vectors
If (f(t), g(t)) define the position of an object in terms of time t, then the following expressions define the velocity and acceleration vectors of the function at time t.
![]()
Note that the velocity vector involves the first derivatives while the acceleration vector involves second derivatives.
Example
With our running example, the ellipse equations, we can derive expressions for the velocity and acceleration of an object traveling along the ellipse.
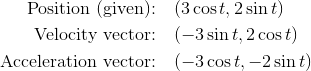
Length of Parametric Curves
The formula for the length of a parametric curve x = f(t) and y = g(t) from t = a to t = b is:
![]()
Example
Set up the formula for the length of the semi-ellipse defined by (3 cos t, 2 sin t) where 0 ≤ t ≤ π.
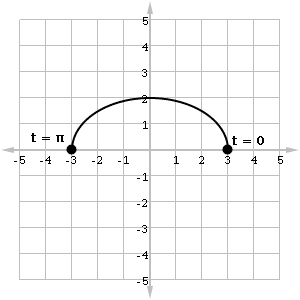
Using the formula for the length of a curve:
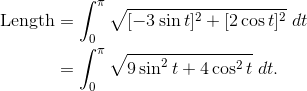
Summary
Multivariables only show up on the AP Calculus BC exam, and only in the form of parametric or vector functions. The topics you should be aware of include:
- Graphing and interpreting graphs of parametric functions
- Finding the slope of a parametric function at a given point
- Finding velocity and acceleration vectors
- Computing the length of a parametric curve





Leave a Reply