The AP Calculus exams include a substantial amount of integration. So it’s very important to be familiar with integrals, numerous integration methods, and the interpretations and applications of integration. In this short article, we’ll take a look at some of the most common integrals on the test.
For a quick review of integration (or, antidifferentiation), you might want to check out the following articles first.
And now, without further ado, here are some of the most common integrals found on the AP Calculus exams!
Common Integrals
The following seven integrals (or their close cousins) seem to pop up all the time on the AP Calculus AB and BC exams.
1. Remember your Trig Integrals!
Trigonometric functions are popular on the exam!
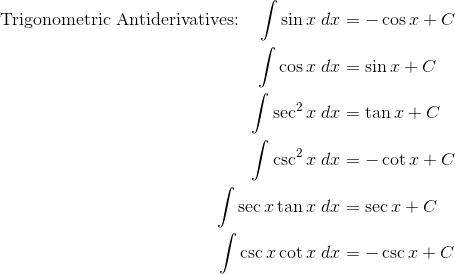
2. Simple Substitutions
You need to recognize when to use the substitution u = kx, for constant k. This substitution generates a factor of 1/k because du = k dx.
For example,
![]()
3. Common Integration By Parts
Integrands of the form x f(x) often lend themselves to integration by parts (IBP).
In the following integral, let u = x and dv = sin x dx, and use IBP.
![]()
4. Linear Denominators
Integrands of the form a/(bx + c) pop up as a result of partial fractions decomposition. (See AP Calculus BC Review: Partial Fractions). While partial fractions is a BC test topic, it’s not rare to see an integral with linear denominator showing up in the AB test as well.
The key is that substituting u = bx + c (and du = b dx) turns the integrand into a constant times 1/u. Let’s see how this works in general. Keep in mind that a, b, and c must be constants in order to use this rule.
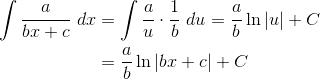
5. Integral of Ln x
The antiderivative of f(x) = ln x is interesting. You have to use a tricky integration by parts.
Let u = ln x, and dv = dx.
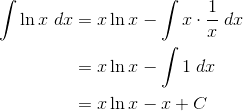
By the way, this trick works for other inverse functions too, such as the inverse trig functions, arcsin x, arccos x, and arctan x. For example,
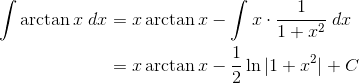
6. Using Trig Identities
For some trigonometric integrals, you have to rewrite the integrand in an equivalent way. In other words, use a trig identity before integrating. One of the most popular (and useful) techniques is the half-angle identity.
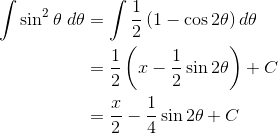
7. Trigonometric Substitution
It’s no secret that the AP Calculus exams consist of challenging problems. Perhaps the most challenging integrals are those that require a trigonometric substitution.
The table below summarizes the trigonometric substitutions.
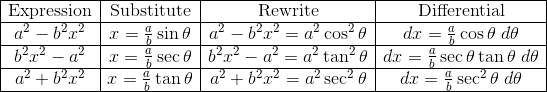
For example, find the integral: ![]()
Here, the best substitution would be x = (3/2) sin θ.
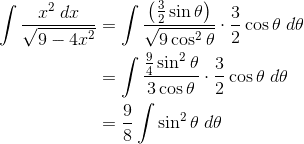
Now we’re not out of the woods yet. Use the half-angle identity (see point 6 above). We also get to use the double-angle identity for sine in the second line.
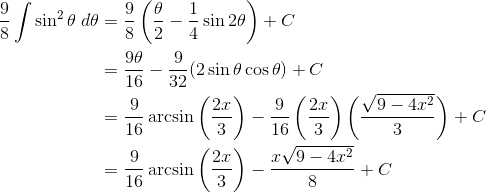
Note, the third line may seem like it comes out of nowhere. But it’s based on the substitution and a right triangle.
If x = (3/2) sin θ, then sin θ = (2x) / 3. Draw a right triangle with angle θ, opposite side 2x, and hypotenuse 3.
By the Pythagorean Theorem, we find the adjacent side is equal to: ![]()
That allows us to identify cos θ in the expression (adjacent over hypotenuse).
Finally, θ by itself is equal to arcsin(2x/3).




Leave a Reply