AP Calculus BC Review: Partial Fractions

The Method of Partial Fractions is actually a technique of algebra that allows you to rewrite certain kinds of rational expressions in a more useful way.

In this review, we will discuss the how and when to use the method in integral problems, especially those found on the AP Calculus BC exam.

The Method of Partial Fractions (PF)

The method is actually the reverse of adding rational expressions.

Suppose you have a rational function, that is, a fractional expression of two polynomial.

More precisely, every rational function has the form , where both the numerator f and denominator g are polynomials.

The question is this: Can we find two or more simpler rational expressions that add to the given one?

The key is to factor the denominator. The denominators of the new fractions will involve these factors. Then, working backward, you can figure out what the new numerators must be in order to arrive at your given function.

Of course, there are many details that I’m leaving out at the moment. We’ll explore the method in more detail below.

PF for Non-Repeating Linear Factors

First, PF only works when the degree of the denominator is greater than the degree of the numerator. If the numerator has higher degree than the denominator, then you must first do polynomial (or synthetic) division. I have yet to see a problem on the Calculus BC exam that requires polynomial division, so we’ll skip over that in this review.

Furthermore, on the AP Calculus BC exam, you will only need to know about denominators that factor into non-repeating linear factors.

In other words, the denominator will factor completely into unique factors:

The next step after factoring is to write down as many fractions as you have factors. We know what the denominators will be (those are the factors themselves). But we don’t know the numerators yet. For now, just write the numerators as variables. We’ll have to solve for them later.

Next you’ll need to figure out exactly what those numbers are on top, A₁, …, A_n. By the way, when there are only two or three factors, I usually call these numbers A, B, C, etc. The actual variable name doesn’t matter.

Although there is no calculus involved at this step, this is where a lot of students seem to get stuck. The algebra can be very tricky and tedious. So I’ll explain it using two different methods on the same example.

Finally, integrate each term separately. When the factors are fractions with a linear denominator, you can expect the antiderivative to involve natural logarithms.

Example Using Partial Fractions

Find the antiderivative.

Decomposing the Expression

First, check the degree of the top and bottom. Since the denominator has degree 2 while the numerator has degree 1, we may use PF.

The method always begins with factoring the denominator. Sometimes this step is already done in a given problem on the BC exam, but not always.

Now since there are two factors, there will be two separate fractions. Let’s let A and B stand for the unknown numerators.

From here, there are two ways to go.

Method #1 — Recombine Fractions

The idea is that we want the sum of the fractions to equal the original rational expression. So use your algebra skills to recombine the fractions and compare the results.

You’ll need a common denominator, but that’s the easy part! You just have to multiply the two denominators back together.

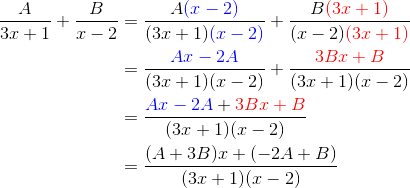
So, after grouping like terms, we set the numerators equal to one another. Comparing the x-terms and constant terms, this leads to a system of two equations.

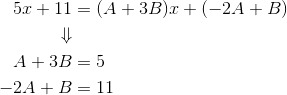
Now there is a variety of ways to solve such systems. Matrix methods work, if you know how to use them.

Alternatively, you could do simple substitution.

Solve the first equation for A, to get: A = 5 – 3B. Then plug in that expression for A in the second equation and solve for B.

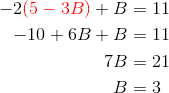
Finally solve for A by plugging in the known B-value. A = 5 – 3(3) = -4.

Therefore, we now have a partial fractions decomposition for the original rational expression.

Surely this is the end of the process right? Well no, you still have to integrate the decomposed form. (We’ll do that eventually.)

But before getting to that, let’s discuss other methods for decomposing the fraction which is more efficient than this one.

Method #2 — Heaviside Cover-Up Method

The Heaviside Cover-Up Method avoids all that algebra, but seems more like a “trick.” It’s guaranteed to work for non-repeated linear factors, but the reason it works is kind of subtle.

Here’s how you do it.

For each factor, first find it’s root, that is, the value of x that results when you set it equal to zero and solve.

Then cover up that factor in the original rational expression, and plug the root into x everywhere else you see it in the expression.

Evaluate it, and this will be the A_i (numerator) value in the PF decomposition.

Going back to our example, remember we factored and decomposed the function so that:

The first factor is 3x + 1. Setting it equal to zero and solving, we get:

Now we plug this value back into the original expression, but ignore the factor (3x + 1).

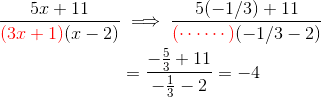
This tells us that A = -4.

Then move on to the second factor, (x – 2), whose root is x = 2. Ignore that factor now and plug in.

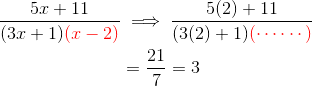
Now we have B = 3.

The end result is the same as with Method #1, but it takes far less time.

Final Step: Integrate!

After completing either the algebraic method or Heaviside Cover-Up, you would now be in position to find the antiderivative.

Just be careful: There are usually simple u-substitutions that must be made in order to get the right answers.

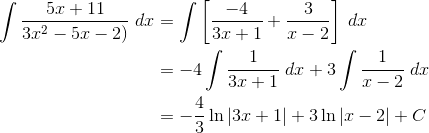
Conclusion

Though at first it may seem as though Partial Fractions is difficult, it’s more like the challenge of learning to ride a bike.

At first you don’t know what you’re doing and you might fall down a lot. But with enough practice, and especially the willingness to get back on the bike after falling off, then you’ve learned a skill that will stay with you for the rest of your life!

In fact, similar to riding a bike, I think that PF is kinda fun. (But my close friends assure me that I’m just weird.)

Check out the following resource for other important integration technques: AP Calculus Review: Indefinite Integrals.