AP Calculus BC Review: Integration By Parts

Integration by Parts (or IBP) is a powerful method for integrating certain kinds of products. This technique is just one tool in your toolbox, but it’s essential to master it if you want to maximize your score on the AP Calculus BC exam.

In this post, we’ll see the statement of the IBP formula, a short proof showing why it works, and a number of examples.

Method of Integration by Parts

Suppose u and v are differentiable functions of x. Then the IBP formula states that:

The formula works as follows.

1. Given an integral of the form on the left, identify two parts, u and dv. Here, u is a function of x, while dv is a function involving dx as well (which is called a differential).
2. Differentiate u. More precisely, you should find the differential, du.
3. Integrate dv to get a function v of the variable x.
4. Now put together the formula on the right side of the equals sign, involving u, v, and du.
5. Finally, work out the new integral. That is, find the integral of v du.

Why Does It Work?

Although you will not need to derive or prove the IBP formula on an AP Calculus exam, it may help your understanding in general to see the proof.

IBP is really just the Product Rule in reverse.

First of all, the IBP formula may be rewritten in the following way. Let u = f(x) and v = g(x). Therefore, we have dv = g '(x) dx. Then the formula takes the form:

Written in this way, it should be clearer how the Product Rule comes into the picture. But here are the details.

Starting with the statement of the product rule, integrate both sides. Then solve for one of the two integrals.

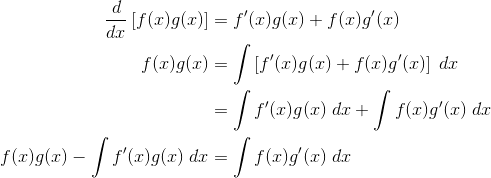
As you can see, the last line is precisely the IBP formula.

What Should I Chose?

The effectiveness of IBP relies on a judicious choice of u and dv. The right choice simplifies the integral, while the wrong choice may get you hopelessly lost in a sea of complication.

Generally speaking, the choice for u should be easy to differentiate and hopefully get simpler upon differentiation.

Then dv will consist of the remaining factor(s) together with the differential dx. This part must be something easy to integrate, because you will need to produce the antiderivative v rather quickly.

With experience, you may pick up on a few patterns.

Often u tends to be a polynomial, logarithm, or inverse trig function. On the other hand, dv typically involves exponentials or trigonometric functions.

Examples

Now let’s see if we can put the theory to the test. All of the integrals below have a similar level to those on the AP Calculus BC exam. They all require IBP. But keep in mind, on the test you will not have the luxury of knowing which method is the best one to use for any given integral.

Example 1 — Simple IBP

Solution

This is exactly the right situation in which IBP is very effective. But you have to choose u and dv wisely.

Following the general advice above, perhaps u = x (polynomial) and dv = e^5x dx (exponential).

Note, when we find v, there will be a substitution for the 5x.

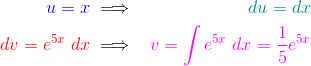
For this example, I’ve color-coded the parts to make it easier to see where everything goes in the IBP formula. As before, there’s going to be another substitution step in the integral of e^5x.

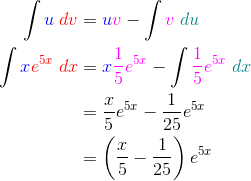
Example 2 — Logarithms

Solution

This time we should let u = ln x. This is because it is much easier to take the derivative of ln x than to take its antiderivative.

This forces dv to be x² dx. Now we need to find du and v.

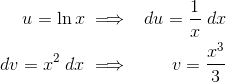
Then plug everything into the IBP formula and solve it completely.

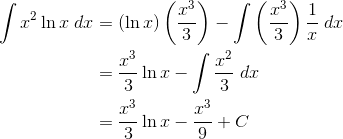
Example 3 — Multiple IBP

Solution

Here the correct choice is u = x² and dv = cos x, but as we shall see, the IBP formula will not lead to a final answer — at least not immediately…

We’ll have to use the integration by parts more than once in this example.

First, start the process as in the previous examples.

A single application of the method yields:

However, this time we can’t easily finish the integration step. In fact, the resulting integral still has the form of a product. Time for a second application of IBP.

Let’s work on that second integral separately. This time we will have:

Therefore,

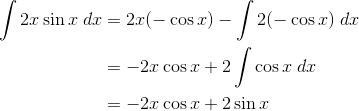
But don’t forget, this is just part of the final answer. Let’s put this result together with what we’ve already done.

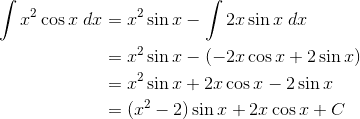
Finally we have arrived at the answer to this problem!

Other Techniques

Integration by parts is just one of the many tools available for finding antiderivatives that you’ll need to know for the AP Calculus BC exam.

For example, you’ll also need to know how to do the following.

• u-Substitution (if you’re rusty on this one, you might want to check out: AP Calculus BC Review: Integration By Substitution)
• Partial fractions
• Advanced trigonometric substitutions

In fact, many integration problems require the use of multiple techniques. And of course, you’ll have to know all of the basic antiderivative rules as well.

For a more comprehensive review of the various integration techniques, check out: AP Calculus Review: Indefinite Integrals