One complaint of some folks studying for the GMAT is: “I know a good deal of math. I could do most of the math problems on the GMAT if I had enough time, but I often don’t see the quick ways to do these problems. How do I see the shortcuts?” This post is an attempt to answer this question. First, three wickedly challenging GMAT math problems. Give yourself a strict 90 second time limit for each.
1) A series is defined, for positive integer n, by
What is the sum of the first 60 terms of this series?
(A) 1/6
(B) 1/3
(C) 29/30
(D) 40/63
(E) 61/63
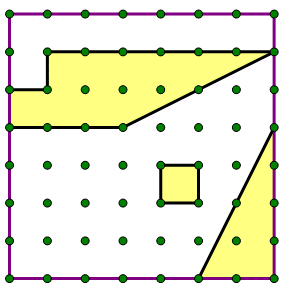
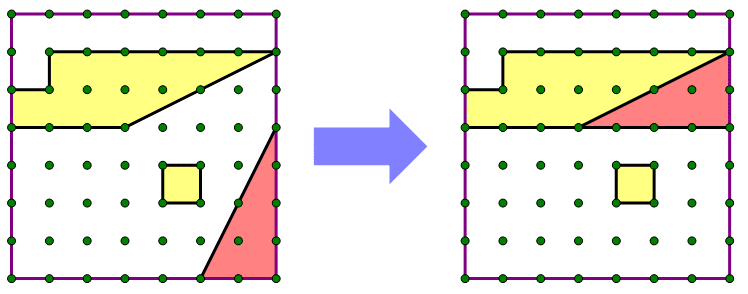
2) The big outside purple square above has an area of 84, and the dots are all equal spaced, forming smaller squares. What is the sum of the areas of the shaded yellow regions?
(A) 20
(B) 24
(C) 28
(D) 32
(E) 36
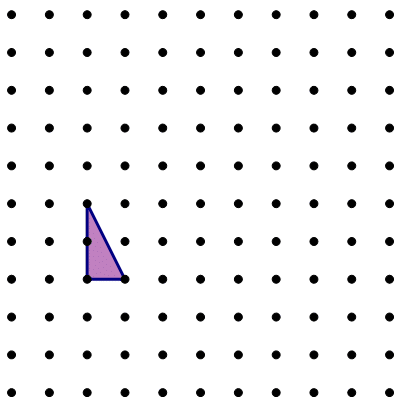
3) The above 11 x 11 grid of dots is evenly spaced: each dot is separated by one unit, vertically or horizontally, from its nearest neighbors. Drawn in the diagram is a single right triangle with legs of length 2 & 1. How many right triangles, congruent to this one, of any orientation, can be formed by three dots from this grid
(A) 360
(B) 480
(C) 600
(D) 720
(E) 3600
Good at math but …
Some folks are really rusty at math, and need to learn, or re-learn, the basic rules. There’s no substitute for the hard work of review and practice problems. This post is not primarily for these folks, although they may have some insights from what follows.
Other folks have a reasonably good grasp of the basic rules, but many problems, such as the ones above, take them a long time. These folks can see the long, plodding, tedious solutions, but then they are frustrated when they read about the lightning-fast shortcut in the solutions. “How was I supposed to see that approach?” they ask, with great frustration. This article is an attempt to address this frustration.
The brain
The uppermost layer of the human brain is a truly miraculous piece of equipment called the cerebral cortex. The cerebral cortex is divided down the middle into two hemispheres—the right & left hemispheres, which control different skills and different types of thinking. Colloquially, folks refer to these as the “right brain” and the “left brain.”
Each hemisphere controls motion & sensation on the opposite (e.g. contralateral) side of the body: when you raise your right thumb, see with your right eye, or extend your right leg, that process is controlled by the left-brain. While there are many exceptions, as a very rough general rule, folks who are right-handed tend to be left-brain dominant, and the lefties tend to be right-brain dominant. What happens in these two hemispheres?
In addition to controlling the right side of the body, the left brain operates via logic and organization. The left-brain is rigid, precise, linear, and organized. The left-brain is very good at following exact rules and procedures. The left-brain is reductionist: understanding the whole by understanding each part. The left-brain excels at differentiation: drawing a fine distinction between two closely related things. The left brain governs grammar and syntax —what you might call the “mathematical” side of language. If I say, “He are a good friend of I“, your left-brain tells you that this sentence has serious problems.
The right-brain, sometimes called the “artistic brain” is very different. We dream with our right-brains. The right-brain understands art, poetry, metaphor, myth, and symbols. The right-brain is at home with images and non-linear associative processes. Imagination, intuition, and most “out of the box” thinking are closely associated with the right-brain. The right-brain is holistic: seeing the whole that emerges from and transcends the sum of the parts. The right-brain excels at integration: seeing the larger connecting principles that unite apparently unconnected elements. The right-brain is the world’s best pattern-matching machine, better than any computer at tasks such as: facial recognition, voice recognition, map reading, etc. The right-brain also processes language, but a very different side of language. Imagine if Person #1 says, “This is a great situation!” in a voice radiating innocent joy and optimism; imagine Person #2 says, “This is a great situation!” in a voice dripping with cynicism and bitter sarcasm. According to the left-brain, those two people said exactly the same thing (same grammar, same syntax, etc.) It’s only the right brain that hears this kind of difference: emotional inflection, intonation, emphasis, non-verbal communication, body language, etc. etc. The right-brain is all about the subtleties of context.
Your brain and math
Folks who are extremely left-brain dominant were typically the “good at math” students in school. Give these people a recipe, a procedure, a set of precise rules, and they can follow it again and again, keeping every detail organized. This is usually enough to garner good grades throughout most high school math.
Meanwhile, folks who are extremely right-brain typically found school-math more challenging. Often these folks would get all the big ideas, but they couldn’t apply them. They could sometimes make incredible leaps of intuition that left their left-brain friends simply scratching their heads, but more often the right-brain folks lose track of details, get disorganized, and can’t consistently produce correct answers.
Naively, it would seem that the left-brain is the “math brain”, and in the simple world of cookie-cutter school math, that’s largely true. BUT, success in mathematics in the broadest sense, like success in most anything, draws on both sides of the brain. Those individuals who are exceptionally well-developed in both halves of the brain, folks such as Leonardo da Vinci and Johann Wolfgang von Goethe, are often regarded as among the smartest folks ever to walk the planet. Even Isaac Newton, that left-brain superstar, had enough right-brain intelligence going on to see that that an apple’s fall and the Moon’s orbit were corresponding parts of a grand all-encompassing pattern known as Gravitation.
Most intelligent folks have some balance of left-brain and right-brain skills, but many people lean much more heavily to one side than to the other, and some folks are almost 100% in one direction or another.
If you’re an extreme right-brain artsy person, you need to practice, practice, practice. In order to develop your left-brain logic, you need to practice organization, strict procedures, and precise detail management — all, in the most methodical way possible. You need to get in touch with your inner anal-retentive bookkeeper. There’s no glamorous shortcut. There’s no substitute for the hard work of assiduous nitty-gritty practice.
But, what if you’re an extreme left-brain person? You already can organize things, manage details, and follow precise recipes and procedures to a T. You have no problem identifying the straightforward logical rule-based solution to a problem, but sometimes that slow plodding method would take 10+ minutes in a GMAT Quant problem. How do you make the leap from this slow & steady method to the lightning-fast, insight-based, Leonardo da Vinci solution?
Seeing the Leonardo da Vinci solution
For the extreme right-brain person, getting in touch with the left-brain involves following some rules and recipes — what the left-brain folks love and what the right-brain folks have always chafed against. Of course, what the left-brain folks would love is some kind of logical, linear plan for getting in touch with the skills of the right-brain. That’s what they would love, and of course, that’s impossible.
How does an extreme left-brain person develop right-brain skills? Well, not surprisingly, entering that non-linear world is a non-linear process. Here are some suggestions. Notice visual patterns, looking for symmetries (wall paper, tile patterns, etc.). Read poetry. Study song lyrics, including the lyrics of highly associative and evocative songs (e.g. “A Hard Rain’s a-Gonna Fall“, “I am the Walrus“, “Stairway to Heaven“, “Mysterious Ways“, “Losing My Religion“, etc.) Play with visual & spatial puzzles—one of my favorites is the SOMA cube. Start keeping a journal of your dreams.
Look at art, but really look! What do I mean? Take any masterpiece — for example, the Mona Lisa. If you look at that, your left-brain takes about half a second to say, “Yes, I know that. OK, I’m done.” The right-brain takes more time to feel into the image. Take a masterpiece, and set a stop-watch, say for 10 minutes, and simply stare at the art for that time. For the left-brain, 10 minutes will feel like an eternity. You have to put your logical, analytical mind on hold and simply allow the image to work its magic on you. Once, I had the opportunity to stare at the Mona Lisa for a good 10-15 minutes, and I swear, as I stood there, every single human emotion ran across that iconic face. All of this is “calisthenics” for your right-brain.
On the GMAT, keep a journal of any math problems you solve using a long formula-based approach but which have a much shorter insight-based solution, especially with the most common GMAT questions. This may begin with one or more of the problems at the top of the page. For the purposes of your GMAT practice, if you do such a problem the long methodical way, and the solution shows a much shorter way, consider this a question that you got wrong, regardless of whether you found the correct answer. You need to hold yourself to a new standard. For example, estimation is a great right-brain math skill that will help you on the GMAT. For each question like this, write down in your journal the nature of the insight on which the solution was based — by forcing yourself to articulate the insight each time, you will be creating important links between your left- and right-brains.
All of this can be hard work for an extreme left-brain person, but it will pay off in huge dividends, on the GMAT and beyond. Extreme left-brain thinkers are good at obediently following other people’s rules, but it takes some right-brain intuition and insight to be a visionary leader, especially in a post-industrially electronically driven marketplace that is in constant evolution!
Still struggling to finish the quantitative section on time? Learn about GMAT timing strategy in our Ultimate GMAT Pacing Guide!
Summary
If anything I said in this article triggered an “aha!” for you, you might want to take another look at the problems above before reading the solutions below. Here’s another math problem that invites an insight-based approach, from inside Magoosh:
4) http://gmat.magoosh.com/questions/100
If you would like to add any thoughts of your own, or ask questions, please let us know in the comments section below. Thanks!
Practice problem solutions
1) Think about the first few terms and last few terms in this pattern. Don’t simplify any of the individual terms — just look at the list, to notice the pattern.
Notice that the second, negative term of any one line is the same as the first, positive term of the previous line. These will cancel when we find the sum. When we add all the terms, the positive (2/4) in the first line will cancel with the negative (2/4) in the second line; the positive (3/5) in the second line will cancel with the negative (3/5) in the third line; and so forth in that pattern, up until the positive (60/62) in the 59th line cancels with the negative (60/62) in the 60th line. Thus, everything in the series cancels except for the negative (1/3) in the first line and the positive (61/63) in the 60th line — that’s the sum we need to find. Remember, to subtract fractions, we find the common denominator.
Answer = D
2) In this problem, the dots break the big square into 7 x 7 of the little squares. Each little square would have an area of 84/49 = 12/7. We could spend a great deal of time figuring out the areas of the three individual irregular shapes — all of which will be ugly fractions — and then add them. That could take 15 minutes.
Instead, let’s re-arrange. First, flip that triangle around to fit neatly into that slanted place:
Now, take the little square, and stick it in that square notch in the upper left.
The combination of those areas simply occupies two of the seven rows — in other words, 2/7 of the whole square. (When you multiply the fraction, remember to cancel before you multiply!)
Answer = B
3) This is a hard problem, and as with many counting problems, solving it elegantly requires framing the problem well.
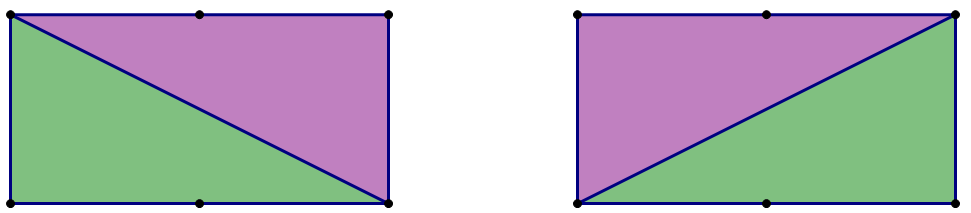
Every one of those triangles will fit in a 1 x 2 rectangle, which could be oriented with the longer dimension either vertical or horizontal. Let’s focus on the horizontal ones first. One 1 x 2 rectangle will hold four possible triangles:
So, one 2 x 1 rectangle is the equivalent of four of the triangles we want. How many of these rectangles will fit across a row?
Well, a 2 x 1 rectangle, oriented horizontally, has a left square and right square. The left square could occupy squares #1 – #9 in the row, so there are nine possible 2 x 1 rectangles in a row.
Overall, (four triangles in a 2 x 1 rectangle) times (9 rectangles in a row) times (10 rows) = 4 x 9 x 10 = 360 triangles oriented with the long leg horizontal.
Of course, for the rest of the triangles, the ones with the long leg oriented vertically, everything will be exactly the same — vertical rectangles, 9 rectangles in a column, 10 columns — so there are 360 of these triangles as well, for a total of 360 + 360 = 720.
Answer = D

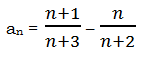
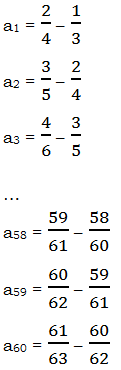
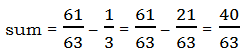

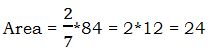






Leave a Reply