Here are a few 800+ counting problems.  Yes, that’s right, 800+, which means, as hard as (or possibly harder than) anything you will see on the GMAT.  If you can do these, you are in great shape!

1) How many four digit numbers have no repeat digits, do not contain zero, and have a sum of digits equal to 28?

A. 14

B. 24

C. 28

D. 48

E. 96

2) How many distinct four-digit numbers can be formed by the digits {1, 2, 3, 4, 5, 5, 6, 6}?

A. 280

B. 360

C. 486

D. 560

E. 606

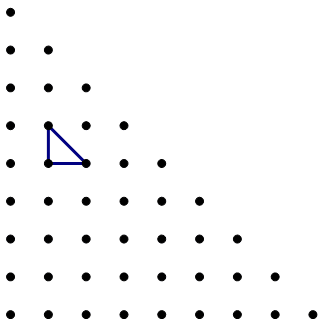
3) In the grid of dots above, each dot has equal vertical & horizontal spacing from the others.   A small 45-45-90 triangle is drawn.  Counting this triangle, how many triangles congruent to this one, of any orientation, can be constructed from dots in this grid?

A. 112

B. 120

C. 240

D. 448

E. 480

4) Fifteen dots are evenly spaced on the circumference of a circle.  How many combinations of three dots can we pick from these 15 that do not form an equilateral triangle?

A. 160

B. 450

C. 910

D. 1360

E. 2640

Solutions will come at the end of this article.

Basic ideas of counting

The most basic of all ideas in counting is the Fundamental Counting Principle.   This is more conveniently stated in words than as a formula, so formula-based studiers often overlook the importance of this idea, to their own detriment.   The more familiar counting ideas — more familiar because they have formulas associated with them!! — are permutations and combinations.  It’s important to recognize: all the ideas & formulas concerning permutations & combinations can be derived directly from the FCP, and in fact, often in the case of permutations, it’s much simpler to use the FCP directly than to use any permutation formula.

Not so basic …

Those are the basic ideas.  They are relatively easy to state, and they are explained in the posts at those links.   The problem is: when you read an individual counting problem, how do you know which rule to use?

That’s precisely the hard part of counting, and what’s frustrating is that there’s not a simple flowchart/procedure we can recommend that will work for all counting problems.  The hardest thing about any counting problem is knowing how to begin, and essentially, this a right-brain pattern-matching procedure.  In the post How do to GMAT Math Faster, I discuss left-brain vs. right brain thinking in greater depth.   The gist is: any left-brain skill or procedure can be diagrammed and clearly explained in a logical step-by-step way, but any right-brain process is an inherently non-linear process into which one has to grow slowly, through experience.

Of course, in problem solutions, you can read about how they solved the problem, but this is tricky.    You see, in any counting problem, often the hardest part is how one initially perceives and dissects the situation, the way one breaks it into steps or stages.   Once that perceptual choice is made, especially if it’s a good choice, then applying any rules or formulas is easy.   If you just scan the solution for formulas & rules, you will say, yes, when we look it this way, of course we do that calculation.   That’s not what you need to study.  Above all, you need to study the very beginning: what was the very choice the solution made in solving the problem?  How did they begin the problem?  How did they frame the situation?  What were their perceptual choices?    Left-brain thinkers always want to know what to do, but in the right-brain realm, the most important choice is how to see, and once you are seeing things in the right way, it’s obvious what to do.  That’s especially what left-brain thinkers need to get from the solutions to counting problems.   Patterns emerge over time, and those initial perceptual choices become more and more natural.
Here are a few concrete recommendations:

1) Don’t just memorize the permutation & combinations formulas.  Memorization is not understanding.   Understand the FCP, and understand how that more fundamental idea underlies the formulas & procedures of permutations & combinations.   Those are the basic tools you need to know very well.

2) In counting problems, whether you get the problem right or wrong, always read the solutions.  Again, you are looking for how the solution began, the very first perceptual choice made before any calculations were done.  If you are more of a left-brain person, I actually would recommend keeping notes of the situation given in the question and the first few steps, the perceptual choices, made in the solution.   Forcing yourself to articulate the choices will help to build connections between the brain’s two hemispheres.

3) See the How do to GMAT Math Faster article for more tips on how to exercise and develop your right-brain.

Summary

If you had trouble with the questions above, it may be that some of the information in this article or at one of the linked articles gives you a clue, but most likely you will have to study the solutions below.  Remember to be mindful of what you need to get from the solution to a counting problem, as discussed above.  Here’s another counting problem for more practice:

6. http://gmat.magoosh.com/questions/831

If you would like to share your experience of these problems or ask anything about what I’ve written, please leave a comment in the comment section.

Explanations for practice problems.

1) For those familiar with Kakuro, this problem presents a related challenge.  First, we need to know: how many combinations of four distinct single-digit numbers have a sum of 28?  Start with the three highest digits: 9 + 8 + 7 = 24, so {9, 8, 7, 4} is one such combination.  First, keep the 9 & 8, and bring the other two closer together: {9, 8, 6, 5}.  OK: that exhausts possibilities with 9 & 8 as the highest numbers.  Now, omit 8, and try 9 & 7: even with the largest available digits, 9 + 7 + 6 + 5 = 27, so this will not be big enough.  Similarly, without 9, even with the largest available digits, 8 + 7 + 6 + 5 = 26, also is not big enough.  If we omit either 9 or 8, the sum is not big enough, and with both 9 & 8, there are only two possibilities: {9, 8, 7, 4} or {9, 8, 6, 5}.   Thus, only two possible sets of four digits.

For each one of these, we could permutate the number in any order.  4! = 24, so for each of the two sets, there are 24 different four-digit numbers we could form.  That’s a total of 2*24 = 48 different four-digit numbers.

Answer = D

2) We will break the possible numbers into four different groups.  First, we will consider all the numbers with no repeat digits: how many different sets of four different number can I choose from the digits 1-6?  Remembering the tricks for calculating combinations, 6C4 = 6C2 = 15.  For each one of those, we can permutate the digits in any order: 4! = 24.   To multiply 15*24, use the doubling & halving trick.  Half of 24 is 12, and twice 15 is 30, so 15*24 = 30*12 = 360.  That’s group #1, all the four-digit numbers with four distinct digits.

Group #2 will be the group with two 6’s and the other two digits distinct.  Think about this.  There are 4C2 = 6 “slots” the two sixes could occupy:

6 6 _ _

6 _ 6 _

6 _ _ 6

_ 6 6 _

_ 6 _ 6

_ _ 6 6

Now, for each of those, use the FCP: we would pick five digits for the first empty slot (1, 2, 3, 4, 5), and that would leave us four choices for the second empty slot.  Thus, for each of those six, there are 20 four-digit numbers we could create. That’s 6*20 = 120 total in group #2.

Group #3 will be the group with two 5’s and the other two digits distinct.  Think about this.  For symmetry reasons, there must be exactly as many numbers in this group as there are in group #2.  There are 120 in this group.

Group #4 will have two 5’s and two 6’s constituting the four digits.   If we choose the two slots into which to drop the 5’s, the 6’s have to go into the other slots.  Therefore, there must be 4C2 = 6 of these.  Here they are: 5566, 5656, 5665, 6556, 6565, 6655.

The total is the sum across these four groups: 360 + 120 + 120 + 6 = 606

Answer = (E)

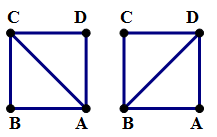
3) First, notice that in every square, we could construct four different triangle.

In the above square, we can construct triangles ABC, ACD, ABD, and BCD, all congruent.

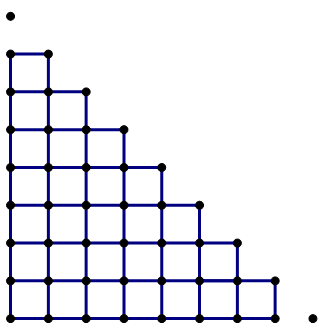
Well, if we take all the squares of this size in the diagram,

We have 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 squares.  That’s 28 squares, times four triangles in each square: 28*4 = 112.

BUT, we can’t forget to count the leftover triangles on the diagonal slant:

That’s 8 more triangles, for a total of 112 + 8 = 120

Answer = (B)

4) Well, first of all, ignoring the type of triangle formed, how many combinations total?  The easiest way to think about this is to use the Fundamental Counting Principle.   For the first dot, 15 choices, then 14 left for the second choice, then 13 left for the third choice: that’s 15*14*13.  But, that will count repeats: the same three dots could be chosen in any of their 3! = 6 orders, so we have to divide that number by 6.  (NOTICE the non-calculator math here).

(15*14*13)/6

Cancel the factor of 3 in 15 and 6

(5*14*13)/2

Cancel the factor of 2 in the 14 and 2

(5*7*13) = 5*91 = 455

That’s how many total triangles we could create.

Of these, how many are equilateral triangles?  Well, the only equilateral triangles would be three points equally spaced across the whole circle.  Suppose the points are numbers from 1 to 15.  From point 1 to point 6 is one-third of the circle — again, from point 6 to point 11, and from point 11 back to point 1.  That’s one equilateral triangle.  We could make an equilateral triangle using points

{1, 6, 11}

{2, 7, 12}

{3, 8, 13}

(4, 9, 14)

{5, 10, 15}

After that, we would start to repeat.  There are five possible equilateral triangles, so 455 – 5 = 450 of these triangles are not equilateral.

Answer = (B)