GMAT Math: Factors

January 23, 2012

“How many odd factors does 210 have?”
“If n is the smallest integer such that 432 times n is the square of an integer, what is the value of y?”
“How many prime numbers are factors of 33150?”

If questions like these make you cringe, I’d like to convince you that only a few easy-to-understand concepts stand between you and doing these flawlessly.

Idea #1: Prime Numbers

This is probably review, but just for a refresher: a prime number is any positive integer that is divisible by only 1 and itself. In other words, a prime number has only two factors: itself and 1.

Numbers that have more than two factors are called composite.

By mathematical convention, 1 is the only positive integer considered neither prime nor composite.

The first few prime numbers are:

2 3 5 7 11 13 17 19 23 29

In preparation for the GMAT, it would be good to be familiar with this list. If you verify for yourself why each number from 2 to 30 is prime or composite, it will help you remember this list.

Occasionally, the GMAT will expect you know whether a larger two-digit number, like 67, is prime.

Of course, if the number is even, it’s not prime.

If a number ends in a digit of 5, it’s divisible by five.

For divisibility by 3, a good trick to know: if the sum of the digits is divisible by three, then the number is divisible by three. Here 6 + 7 = 13, not divisible by three, so 67 is not divisible by three.

To see whether a number less than 100 is prime, all we have to do is see whether it is divisible by one of the single digit prime numbers: 2, 3, 5, or 7.

We’ve already checked 2, 3, and 5. The number 67 is not divisible by 7: 7 goes evenly into 63 and 70, not 67. That’s enough checking to establish irrevocably that 67 is prime.

Idea #2: Prime Factorization

Every positive integer greater than 1 can be written in a unique way as a product of prime numbers; this is called its prime factorization. The prime factorization is analogous to the DNA of the number, the unique blueprint by which to construct the number. In other words, when you calculate the prime factorization of a number, you have some powerful information at your disposal.

How does one calculate the prime factorization of a number? In grade school, you may remember making “factor trees”: that’s the idea. To find the prime factorization of, for example, 48, we simply choose any two factors — say 6 and 8 — and then choose factors of those number, and then of those numbers, until we are left with nothing but primes.

Typically, once we are done, we sort the prime factors in numerical order:

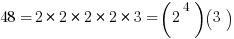
Once we have the prime factorization, what can we do with it? See the next two items.

Idea #3: The Number of Factors

Suppose the GMAT asks: how many factors does 1440 have? It would be quite tedious to count them all, but there’s a fast trick once you have the prime factorization. First of all, the prime factorization of 1440 is

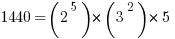
Each prime factor has an exponent (the exponent of 5 is 1).

To find the total number of factors:
a) Find the list of exponents in the prime factorization — here {5, 2, 1}
b) Add one to each number on the list — here {6, 3, 2}
c) Multiply those together —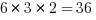

The number 1440 has thirty-six factors, including 1 and itself.
Suppose the GMAT asked the number of odd factors of 1440. We know that odd factors cannot contain any factor of 2 at all, so basically we repeat that procedure with all the factors except the factors of 2. Here: {2, 1} –> {3, 2} –> 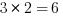3*2 = 6 . The number 1440 has 6 odd factors, including 1. Just for verification, the odd factors of 1440 are

{1, 3, 5, 9, 15, and 45}

This also means it has 36 – 6 = 30 even factors.

Idea #4: GCF and LCM

GCF = greatest common factor

LCM = least common multiple.

(Note: LCM and LCD are the same thing: a least common denominator, LCD, of two number is always their LCM.)

Suppose a GMAT Math question involves finding, say, the LCM (or LCD) of 30 and 48. There’s a very straightforward procedure to find the LCM.

Find the prime factorizations of the two numbers: 30 = 2*3*5 and 48 = 2*2*2*2*3
Find the factors they have in common – the product of these is the GCF. Here, the GCF = 2*3 = 6
Express each number as the GCF*(other stuff): 30 = 6*5 and 48 = 6*8
The LCM = GCF*(other stuff from first number)*(other stuff from the second number): LCM = 6*5*8 = 240

Let’s do one more, just for practice. Suppose, on a GMAT math problem, we need to find the LCM/LCD of 28 and 180

Step (a): 28 = 2*2*7, 180 = 2*2*3*3*5

Step (b): 28 = 2*2*7, 180 = 2*2*3*3*5; GCF = 2*2 = 4

Step (c) 28 = 4*7, 180 = 4*45

Step (d) LCM = 4*7*45 = 1260

Practice Questions:

1) The number of boxes in a warehouse can be divided evenly into 6 equal shipments by boat or 27 equal shipments by truck. What is the smallest number of boxes that could be in the warehouse?
(A) 27
(B) 33
(C) 54
(D) 81
(E) 162

2) How many odd factors does 210 have?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 8

3) If n is the smallest integer such that 432 times n is the square of an integer, what is the value of n?
(A) 2
(B) 3
(C) 6
(D) 12
(E) 24

4) How many distinct prime numbers are factors of 33150?
(A) Four
(B) Five
(C) Six
(D) Seven
(E) Eight

5) If n is a positive integer, then n(n + 1)(n – 1) is
(A) even only when n is even
(B) odd only when n is even
(C) odd only when n is odd
(D) always divisible by 3
(E) always one less than a prime number

Answers

1) C
2) E
3) B
4) B
5) D

Explanations

1) This tells us that the number of boxes is evenly divisible by both 6 and 27; in other words, it’s a common multiple of 6 and 27. The question says: what’s the smallest value it could have? In other words, what’s the LCM of 6 and 27? (This question is one example of a real-world set-up where the question is actually asking for the LCM.)

Step (a): 6 = 2*3 27 = 3*3*3

Step (b): 6 = 2*3 27 = 3*3*3 GCF = 3

Step (c): 6 = 3*2 27 = 3*9

Step (d) LCM = 3*2*9 = 54

Thus, 54 is the LCM of 6 and 27.

Answer: C.

2) Start with the prime factorization: 210 = 2*3*5*7

For odd factors, we put aside the factor of two, and look at the other prime factors.
set of exponents = {1, 1, 1}
plus 1 to each = {2, 2, 2}
product = 2*2*2 = 8
Therefore, there are 8 odd factors of 210. In case you are curious, they are {1, 3, 5, 7, 15, 21, 35, and 105}

Answer: E.

3) The prime factorization of a square has to have even powers of all its prime factors. If the original number has a factor, say of 7, then when it’s squared, the square will have a factor of 7^2. Another way to say that is: any positive integer all of whose prime factors have even powers must be a perfect square of some other integer. Look at the prime factorization of 432

432 = (2^4)*(3^3)

The factor of 2 already has an even power —- that’s all set. The factor of 3 currently has an odd power. If n = 3, then 432*n would have an even power of 2 and an even power of 3; therefore, it would be a perfect square. Thus, n = 3 is a choice that makes 432*n a perfect square.

Answer: B.

4) Start with the prime factorization:

33150 = 50*663 = (2*5*5)*3*221 = (2)*(3)*(5^2)*(13)*(17)

There are five distinct prime factors, {2, 3, 5, 13, and 17}

Answer: B.

5) Notice that (n – 1) and n and (n + 1) are three consecutive integers. This question is about the product of three consecutive integers.

If n is even, then this product will be (odd)*(even)*(odd) = even

If n is odd, this this product will be (even)*(odd)*(even) = even

No matter what, the product is even. Therefore, answers (A) & (B) & (C) are all out.

Let’s look at a couple examples, to get a feel for this

3*4*5 = 60
4*5*6 = 120
5*6*7 = 210
6*7*8 = 336
7*8*9 = 504

Notice that one of the three numbers always has to be a multiple of 3: when you take any three consecutive integers, one of them is always a multiple of 3. Therefore the product will always be divisible by 3.

Therefore, Answer: D.

BTW, for answer choice E of that question, you will notice that for some trios of positives integers, adding one to the product does result in a prime, but for others, it doesn’t.

3*4*5 + 1 = 61 = prime
4*5*6 + 1 = 121 = 11^2 (not prime)
5*6*7 + 1 = 211 = prime
6*7*8 + 1 = 337 = prime
7*8*9 + 1 = 505 = 5*101 (not prime)

This is a mathematical idea far far more advanced than anything on the GMAT, but it is mathematically impossible to create an easy rule or formula that will always result in prime numbers. The prime numbers follow an astonishingly complicated pattern, which is the subject of the single hardest unanswered question in modern mathematics: the Riemann Hypothesis. Fascinating stuff for leisure reading, but absolutely 100% not needed for the GMAT :).

Author

Mike MᶜGarry

Mike served as a GMAT Expert at Magoosh, helping create hundreds of lesson videos and practice questions to help guide GMAT students to success. He was also featured as “member of the month” for over two years at GMAT Club. Mike holds an A.B. in Physics (graduating magna cum laude) and an M.T.S. in Religions of the World, both from Harvard. Beyond standardized testing, Mike has over 20 years of both private and public high school teaching experience specializing in math and physics. In his free time, Mike likes smashing foosballs into orbit, and despite having no obvious cranial deficiency, he insists on rooting for the NY Mets. Learn more about the GMAT through Mike’s Youtube video explanations and resources like What is a Good GMAT Score? and the GMAT Diagnostic Test.

View all posts

Share7

Comments

64 responses to “GMAT Math: Factors”

Mike

January 12, 2020

Apologies for the incredibly elementary question here, but how does one just come up with these prime factor numbers? as an example, in your explanation of question 4 you state: “Start with the prime factorization: 33150 = 50*663”. How would you easily know that 33150 =50*663? Thank you.

Reply
1. Magoosh Test Prep Expert
  
  February 12, 2020
  
  Hi Mike,
  
  The best (and perhaps unsatisfying) answer is: practice! In this case in particular, the key is recognizing how to simplify the number to make it easier to work with. In this case, we start with 50 because we know that anything that ends in “50” or “00” will be divisible by 50. Once we do that, we can continue as we work with these slightly smaller numbers until we get to the prime numbers that can no longer be factored. If you struggle with these types of questions, our mental math flaschards might be helpful 🙂
  “
  
  Reply
Anna

May 30, 2019

Hi! I came across this GMAT practice problem, and was wondering if there is a trick for solving it more quickly? I solved it correctly and without a calculator, but it took me longer than the 2 min/question you want to average on the quant section of the GMAT, and I feel like there has to be a shortcut here.

[(1,527)^2 – (1,473)^2] / [(67)(54) + (54)(58)] = ?

Thank you so much!

Reply
1. Magoosh Test Prep Expert
  
  June 5, 2019
  
  Hm, good question! The fastest way is to notice that the numerator is a difference of squares, which you can convert to (1527+1473)(1527-1473). That’s (3000)(54). You can factor 54 out of the denominator and get 54(67+58). Then cancel the 54. Now you just have 3000/125, which equals 24. If that’s how you did it, then I’m afraid there doesn’t appear to be a faster way. Sometimes you just have to do some fast and careful arithmetic!
  
  Reply
Nihar

November 16, 2017

Hi, it’s true that a prime number has two positive factors, but why not two other negative factors? Say, it is claimed 3 has two factors, 1 and 3. But there are another two factors of 3 i.e. -1 and -3.

Reply
1. Magoosh Test Prep Expert
  
  November 17, 2017
  
  Hi Nihar,
  
  It’s true, the factors of 3 are actually -3, -1, 1, 3. If we specify positive and/or non-negative factors, then we only consider 1 and 3.
  
  Reply
Yacine

November 8, 2017

Hey guys, I don’t understand when you guys find the odd factors of 1440. You put 2,1 instead of 5,1.

Am I missing something?

Reply
1. Magoosh Test Prep Expert
  
  November 8, 2017
  
  Hi Yacine,
  
  We are disregarding the exponent of the prime factor of 2, so we are looking just at 5^2 and 3^1. That is where the 2 and 1 came from (the exponents of those prime factors). They are the odd factors, which is why we care about their exponents. 🙂
  
  Reply
Dave

November 7, 2017

Thanks for this.

Reply
Amy

October 28, 2016

Hi! I have a 7th grader that would like to know WHY it works to find the number of factors, to add 1 to each exponent, then multiply. This is Re: Idea 3. Thank you for any help!

Reply
1. Magoosh Test Prep Expert
  
  October 29, 2016
  
  Hi Amy,
  
  Happy to explain!
  
  When we add 1 to the number of the exponent, we are accounting for all cases of n^0 which help us to build the smaller factors we need to count. As we know, anything to the power of 0 is equivalent to 1, so when we calculate the combinations, this helps us account for factors that are made of some but not all of the prime factors (e.g. 3^0 * 5^1 = just 5) and also for the factor of 1 (when all prime factors have an exponent of 0).
  
  I hope that clarifies! 🙂
  
  Reply
Carmelite

April 18, 2016

What am I?

I am a square number that is less than 100. I am also a multiple of 4 and can be evenly divided by 3.

Reply
1. Magoosh Test Prep Expert
  
  April 18, 2016
  
  Hi Carmelite,
  
  The number fitting that description would be 36. 🙂
  
  Reply
Jenny

July 2, 2015

Hi Mike, this post was highly informative. Thanks! I just had a question about the first question. In your trick above for finding the LCM, you multiply the common factors to get the GCF. Although it is obvious that 3 is the GCF for 6 and 27, what happened to multiplying the common factors. If the common factors were multiplied, the GCF would have been 9. Is there an exception to this when the numbers have the same factors, in this case 3, where you don’t need to multiply? Thanks!

Reply
Karin

April 8, 2015

Hi Mike,

I have a question regarding the solution for the second question mentioned above. I understand the approach how we get to these 8 odd factors of the number 210, which is the main task of the question. However, looking at these 8 factors {1, 3, 5, 7, 15, 21, 35, and 105} I can’t properly follow why we have e.g. 35 as a factor of 210 but not 70 since 210 is divisible by 70 as well. May you explain me this situation?

Many thanks in advance,

Karin

Reply
1. Mike
  
  April 9, 2015
  
  Karin,
  I’m happy to respond! 🙂 My friend, remember that math is having an eye for details. That question did NOT ask the number of factors of 210. That question asked the number of ODD factors of 210. The eight factors listed there are all odd numbers. Certainly 70 and 2 and 10 and 210 are all factors of 210, but these are even numbers, and so don’t count in the list. Altogether, 210 has 16 factors, 8 odd and 8 even.
  Does all this make sense?
  Mike 🙂
  
  Reply
2. Vish
  
  May 12, 2016
  
  Hi Karin
  As author asked for only odd factors hence we cannot consider 70 as one of the factor whereas 35 is an odd factor.
  
  Reply
asu

January 5, 2015

Hi Mike,

To find the number of the odd factors you said you can’t have a factor of two. For example we have 2^3, 5^3, 6^4. To find the number of odd factors, do we just exclude 2 or 6 too? Since 2 is a factor of 6. If that’s the case we basically eliminate all the even numbers right? Thanks!

Reply
1. Mike
  
  January 6, 2015
  
  Dear Asu,
  What I said is that if you have a prime factorization, then you would eliminate only two, because two is the only even prime number. A factor of 6 would not appear in a prime factorization, because 6 is not a prime number.
  Does this make sense?
  Mike 🙂
  
  Reply
Tanya

November 24, 2014

Can you please give a definition of a distinct prime number? more specifically why is 1 not one of them?
Thank you!

Reply
1. Mike
  
  November 25, 2014
  
  Dear Tanya,
  I’m happy to respond! 🙂 The word “distinct” simply means “different.” For example, 12 = 2*2*3 — it has three prime factors but two of them are the same number, so it has just two distinct prime factors. Similarly, 900 = 2*2*3*3*5*5 has six prime factors in total, but many repeats among them: it has only three distinct prime factors. Does this make sense?
  As for why 1 is not prime number, see this post:
  https://magoosh.com/gmat/2012/gmat-math-one-is-not-a-prime-number/
  Mike 🙂
  
  Reply
Devyani

November 20, 2014

What will be the difference in the number of factors of N^2013 and N^2015 ?

Reply
1. Mike
  
  November 20, 2014
  
  Dear Devyani,
  Normally, we don’t answer outside questions in blog comments, but I’ll address this, because it’s quick. My friend, the question as you pose it is not well-defined. The number of factors would depend very much on N. If N is a prime number, then N^2015 has only two more factors — N^2014 and N^2015. By contrast, if N were a number loaded with factors, then the number of new factors in N^2015 would increase considerably. Even if N has just two prime factors (e.g. N = 6 or N = 15), the number of new factors would be in the 1000s. The question really doesn’t make sense without specifying N.
  Does all this make sense?
  Mike 🙂
  
  Reply
Rachael

August 15, 2014

Hello,

Thanks a lot for your very helpful explanations. This is pertaining to a question on the GMAT review number 13 on the diagnostic test. Although I have read the topic on remainder and tried the practice questions therein I still was unable to apply the format used to solve this particular question: if s and t are positive integers such that s/t = 64.12, which of the following could be the remainder when s is divided by t?

Please can you help me with this.

Regards,

Rachael

Reply
1. Mike
  
  August 15, 2014
  
  Dear Rachael,
  Normally, we do not answer outside questions on the blog, even official questions, but your question is so directly pertinent to this blog article that I decided to answer it here. 🙂
  Let R be the remainder. R/t = 0.12 = 12/100 = 3/25. So, it could be that R = 3 and t = 25, or they both could be multiples of those numbers. (3k)/(25k). R would absolutely have to be a multiple of 3. The only multiple of 3 is (E) 45.
  Does this make sense?
  Mike 🙂
  
  Reply
Karan

August 6, 2014

Hey Mike,

From Practice Question No. 5’s explanation, is it safe to assume that for a set of N consecutive integers, their product will ALWAYS be divisible by N?

Thanks! 🙂

Reply
1. Mike
  
  August 6, 2014
  
  Dear Karan,
  Yes, you are perfectly correct. Even if the set of N consecutive integers includes 0, the product will be zero, and zero is divisible by every integer. You are 100% correct.
  Mike 🙂
  
  Reply
Leszek

July 13, 2014

There’s a typo in Idea #3: The Number of Factors
the number should be 1440 and not 1400

Best

Reply
1. Mike
  
  July 13, 2014
  
  Dear Leszek,
  Thanks. I just fixed that! Best of luck to you, my friend.
  Mike 🙂
  
  Reply
Will

July 9, 2014

Hey Mike!

Thanks for the post! It’s really helpful!

I have an issue with Question #5.

If n=1, the result would be 1*2*0 = 0, which is not divisible by 3.

Then there would ne no correct answer.

Maybe shoud mention n is positive integer >1?

Am I wrong?

Thanks a lot!

William

Reply
1. Mike
  
  July 9, 2014
  
  Dear William,
  Zero is divisible by every positive integer, precisely because zero is a multiple of every positive integer.
  Mike 🙂
  
  Reply
sanjoy

June 8, 2014

Hi. My problem with LCM and GCF (word problems) is that I don’t know when to use each.how can I tell if they are asking me to calculate the LCM or the GCF? any language tricks????!!!! plz clarify.Thanks.

Reply
1. Mike
  
  June 9, 2014
  
  Dear Sanjoy,
  I’m happy to respond. 🙂 It’s true, these two ideas can show up in many different ways. I guess the only think I would say is: if the problem is collecting smaller groups to make a larger group, and asks what’s the smallest larger group that would do X — chances are good that’s a LCM problem. If we are adjusting the size of the smaller group, trying to make it as large as possible to make up some larger group, that’s a GCF. Does this make sense?
  Mike 🙂
  
  Reply
vivian

March 17, 2014

Hi,
I have a question regarding idea #3, I am having hard time understanding the concept here when you said that ” each prime factor has an exponent”. I am not seeing where these numbers coming from. can you help me out here? thanks,

Reply
1. Mike
  
  March 17, 2014
  
  Vivian,
  I’m happy to help. 🙂
  The number 432 is even, so let’s start by dividing it by 2.
  432/2 = 216
  Well, here, it would be helpful to have memorized that 6^3 = 216. I think it’s good to have memorized the perfect cubes of the first ten positive integers. But suppose you don’t have that memorized. Well, 216 is still even, so keep dividing by 2
  216/2 = 108
  108/2 = 54
  54/2 = 27
  That was four divisions by two, so the original number has four factors of two:
  432 = (2^4)*27
  Now, 27 is just 3^3 — that’s one you definitely have to have memorized! That gives us
  432 = (2^4)(3^3)
  All of those calculations you should be able to do without a calculator. Once we have it in this form, we can see the exponents, and see which ones are even or odd.
  Does all this make sense?
  Mike 🙂
  
  Reply
Misty

January 14, 2014

Mike – great blog post as always. Quick question – how come there is a good trick to finding the number of odd factors in an equation, but not even factors? In the example at the beginning of the post, there were 3×2=6 odd factors but not 6 even factors (5+1). Instead you had to find the total number of factors and subtract the number of odd factors to find even factors. Thank you!!

Reply
1. Mike
  
  January 14, 2014
  
  Misty,
  It’s easy to count all the factors. It’s also easy to count all the odd factors, because we simply exclude the 2’s and count everything else. For even factors, we would have to include 2 (or powers of 2) and count everything that includes it: it just a more complicated procedure, especially if there are several powers of two involves. The subtraction trick is easy to explain and works 100% of the time.
  Technically, if there are n powers of 2 in the prime factorization of the number, then 1/(n + 1) of the total factors will be odd, and n/(n + 1) of the total factors will be even. Now, would you rather remember that, or just the simple subtraction trick?
  Does all this make sense?
  Mike 🙂
  
  Reply
  1. Misty
    
    January 15, 2014
    
    Makes sense to me! I wouldn’t have realized it unless you pointed out the subtraction method at the beginning of the post, which I am glad you did. Perhaps it’s something worth highlighting in future posts/discussions on this topic. Thanks again Mike and keep up the great work!
    
    Reply
    1. Mike
      
      January 15, 2014
      
      Misty,
      You are quite welcome. Best of luck to you, my friend.
      Mike 🙂
      
      Reply
Kumar

January 9, 2014

Is problem 5, what if value of n is 1. Then the whole equation turns out to be zero. The answer option D does not seem to be correct in all situations.

Reply
1. Mike
  
  January 9, 2014
  
  Dear Kumar,
  This is a little appreciated mathematical fact, but zero is a multiple of every positive integer, and hence, zero is divisible by every positive integer. When we divide 0 by 3, we get a quotient of 0 with no remainder — if we can divide one number into another with no remainder, that’s the definition of divisibility. Does all this make sense?
  Mike 🙂
  
  Reply
Allan

July 22, 2013

Hello Mike. You state that 1 is not prime. You also state that all positive integers can be written as a product of prime numbers. You did not intend to include 1, in the latter statement, did you?

Reply
1. Mike
  
  July 23, 2013
  
  Allan,
  Good catch. That’s a niggling little exception that I forget to mention. I edited the text above to include this. The idea of prime factorizations and the Fundamental Theorem of Arithmetic apply to every positive integer *greater than 1*.
  Mike 🙂
  
  Reply
Allison

June 13, 2013

Hi Mike. Could you please explain how you arrived at the answer for #3 in further detail? I do not understand what you mean when you say that you “have to add additional factors for anything with odd exponents.”

Reply
1. Mike
  
  June 13, 2013
  
  Allison,
  I’m happy to explain this. 🙂
  As I say in the solution to #3 above, every prime factor in a perfect square must have an *even* exponent. If *any* of the prime factors has an odd exponents, then automatically the number cannot possibly be a perfect square. That’s the really BIG idea.
  Given that big idea, suppose we have a problem such as #3, — given some big number, say, N = 150, by what factor do we have to multiply this number, so that the product is a perfect square?
  Well, first we find the prime factorization of 150 –> (2^1)*(3^1)*(5^2). That has some odd exponents and some even exponents. The even exponents — they’re fine. The odd exponents are the problem — that’s precisely what prevents this number from being a perfect square right now. If we want to change this number, 150, into a perfect square, we have to multiply it by something that changes those odd exponents into even exponents. That’s precisely what I mean when I say that we “have to include additional factors for anything with odd exponents.” Here, the factor of 5, with an even exponent, is already all set. It’s those factors of 2 & 3, each with an odd exponent, that pose a problem and need reconjiggering. To turn this into a perfect square, we would have to bump each one of those exponents of 1 up to 2, the next biggest even number. This means, we need to multiply the original number, 150, by one factor of 2 and by one factor of 3, that is, by a factor of 6 altogether. Sure enough, if we multiply 150 by 6, we get 900, which is a perfect square, 30^2.
  Any number in which some of the exponents of prime factors are odd and some are even is thereby not a perfect square. If we want to multiply it by something to turn it into a perfect square, then for each factor with an odd exponent, we need to multiply once by that factor, to bump that exponent up from odd to even. In other words, we “have to include additional factors for anything with odd exponents.”
  Does all this make sense?
  Mike 🙂
  
  Reply
  1. Allison
    
    June 13, 2013
    
    Thanks so much Mike, that clears it up 🙂
    
    Reply
    1. Mike
      
      June 13, 2013
      
      Allison,
      You are quite welcome, my friend. Best of luck to you!
      Mike 🙂
      
      Reply
  2. Aniket
    
    June 26, 2015
    
    Gr8 explanation!!
    
    Reply
Nafiz

May 30, 2013

Hi Mike,

I wanted to ask a silly question. At question 4, when prime factoring 33,150, I got stuck when coming to 2 * 5 * 5 * 3 * 221.

221 can be factored into 13 * 17 which takes some work. Is there any quick way to go about these kind of numbers ???

Reply
1. Mike
  
  May 30, 2013
  
  Naifz,
  My friend, that is not at all a silly question. I will admit, I kinda cheated here — I picked a number for which I happen to know the factors, but which would probably be particularly difficult for most folks to factor on the fly without a calculator. In other words, I was being a little mean here — the GMAT will not be that mean to you.
  BTW, in case you’re curious, here’s a slick factoring trick, if you happen to notice it. If you happen to know that 15^2 = 225, and notice that 221 is exactly 4 less than 225 — of course, 4 = 2^2 — then we can express 221 as a Difference of Two Squares.
  a^2 – b^2 = (a + b)(a – b)
  221 = 225 – 4 = 15^2 – 2^2 = (15 + 2)(15 – 2) = 17*13
  I discuss these factoring techniques more in this post:
  https://magoosh.com/gmat/2012/advanced-non-calculator-factoring-on-the-gmat/
  Again, all this is at the very outer edge of what you might have to understand if you get absolutely everything else correct on the quant section and the CAT is throwing the hardest possible questions at you. Most folks will not have to worry about this at all.
  Does all this make sense?
  Mike 🙂
  
  Reply
  1. Nafiz
    
    May 30, 2013
    
    Hi Mike,
    
    Many thanx for your detailed explanation :). Do you think these kind of questions can come at GRE ? I was actually watching the magoosh video for counting divisors of large numbers, from there I came to your related post here.
    
    And what is the difference between GRE and GMAT quant questions qualitatively ? I have heard GMAT math is more hard, hence, do you think practicing GMAT type questions will improve my quant score at GRE ?
    
    Thanx again.
    
    Reply
    1. Mike
      
      May 31, 2013
      
      Dear Nafiz,
      This is a notch harder than anything the GRE is likely to throw at you, except perhaps in a very very hard challenge problem if one happens to be included in your Quant section.
      Yes, GMAT math is a tad harder than GRE math, and on the GMAT, you are not allowed to use a calculator, so it forces you to use all the mental math tricks and shortcuts which, if you master them, can save you a ton of time on the GRE. Many GRE students think the calculator to which they have access will help them on most problems, whereas actually, ETS designs many many problems to *punish* all who reflexively reach for the calculator rather than doing critical thinking first. Practicing GMAT math is a good way of avoiding all the “calculator traps.”
      Does all this make sense?
      Mike 🙂
      
      Reply
  2. Subh
    
    August 25, 2013
    
    I took more than 15 secs to realize that 221 is composite. But the derivation you provided using a^2-b^2 was wonderful. I’ll try to keep it in my mind next time I reach such a stage. Thanks
    
    Reply
    1. Mike
      
      August 25, 2013
      
      Dear Subh,
      I’m glad you found that helpful. Best of luck to you.
      Mike 🙂
      
      Reply
      1. D
        
        January 14, 2016
        
        Hi, Mike!
        
        #4 was confusing to me too, and your method of using the difference of squares was awesomely cool!
        
        So, quick follow-up question here for a situation where this method doesn’t work: in your post you mention that to check if a number is divisible by {2,3,5,7} for primes below 100. Is there a similar rule of thumb which I could use for numbers below 1000 etc.?
        
        Thanks a lot!
        
        Reply
        
        Magoosh Test Prep Expert
        
        February 1, 2016
        
        Hi D,
        
        Sorry about the late reply! The basic rule of thumb is that you only need to check for primes up to the square root of the number. So for numbers which are less than 100, you only need to check divisibility by prime numbers under √100 which is 10. This means that it is sufficient to check 2, 3, 5, and 7 to determine whether something is prime under 100.
        
        Over 100, you just need to figure out how far to check, really. If I need to check if 201 is prime, I should check up to the square root of 201 which is somewhere between 14 and 15, so I should check until 14. That means 2, 3, 5, 7, 11, and 13 are all possible divisors. For your question about 1000, I should check up to 32, so 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31. I hope that helps! 🙂
        
        Reply
test website

March 17, 2013

Hiya! I just would like to give a huge thumbs up for the great information you have right here on this post. I shall be coming again to your blog for more soon.

Reply
1. Mike
  
  March 17, 2013
  
  Thank you for your compliments.
  Mike 🙂
  
  Reply
taru

February 26, 2013

Hi Mike

In question #3, u checked straight away for 432×3 because it was odd or should we check with 2 first n then proceed?am i missing out something?because checking with 2 will kill time?is it a shortcut or something?

Taru

Reply
1. Mike
  
  February 26, 2013
  
  Dear Taru,
  What I checked first were the EXPONENTS of the factors. Anything with an even exponent could be ignored, and we had to add additional factors for anything with an odd exponents. That question is all about the exponents of the prime factors. It has nothing to do with whether the factors, 2 or 3, are odd. It has everything to do with whether the exponents of the prime factors are odd.
  Does that make sense?
  Mike 🙂
  
  Reply
jp27

October 24, 2012

If n is the smallest integer such that 432 times n is the square of an integer, what is the value of y?
(A) 2
(B) 3
(C) 6
(D) 12
(E) 24

I think there is a typo in this question, shouldn’t it read what is the value of N? (instead of Y)

Reply
1. Mike
  
  October 25, 2012
  
  Ooops! That’s a silly mistake I made there. I just corrected it. Thank you very much for the heads up.
  Mike 🙂
  
  Reply
Ravi Sankar Vemuri

April 28, 2012

“The prime factorization is analogous to the DNA of the number, the unique blueprint by which to construct the number” – Its a great analogy mike.
The examples on number of prime factors and odd factors are good.

Reply
1. Mike
  
  April 30, 2012
  
  Thank you. I’m glad you found it helpful. These are powerful strategies if you master them. Best of luck to you!
  Mike 🙂
  
  Reply