What is Logarithmic Differentiation? AP Calc Review

What is logarithmic differentiation? Basically, it’s a calculus tool that helps you to find derivatives of complicated functions involving a lot of multiplication, division, or powers. This review article walks you through the methods and provides plenty of example problems to help you succeed on the AP Calculus exams!

Properties of Logarithms

First of all, let’s review what a logarithm is. More specifically, we need to understand how the logarithm function can be used to break down complicated expressions.

You might want to check out the following article before getting started: AP Calculus Review: Properties of Exponents and Logartithms. However, the most important properties for us will be the product, quotient, and power properties for logarithms. Here, we focus on a particular logarithm: the natural logarithm, ln x, though the properties remain true in any base.

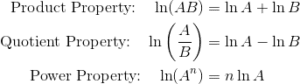
In other words, logarithms change…

1. products into sums,
2. quotients into differences, and
3. exponents into multiplication.

Using the Properties

I like to think of the logarithm as a powerful acid that can dissolve a complicated algebraic expression.

Let me illustrate the point with an example.

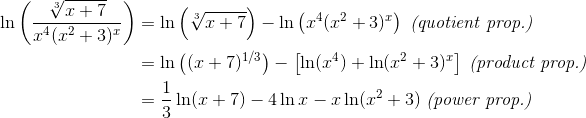
Notice how the original expression involves a huge fraction with roots and powers all over the place. After applying the properties of logarithms, the resulting expression mostly has only plus and minus. (Of course, there is a trade-off — there are now three natural logs in the simplified expression.)

Logarithmic Differentiation

Now let’s get down to business! How can we exploit these logarithmic simplification rules to help find derivatives?

The most straightforward case is when the function already has a logarithm involved.

Example 1

Find the derivative of .

Solution

First simplify using the properties of logarithms (see work above). Then you can take the derivative of each term. But be careful — the final term requires a Product Rule!

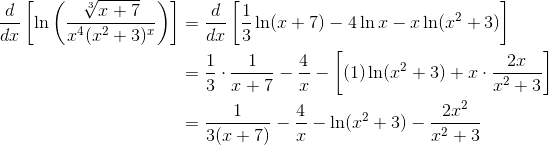
The General Method

In the above example, there was already a logarithm in the function. But what if we want to use logarithmic differentiation when our function has no logarithm?

Suppose f(x) is a function with a lot of products, quotients, and/or powers. Then you might use the method of logarithmic differentiation to find f ‘(x).

1. 1. First write y = f(x)
   2. Next, apply the (natural) logarithm function to both sides of the equation.
   3. Then use the product, quotient, and/or power properties to break down the expression on the right. In other words, simplify ln(f(x)) algebraically.
   4. Now apply the derivative operator to both sides.
   5. Use your rules of differentiation to find the derivatives. Note that the left-hand side requires implicit differentiation. (Check out: AP Calculus Review: Implicit Variation for details.)
      
   6. Solve for dy/dx by multiplying both sides by y. In your answer, don’t forget to replace y by f(x).

Example 2

Use logarithmic differentiation to find the derivative of:  

Solution

Let’s follow the steps outlined above. The first two steps are routine.

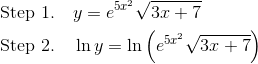
On the other hand, Step 3 requires us to break down the logarithmic expression using the properties. The work in this step depends on the function. In our case, there is a product of two factors, so we’ll start with the product property. The power property helps to break down the radical. Finally, don’t forget the cancellation rule: ln(e^x) = x.

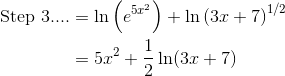
Next, in Steps 4 and 5 apply the derivative and work out the right-hand side.

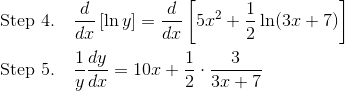
Finally, in Step 6, we solve for the unknown derivative by multiplying both sides by y. Don’t forget to substitute back the original function f(x) in place of y.

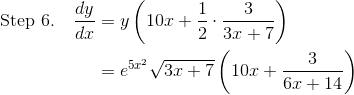
Functions Raised to a Function Power

A very famous question in Calculus class is: What is the derivative of x^x ?

• The answer is NOT x x^{x – 1}, because the Power Rule for Derivatives cannot be used when the power includes a variable.
• The answer is NOT x^x ln x, because the Exponential Rule for Derivatives cannot be used when the base includes a variable.

So what is the derivative of x^x ?

Well, it turns out that only logarithmic differentiation can decide this one for us!

In fact any time there is a function raised to a function power (that is, neither the exponent nor the base is constant), then you will have to use logarithms to break it down before you can take a derivative.

Let’s see how it works in the simplest case: x^x.

First, write y = x^x.

Then, apply the logarithm to both sides:   ln y = ln x^x.

Break down the right-hand side of the equation using the algebraic properties of logarithms. In this case, only the power property plays a role.

ln y = x ln x

Now you can take derivatives of the functions on both sides. But be careful… the function on the right requires a Product Rule.

(1/y)(dy/dx) = (1) ln x + x(1/x) = ln x + 1

Finally, multiply both sides by the original function (y = x^x) to isolate dy/dx.

dy/dx = x^x(ln x + 1)

And there you have it! The derivative of x^x turns out to be trickier than you might have thought at first, but it’s not impossible.

Summary

• Logarithmic differentiation is a method for finding derivatives of complicated functions involving products, quotients, and/or powers.
• You can use the algebraic properties of logarithms to break down functions into simpler pieces before taking the derivative.