AP Calculus Review: Implicit Variation

Implicit variation (or implicit differentiation) is a powerful technique for finding derivatives of certain equations. In this review article, we’ll see how to use the method of implicit variation on AP Calculus problems.

What is Implicit Variation?

The usual differentiation rules, such as power rule, chain rule, and the others, apply only to functions of the form y = f(x). In other words, you have to start with a function f that is written only in terms of the variable x.

But what if you want to know the slope at a point on a circle whose equation is x² + y² = 16, for example?

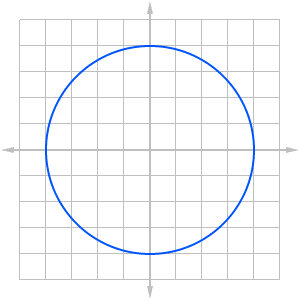
Here, it would be possible to solve the equation for y and then proceed to take a derivative. However, that’s not really the best way!

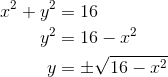
For one thing, that square root will make finding the derivative more challenging.

For another, you really have two separate functions — one using the plus (+), and the other using minus (-) in front of the radical! Which one should you use for finding the derivative? Well, that depends on whether you want the top or bottom semicircle.

An Easier Way

It would be so much simpler to just work with the original equation (x² + y² = 16 in this discussion) rather than to solve it out for y.

Well we’re in luck! The method of implicit variation does exactly that!

The Method of Implicit Variation (Differentiation)

Given: an equation involving both x and y.

Goal: To find an expression for the derivative, dy/dx.

Method:

1. Apply the derivative operation to both sides. This means that you should write d/dx before both sides of your equation. This is like an instruction to indicate that you’ll be doing derivatives in the next step.
2. When taking derivatives, treat expressions of x alone as usual. However, if there are any expressions of y, then you must treat y as an unknown function of x. In particular, follow these additional rules:

   

   Basically, whenever you take a derivative of a term involving y, then you must tack on dy/dx.

3. Solve (algebraically) for the unknown derivative, dy/dx. At this point, every problem may be different, but there are a few common themes that I’ve found over the years that seem to apply fairly often.
   1. Group terms that have a factor of dy/dx on the left side of the equation. Those terms without the derivative should end up on the right side.
   2. Factor out by the common dy/dx.
   3. Divide by the expression in front of dy/dx

Keep in mind, your final answer may involve both x and y.

Where Do those dy/dx Factors Come From?

This is something that had bugged me for a long time after first learning the method myself. Why do we have to tack on an “extra” dy/dx when taking derivatives involving y?

The big idea here is that y is actually a function. We just have no idea what that function is!

In a typical (or explicit) function, such as y = x³ – 3x + 2, y has already been isolated. In this example, we know that the function is f(x) = x³ – 3x + 2.

However, an implicit equation has not been solved for y. In fact, it may be impossible to do so!

So we do the next best thing, which is simply to use our rules of calculus, including the Chain Rule, whenever we encounter the unknown function y in our equation.

That’s where the extra dy/dx comes from. There is a hidden Chain Rule lurking in the background!

Example — Free Response

Consider the equation x² – 2xy + 4y² = 52.

(a) Write an expression for the slope of the curve at any point (x, y).

(b) Find the equations of the tangent lines to the curve at the point x = 2.

(c) Find at (0, √(13)).

(a) Slope and the Derivative

The keyword slope indicates that we must find a derivative. It would be way too difficult to solve the equation explicitly for y. So this is a job for implicit differentiation!

First, apply d/dx to both sides.

The next few steps are just working out the derivatives. Perhaps the trickiest part is the term involving 2xy. Think of that as the product of 2x with an unknown function y = f(x). That way, it may make more sense why we must use the Product Rule for that term.

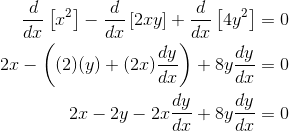
Finally, solve for the unknown derivative algebraically. Don’t forget to group, factor and divide!

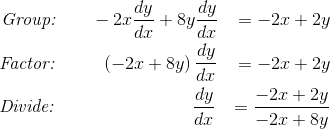
We can factor out a common factor of 2 on top and bottom to get a final answer:

(b) Finding the Tangent Lines

There’s a clue in the word lines. You should expect there to be more than one answer.

First find the y-coordinate(s) that correspond to x = 2. We do this by plugging x = 2 into the original equation.

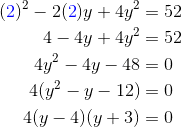
So there are two solutions: y = 4 and y = -3. This means that there are two different points at which we must find a tangent line. At each point, plug in the (x, y) pair into dy/dx from part (a) to find the slope.

Point 1: (2, 4). Slope = .

Therefore, using point-slope form for the line, we get y = (1/7)(x – 2) + 4.

Point 2: (2, -3). Slope = .

Again using point-slope form, we find y = (5/14)(x – 2) – 3.

(c) Implicit Second Derivatives

To find the second derivative of an implicit function, you must take a derivative of the first derivative (of course!).

However, all of the same peculiar rules about expressions of y still apply.

Note that we are using the Quotient Rule to start things off.

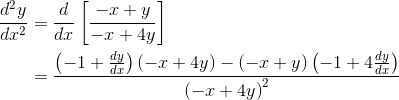
Now, the good news is that we don’t have to simplify the expression any further. This is because they are looking for a numerical final answer. So we just have to plug in the given (x, y) coordinates.

But what about the two spots where “dy/dx” shows up?

Well we already have an expression for dy/dx from part (a). Simply plug in your (x, y) coordinates to find dy/dx…

…and now you can plug that into the second derivative expression as well.

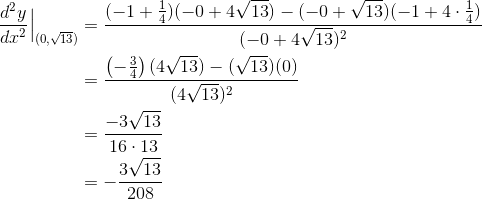
Summary

On the AP Calculus AB or BC exam, you will need to know the following.

• How to find the derivative of an implicitly-defined function using the Method of implicit variation (a.k.a. implicit differentiation).
• What the derivative means in terms of slope and how to find tangent lines to a curve defined implicitly.
• How to compute second derivatives of implicitly-defined functions.