
Reading a derivative graph is an important part of the AP Calculus curriculum. Typical calculus problems involve being given function or a graph of a function, and finding information about inflection points, slope, concavity, or existence of a derivative.
Does the derivative exist?
Firstly, looking at a graph we should be able to know whether or not a derivative of the function exists at all. Our derivative blog post has a bit more information on this.
The three situations where a derivative does not exist
There is no derivative if there is a discontinuity on the curve.
This is any time that there is a break in a curve, where two parts of the curve do not connect.
Types of discontinuity:
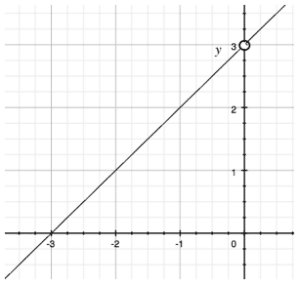
There is a removable discontinuity. Imagine a linear function such as y = x + 3. If we were to add in a restriction where x is not defined at x = 0, we would have such a discontinuity.
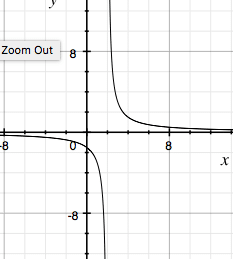
There is an infinite discontinuity. This occurs when we have any equation where there is a break between two continuous sections of a curve due to asymptotes reaching infinity. For example, let y = 3/(x-2). Notice, we have two vertical asymptotes that do not connect.
Lastly, we have a jump discontinuity. This happens with piecewise functions where two sections simply do not connect.
A derivative does not exist where there is a sharp corner.
![]()
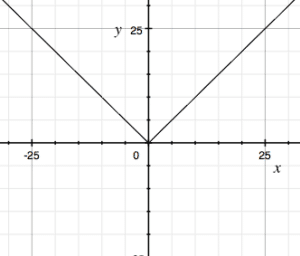
This often occurs with absolute value problems. Let us look at the graph of y = √x2
At x = 0, there is no derivative because we have a sharp bend in the curve.
Lastly, there is no derivative anywhere there is a vertical section of graph.
If there is a vertical section of a graph, the slope is undefined; therefore, the derivative does not exist.
Reading the Derivative Graph.
Looking at a graph, we should be able to quickly eye the slope at any and get a rough idea of what the slope should be. This makes it easy to match up a graph with its derivative.
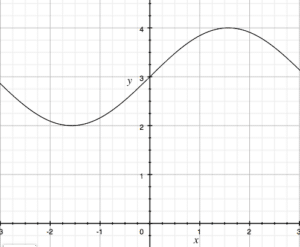
Looking at the first graph, can you figure out which of the three below is the graph of the derivative?
f'(x):
a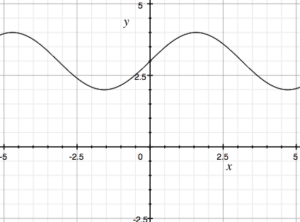
b
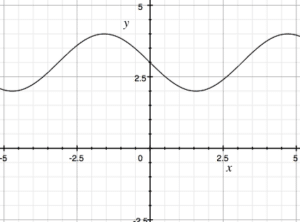
c
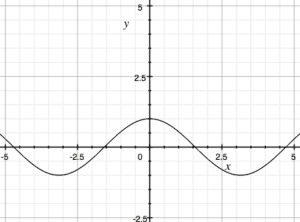
Few keys to getting the correct answer. We should immediately see that this is some sort of trigonometric function. We know the slope of the function is 0 at a handful of points; therefore the graph of the derivative should go through the x-axis at some point. As well, looking at the graph, we should see that this happens somewhere between -2.5 and 0, as well as between 0 and 2.5. This alone is enough to see that the last graph is the correct answer.
Graphing a function based on the derivative and the double derivative.
The derivative and the double derivative tells us a few key things about a graph:
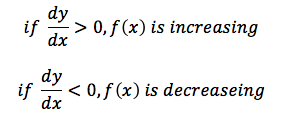
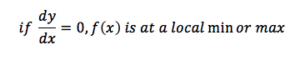
(Good AP Practice: How can we tell whether it’s min or max?)
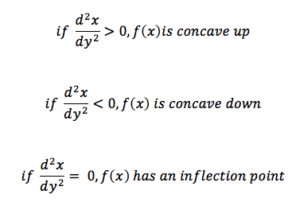
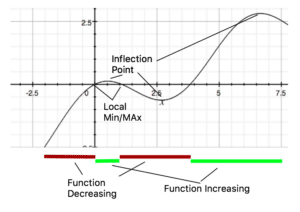
The following is a graph of the derivative of f(x).
Here is the graph of the function. Can we see how they correspond?
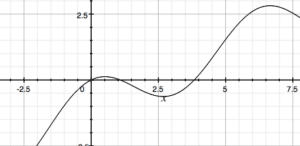
Being able to read graphs of a derivative and knowing what the general shape of the original function should be is an important part of the AP Calculus curriculum. Make sure you know how to determine inflection points, local minimums and maximums, and where a function is increasing or decreasing.

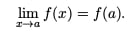



Leave a Reply