AP Calculus Review: Discontinuities

What’s a discontinuity? Any point at which a function fails to be continuous is called a discontinuity. In fact, there are various types of discontinuities, which we hope to explain in this review article.

Points of Discontinuity

The definition of discontinuity is very simple. A function is discontinuous at a point x = a if the function is not continuous at a.

So let’s begin by reviewing the definition of continuous.

A function f is continuous at a point x = a if the following limit equation is true.

Think of this equation as a set of three conditions.

1. The limit must exist. That is, for some finite number L.
2. The function value must exist. In other words, f(a) exists.
3. The limit must agree with the function value. So, the number L that you get by taking the limit should be the same value as f(a).

When one or more of these conditions fails, then the function has a discontinuity at x = a, by definition.

The first condition, that the limit must exist, is especially interesting. A limit may fail to exist for a variety of reasons. If the limit as x → a does not exist, then we can say that the function has a non-removable discontinuity at x = a. Then, depending on how the limit failed to exist, we classify the point further as a jump, infinite, or infinite oscillation discontinuity.

Jump Discontinuities

One way in which a limit may fail to exist at a point x = a is if the left hand limit does not match the right hand limit.

In the graph shown below, there seems to be a “mismatch.” As x approaches 1 from the left, that part of the graph seems to land on y = -1. On the other hand, as x approaches 1 from the right, the values of y seem to get closer and closer to y = 3.

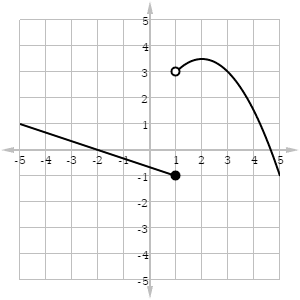
In limit notation, we would write:

Because the left and right limits do not agree, the limit of f(x) as x → 1 does not exist.

Therefore, by definition, the function f is discontinuous at x = 1. This kind of discontinuity is known as a jump (for obvious reasons).

Infinite Discontinuities (Vertical Asymptotes)

In some functions, the values of the function approach ∞ or -∞ as x approaches some finite number a. In this case, we say that the function has an infinite discontinuity or vertical asymptote at x = a.

You might think of an infinite discontinuity as an extreme case of jump discontinuity.

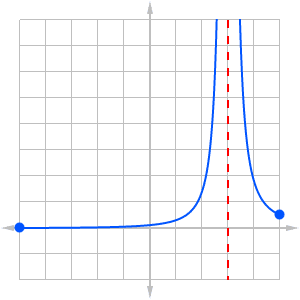
Typically, you’ll find this behavior anywhere there is a division of the form nonzero over zero.

For instance 3x/(x + 12) has an infinite discontinuity at x = -12, because that is where the denominator becomes 0 while the numerator is nonzero (3 × -12 = -36).

Example

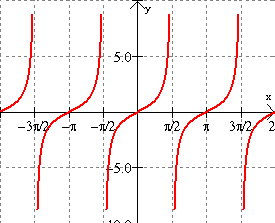
Locate and classify the discontinuities of f(x) = tan x on the interval [-2π, 2π].

Solution

Note that tan x = (sin x)/(cos x), and the denominator, cos x, is equal to zero at all points of the form π/2 + nπ. There are four x-values within the interval [-2π, 2π] that qualify: x = -3π/2, -π/2, π/2 and 3π/2. Plugging each one into the numerator, sin x, we verify that the top is nonzero when the bottom is zero. Thus, f has an infinite discontinuity at four points: x = -3π/2, -π/2, π/2 and 3π/2 within the interval [-2π, 2π]

The graph can help us to visualize what’s going on near those point.

Infinite Oscillation Discontinuities

Most of the functions that you meet are fairly boring and predictable. Even at a jump or infinite discontinuity, you can say something about how the values of the function behave. However if your function has an infinite oscillation discontinuity at a point x = a, then things get wild!

Consider the graph of f(x) = sin(1/x).

Approaching the origin, the curve goes up and down more and more often. In fact as x → 0, from either the left or right, we can see how the oscillations get completely out of hand! It’s almost as if the curve wants to make sure it hits every point in the range between -1 and 1 at x = 0.

No matter how far we zoom in on the graph, it just gets wilder and wilder.

The reason for this strange behavior has to do with the fact that sin x itself is periodic. Then replacing x by 1/x in the argument has the effect of taking all those infinitely many periodic waves of the sine function as x → ∞ and squeezing them next to the origin instead.

At any rate, since there is no single value of y to which the curve seems to be heading as x → 0, the limit does not exist at x = 0.

Therefore, f(x) = sin(1/x) has a discontinuity at x = 0, of the infinite oscillation variety.

Removable Discontinuities

The last category of discontinuity is different from the rest. In the previous cases, the limit did not exist. In other words, condition 1 of the definition of continuity failed. Next we’ll discuss what happens if condition 1 holds (the limit exists), but either condition 2 or 3 fail.

A function f has a removable discontinuity at x = a if the limit of f(x) as x → a exists, but either f(a) does not exist, or the value of f(a) is not equal to the limiting value.

If the limit exists, but f(a) does not, then we might visualize the graph of f as having a “hole” at x = a. You might imagine what happens if you filled in that hole. If it really is a removable discontinuity, then filling in the hole results in a continuous graph!

Let’s take a look at the graph below.

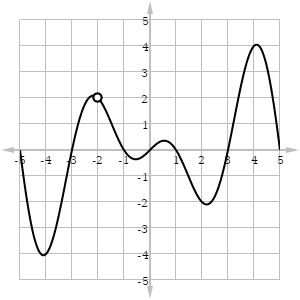
There is a hole at x = -2. In fact, the graph would be continuous at that point if the hole at (-2, 2) were filled in. That’s the clue that we’re dealing with a removable discontinuity at x = -2.

There is one more case to consider. Suppose both conditions 1 and 2 hold for a function at a given point, but condition 3 fails. That is, the limit exists, the function value exists, but they are different values.

This situation happens in the graph shown below.

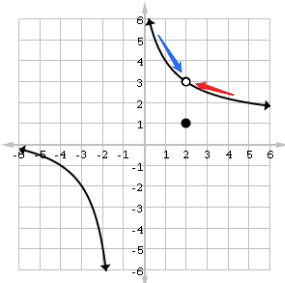
Focus at what happens near x = 2.

There is a well-defined limit value. Because the curve approaches y = 3 from the left and the right, the limit is equal to 3.

But f(2) = 1 (based on the location of the dot). Since the value of f is not the same as the limiting value here, we can say that f has a removable discontinuity at x = 2.

Example

Identify where the function has a removable discontinuity and determine the value of the function that would make it continuous at that point.

Solution

Look to the denominator. We know that f will be undefined whenever the bottom of the fraction is equal to 0. That happens when 2x – 4 = 0, or after solving for x, we find x = 2.

So we already know there is some kind of discontinuity at x = 2 (because f(2) does not exist — see condition 2 of the definition of continuity). But is it removable? That takes finding a limit.

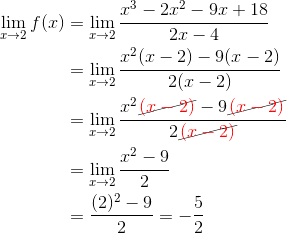
Because the limit value exists, we now know for sure that there is a removable discontinuity at x = 2.

Moreover, the limit itself tells us what the value should be to make f continuous: -5/2.