The absolute extrema of a function are the largest and smallest values of the function. What is the most profit that a company can make? What is the least amount of fence needed to enclose a garden? Once you know how to find the absolute extrema of a function, then you can answer these kinds of questions and many more!
Overview: What are Absolute Extrema?
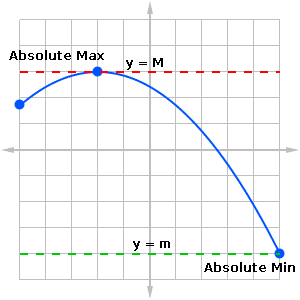
The absolute extrema of a function f on a given domain set D are the absolute maximum and absolute minimum values of f(x) as x ranges throughout D.
In other words, we say that M is the absolute maximum if M = f(c) for some c in D, and f(x) ≤ M for all other x in D.
We define the absolute minimum m in much the same way, except that f(x) ≥ m for all x in D.
Functions with Discontinuity
Sometimes a function may fail to have an absolute minimum or maximum on a given domain set. This often happens when the function has a discontinuity.
Domain Sets and Extrema
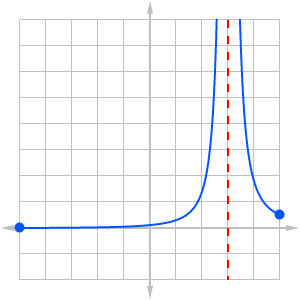
Even if the function is continuous on the domain set D, there may be no extrema if D is not closed or bounded.
For example, the parabola function, f(x) = x2 has no absolute maximum on the domain set (-∞, ∞). This is because the values of x2 keep getting larger and larger without bound as x → ∞. By the way, this function does have an absolute minimum value on the interval: 0.
However, there may still be issues even on a bounded domain set. The function below has neither absolute minimum nor maximum because the endpoints of the interval are not in its domain. Note, the open circles on the graph mean that those points are missing, so there cannot be any extrema at those points.
The Extreme Value Theorem
In practice, we usually require D to be a closed interval of the form [a, b] for some constants a < b. In that case, the Extreme Value Theorem guarantees both absolute extrema must exist.
- The Extreme Value Theorem (EVT) If a function f is continuous on a closed, bounded interval [a, b], then f attains both absolute extrema on that interval.
Just be careful: the EVT only works in one direction. If the function is continuous on a closed, bounded interval, then it must have absolute extrema on that interval. However a function may fail to meet the conditions of the EVT and still have an absolute maximum and/or minimum.
Finding the Absolute Extrema
In the case that f is continuous on [a, b], then the following procedure will locate the absolute extrema.
The Closed Interval Method
The method requires computing a derivative. If you need a refresher, check out this Calculus Review: Derivative Rules.
- Find all critical numbers of f within the interval [a, b]. That is, set f '(x) = 0, solve for x, and only consider those solutions x that satisfy a ≤ x ≤ b.
- Plug in each critical number from step 1 into the function f(x).
- Plug in the endpoints, a and b, into the function f(x).
- The largest value is the absolute maximum, and the smallest value is the absolute minimum.
Example
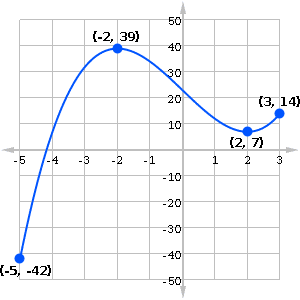
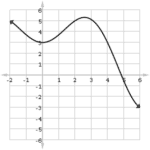
Let’s find the absolute extrema of f(x) = x3 – 12x + 23 on the interval [-5, 3].
Because f is continuous on [-5, 3], which is a closed and bounded interval, the EVT guarantees both an absolute maximum and minimum must exist on the given interval. Furthermore, we can using the Closed Interval Method to find them.
Step 1: First find the critical numbers.
f '(x) = 3x2 – 12 = 3(x2 – 4) = 3(x – 2)(x + 2)
Setting 3(x – 2)(x + 2) = 0, we find two critical numbers: -2 and 2, both of which are in the given interval.
Steps 2 and 3: I tend to combine these steps in my work. Build a table of x-values on the left, including the critical numbers and the endpoints of the interval. Then in the right column, plug each one into f(x).
| x | f(x) = x3 – 12x + 23 | |
|---|---|---|
| -5 | -42 | Min |
| -2 | 39 | Max |
| 2 | 7 | |
| 3 | 14 |
The absolute maximum value is 39 (at x = -2), and the absolute minimum is -42 (at x = -5).
Looking at the graph of f, you can verify the max and min values.
Summary
- The absolute extrema of a function on a given domain set D are the greatest and least values of the function on D.
- The Extreme Value Theorem guarantees that a continuous function must have absolute extrema on a bounded, closed interval.
- You can use the Closed Interval Method to locate the absolute extrema.
Now that you know more about absolute extrema, you can maximize your score on the AP Calculus exams!




Leave a Reply