Parametric functions only show up on the AP Calculus BC exam. In this article we’ll take a close look at these kinds of functions which turn out to be extremely useful in the sciences.
In fact, this is one case in which the phrase “It’s not rocket science!” isn’t really appropriate. Parametric equations play a huge role in rocket guidance systems!

What are Parametric Functions?
While they may at first seem foreign and confusing, parametric functions are just a more flexible way to track motion in the plane.
Usually you might think of a function as y = f(x). The graph of a function must pass the Vertical Line Test (VLT), and as a result, your options are limited.
Sure you can use typical functions to define parabolas, catenaries and even sinusoidal waves, but what about a the orbit of a planet?
Certainly any circular or elliptical graph fails the VLT. So you can’t write a function of the form y = f(x) for this situation.
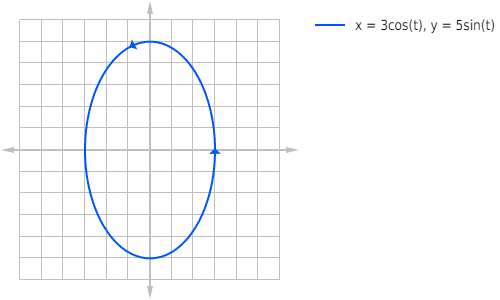
Instead, you need to be able to specify both x and y in terms of some independent parameter, t. That’s where the term parametric comes from.
Definition
A parametric function (or a set of parametric equations) is a pair of two functions specifying the x– and y-coordinates of a point moving through the plane.
![]()
Think of each function as a separate control, one for x and one for y. Perhaps the best physical example of parametric equations is the Etch-A-Sketch.
The Etch-A-Sketch has two knobs, one controlling the vertical, and one controlling the horizontal position of a stylus. When the two knobs work together, almost anything can be drawn!
Graphing
There is a straightforward way to graph any parametric function.
- Choose a number of sample t-values. If there is a given range of values, a ≤ t ≤ b, then you must stick to values within that interval. Otherwise, just pick a wide range of values, both positive and negative.
- For each sample t, plug it into x = f(t) and into y = g(t) to find out the corresponding x– and y-coordinates.
- Plot each (x, y) pair on the plane. Then connect the dots in the order of increasing t.
Example Graph
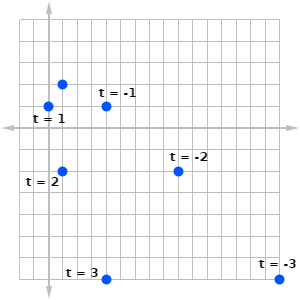
Graph the parametric function defined by x = t2 – 2t + 1 and y = –t2 + 2.
Because there was no range specified for t, let’s just pick a few easy numbers to work with. Remember, use both positive and negative values to get a good sense for how the function behaves.
I like to organize my work in a table.
| t | x = t2 – 2t + 1 | y = –t2 + 2 | (x, y) |
|---|---|---|---|
| -3 | 16 | -7 | (16, -7) |
| -2 | 9 | -2 | (9, -2) |
| -1 | 4 | 1 | (4, 1) |
| 0 | 1 | 2 | (1, 2) |
| 1 | 0 | 1 | (0, 1) |
| 2 | 1 | -2 | (1, -2) |
| 3 | 4 | -7 | (4, -7) |
Next, plot these points on a coordinate plane.
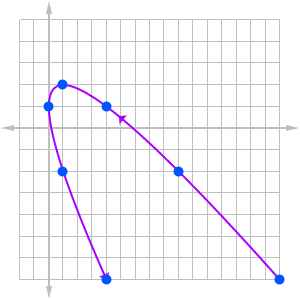
Finally, connect the dots in order of increasing t.
Derivatives of Parametric Functions
Now that you have seen some graphing, let’s talk about slope. As you know, the derivative measures slope. But how do you find the derivative of a set parametric equations?
We must be careful, because there are two equations to deal with. Should you take the derivative of f(t) or g(t)?
In fact, you’ll have to take the derivative of both. Here is the formula for dy/dx.
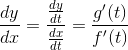
Example — Tangent Line
What is the equation of the tangent line at t = π/6 for the parametric function x = 3 cos t, y = 3 sin t?
Using the derivative formula, we get:
dy/dx = (3 cos t)/(-3 sin t) = -cos t / sin t.
Plugging in t = π/6, the slope is -cos(π/6)/sin(π/6) = -1.732.
Now we also need to know what the x– and y-coordinates are for the point in question.
x = 3 cos(π/6) = 2.598, and y = 3 sin(π/6) = 1.5.
Therefore, using the point-slope form, the equation of the tangent line is:
y = -1.732(x – 2.598) + 1.5
Derivatives and Velocity
There is another interpretation of the derivative that allows you to compute the velocity of an object traveling along a parametric curve.
The idea is to think of a parametric function as a vector.
Thinking of t as time, then both the velocity vector and accelerations vectors are simply derivatives in each component.
![]()
For more information about vector functions, check out this AP Calculus BC Review: Vector-Valued Functions
Example — Velocity
Find the velocity vector at t = 1 for an object traveling according to the parametric function x = t2 – 2t + 1, y = –t2 + 2.
First find the derivative of each component function.
v(t) = (2t – 2, -2t).
Therefore at time t = 1, the velocity vector is:
v(1) = (0, -2).
Length Integrals
Another important formula to memorize is the arc-length integral. If you want to know the length of the curve traced out by the parametric function x = f(t), y = g(t), for a ≤ t ≤ b, then just set up and compute the following integral.
![]()
Example — Length of a Parametric Curve
Find the length of the curve defined by x = 3 cos t, y = 3 sin t on the interval [0, π/2].
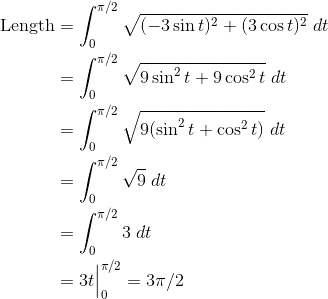
Summary
Parametric functions show up on the AP Calculus BC exam. You should know the following.
- How to graph or interpret the graph of a parametric function
- Finding the slope at any given point on a parametric curve
- Computing the velocity vector
- Finding the length of the curve



Leave a Reply