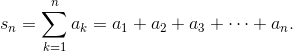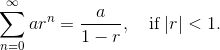With the AP Calculus BC exam right around the corner, now’s the time to gear up your preparations. Hopefully you’ve started studying already. And if not, then what are you waiting for? Either way, I hope this Calculus BC cram sheet could be just the right way for you to review for the test.
About the Test
The AP Calculus BC exam is a standardized test lasting 3 hours and 15 minutes. If you’re planning to take the BC test, then you have to put in a lot of time studying and prepping.
A high score (4-5) may qualify you for college credit or equivalency for two full semesters of calculus.
Format of the Exam
- There are two main sections, multiple choice and free response. You might find the following articles helpful as you prepare for each type of problem.
- Can I use a Calculator on the AP Calculus Exam? Well yes, but only on the parts of each section that all calculators. For the no calculator sections, check out these AP Calculus No Calculator Section Tips.
- If you can’t come up with the right answer, then guessing doesn’t hurt your score. But try to eliminate answers that you are sure can’t be correct.
- Pace yourself in the multiple choice section. If you find yourself spending too much time on a question, skip it and move on.
- Use a two-pass method. On your first pass through the problems, answer what you can. Then take a second pass, if time permits.
- On your second pass, make sure that your bubble sheet accurately records what you think the answers are. Also, spend some time on more challenging questions that you couldn’t crack the first time around.
- In the free response section, spend enough time to clearly write out each step. Most of your points will be earned by showing and carrying out proper methods for each problem. Explain, communicate, and justify.
- After answering each question, re-read the question statement to ensure that you’ve understood what they were asking.

General Tips
Click here to learn more about the format of the exam: What is the Format of the AP Calculus BC Test?.
What’s on the Exam?
There are four Big Ideas that comprise the material on the test.
- Limits and Continuity
- Derivatives and Their Applications
- Integrals and Their Applications
- Sequences and Series
Check out What Topics are on the AP Calculus BC Exam?.
Basically, the AP Calculus BC exam covers everything that the AB exam covers, and then some. So it may be helpful to review this AP Calculus AB Cram Sheet first.
In what follows, we will highlight a few of the definitions, properties, theorems, and formulas you’ll need for the test, focusing on those items that are specific to Calculus BC.
AP Calculus BC Cram Sheet
The best way to study for any AP exam is to review over a period of many weeks or months. Unfortunately, you probably won’t do well if your study plan consists of an all-night
cram session on the night before the test.

So don’t think of this Calculus BC cram sheet as a substitute for weeks and weeks of hard work. Instead, think of it as a concise summary to help you review.
Big Idea 1. Limits and Continuity
The AB and BC tests both cover the same topics as far as limits and continuity.
So because this Calculus BC cram sheet is focusing on just the BC material, let’s move on to the other Big Ideas.
Big Idea 2. Derivatives and Their Applications
Here again, the AB and BC tests cover a lot of the same ground. However, the BC test does go beyond the AB in the inclusion of vector-valued, parametric, and polar functions and their derivatives as well as Euler’s method for estimating solutions to differential equations.
Vector-Valued and Parametric Functions
On the AP Calculus BC test, vector and parametric functions are essential the same thing. They are both defined by a single input variable (or parameter) t, and multiple outputs, x and y.
A vector function looks like this: F(t) = (f(t), g(t)).
A parametric function looks like a list of two functions: x = f(t) and y = g(t). Another term for this is a set of parametric equations.
In either case, the values of the function are pairs (x, y) defined by plugging in t-values to f(t) and g(t).
For example, the parametric equations defining a circle of radius 4 centered at the origin are x = 4cos t and y = 4sin t, for 0 ≤ t ≤ 2π.
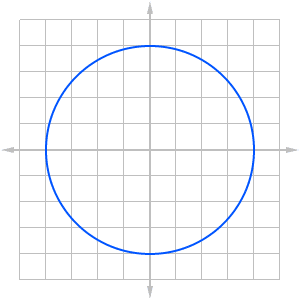
Vector and parametric functions are both examples of multivariable functions. Check out this AP Calculus Review: Multivariables for more information.
You should know how to find the first and second derivatives and what their interpretations are.
![]()
Recall, the speed of a particle is found by taking the length, or magnitude, of the velocity.
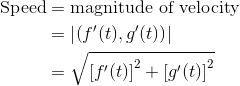
The slope of a parametric curve is given by:
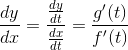
Polar Functions
A polar function r = f(θ) defines a curve by how far away from the origin (r) each point is at any given angle (θ).
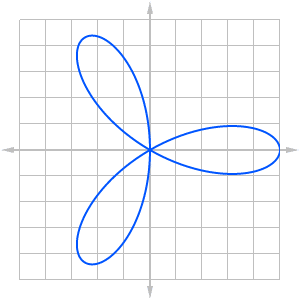
There are conversion formulas that may help to transform an equation written in terms of x and y (Cartesian coordinates) into a polar equation, and vice versa.
![]()
If you need to know the slope of a polar curve r = f(θ), then use the following polar derivative formula.
![]()
Euler’s Method
Suppose you have an initial value problem of the following form.
![]()
Then, with any chosen small step size h, you may approximate the solution using the following procedure algorithm:
![]()
Big Idea 3. Integrals and Their Applications
On the AP Calculus BC exam, you will be expected to know additional techniques of integration, including integration by parts and partial fractions. Here’s a summary of all of the antidifferentiation techniques you’ll need for the test: AP Calculus Exam Review: Antidifferentiation
You’ll also need to understand improper integrals.
Certain applications of integration not typically found on the AB exam will also show up, including:
- Particle moving along a vector-valued or parametric curve.
- Arc length for polar and parametric functions
- Area bounded by polar curves
- Logistic growth
Particle Motion
If a vector function v(t) represents the velocity of a particle, then its indefinite integral provides the position function.
The total distance covered by a particle whose vector function is (x(t), y(t)) is exactly the same as the arc length, which we’ll talk about next.
Arc Length Integrals
Arc length measures the distance along the curve between two specified points.
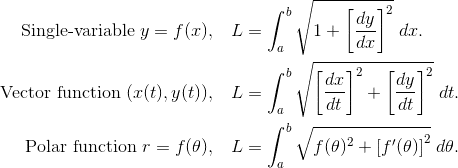
Note that the formula for the arc length of a parametric function is exactly the same as the formula for the vector function.
Area in Polar Coordinates
To find the area enclosed by a polar function r = f(θ) between two specified angles, use the following formula.
![]()
Logistic Growth Model
The logistic growth model is defined by a certain differential equation,
![]()
Here, k and a are supposed to be constants. You can find a nice description of the logistics equation as well as information about how to work with it here.
Big Idea 4. Sequences and Series
Last but not least, the AP Calculus BC exam includes topics on sequences and series. In this Calculus BC cram sheet, I’ll provide just a few concepts and formulas that you should be aware of.
Sequence and Series Concepts
- A sequence is just a list of numbers, (a1, a2, a3, …).
- A series is the sum of a sequence, which typically involves infinitely many terms.
- The nth partial sum of a series is the sum of the first n terms:

- A series converges if and only if the sequence of its partial sums converges.
- There are many different tests for convergence of series. Most of these tests only work on specific kinds of series.
- p-series test (convergent if p > 1)
- Geometric series test (convergent if |r| < 1)
- Comparison test and limit comparison
- Integral test
- Root and ratio tests
- Alternating series test
- The sum of a geometric series formula:

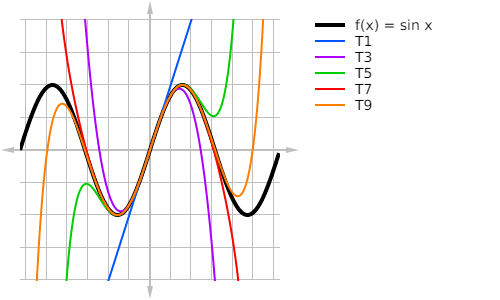
Taylor and Maclaurin Series
A function may be represented by a Taylor series centered at x = c.
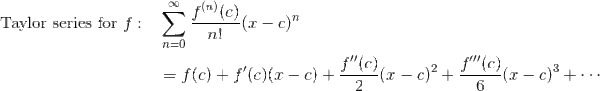
A Maclaurin series is simply a Taylor series centered at x = 0.
It’s very useful to have memorized the Maclaurin series for some common functions.
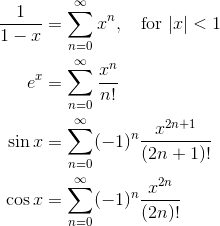
Power Series and Convergence
The Taylor and Maclaurin series are examples of power series.
Make sure you know how to find the radius and interval of convergence for a given power series. Often, the easiest method to use is the root or ratio test.
The Lagrange error bound is useful for quantifying how accurately a Taylor polynomial approximates the function. Check out this video for more details.
Final Thoughts
Keep in mind, this Calculus BC cram sheet should only serve as a review checklist for you, not as a primary studying resource.
If you are reading this with plenty of time to spare before the exam, then consider setting up a 3-Month AP Calculus Exam Study Guide. Or, if you’ve been putting things off, maybe this 1-Month AP Calculus Exam Study Guide is more up your alley.