There are 45 problems in the AP Calculus BC Exam multiple choice section. Let’s take a look at the kinds of questions you might see on the test. Below, you can find some information about the format of the test and then a sampling of practice problems with solutions provided at the end.

Format of the Exam
The Calculus AB and Calculus BC exams both have the same format.
- Section I — Multiple Choice (1 hour and 45 minutes total)
- Part A — 30 questions — 60 minutes — No calculator.
- Part B — 15 questions — 45 minutes — Graphing calculator required.
- Section II — Free Response (1 hour and 30 minutes total)
- Part A — 2 questions — 30 minutes — Graphing calculator required.
- Part B — 4 questions — 60 minutes — No calculator.
AP Calculus BC Exam Multiple Choice Practice
Go find a nice quiet distraction-free location to work on these problems. In fact, you should treat this practice set like the real deal. Even though there are not 45 questions in this practice, there are enough to get the idea of what could show up on the exam.
The suggested time limits are scaled down appropriately. First see what you can get through in the time allotted. Then after time runs out, you can always go back and complete the rest.
Remember, on the AP calculus BC exam multiple choice section, you don’t have to show your work. Furthermore, there is no penalty for a wrong choice. So if you have no idea how to do a problem, try to eliminate a choice or two and then guess among the remaining answers.
Part A
(Time — 20 minutes — 10 questions)
(A calculator may not be used on this part of the examination)
- The position of a particle at time y ≥ 0, in seconds, is given by x = t3 – 12t2 + 45t – 1 and y =t3 – 15t2 + 63t + 5. At what values of t is the particle at rest?(A) t = 3, 5
(B) t = 3
(C) t = 3, 5, 7
(D) t = 5, 7
- What is the value of
 ?(A) 2/9
?(A) 2/9
(B) 2/3
(C) 3
(D) Diverges
 (A) π/4
(A) π/4
(B) π/3
(C) π/2
(D) Diverges
- The length of a curve from x = 1 to x = 5 is given by
 . If the curve contains the point (1, 10), which of the following could be the curve?(A) y = 64x2 – 54
. If the curve contains the point (1, 10), which of the following could be the curve?(A) y = 64x2 – 54
(B) y = 64x2 + 1
(C) y = 8x2 + 2
(D) y = 4x2 + 6
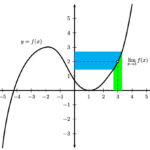
- The graph of the function f is shown below.

If
 , what is
, what is  ?
?(A) 5
(B) 8
(C) 12
(D) 16
- Find the area inside one loop of the curve r = 3cos 2θ.(A) π/4
(B) 3π/8
(C) 9π/8
(D) π
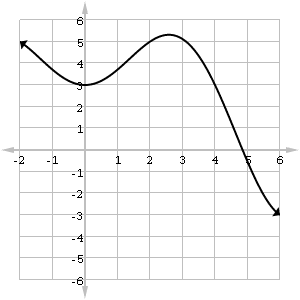
- For what values of x does the series
 converge?(A) -1/4 < x < 1/4
converge?(A) -1/4 < x < 1/4
(B) -4 < x < 4
(C) -1 < x < 1
(D) All real numbers
 =(A)
=(A) 
(B)

(C)

(D)

- Which of the following series converges?

(A) II only
(B) III only
(C) II and III
(D) I and III
- What is the coefficient of x6 in the Taylor series for
 about x = 0?(A) 1/720
about x = 0?(A) 1/720
(B) 1/24
(C) 1/3
(D) 1/6
Part B
(Time — 15 minutes — 5 questions)
(A graphing calculator is required for some questions on this part of the examination)
 (A) 4ln|2x + 1| – 3ln|x – 1| + C
(A) 4ln|2x + 1| – 3ln|x – 1| + C
(B) 8ln|2x + 1| – 3ln|x – 1| + C
(C) 8ln|2x + 1| + 3ln|x – 1| + C
(D) 4ln|2x + 1| + 3ln|x – 1| + C
- The monthly costs that a certain company incurs can be modeled by
 , where t is measured in months. What is the total cost incurred by the company in months 12 ≤ t ≤ 24, to the nearest dollar?(A) $32,105
, where t is measured in months. What is the total cost incurred by the company in months 12 ≤ t ≤ 24, to the nearest dollar?(A) $32,105
(B) $34,820
(C) $35,271
(D) $36,529
- Use Euler’s Method with h = 0.25 to estimate y(1) if y ‘ = 3y – 1 and y(0) = 1.(A) 5.873
(B) 6.013
(C) 6.586
(D) 7.312
- A particle moves along the x-axis so that its acceleration at any time t ≥ 0 is given by a(t) = 12sin 2t – 8cos 2t m/s2. If its initial velocity is 12 m/s and its initial position is x = 8, what is its position, in meters, at time t = 2 seconds?(A) 42.96
(B) 51.09
(C) 102.17
(D) 115.22
- Let R be the region in the first quadrant between the graphs of y =
 , y = sin x, and the y-axis. The volume of the solid that results when R is revolved about the x-axis is(A) -0.565
, y = sin x, and the y-axis. The volume of the solid that results when R is revolved about the x-axis is(A) -0.565
(B) 0.565
(C) 0.395
(D) -0.395
Solutions
Answer Key:
| 1. B | 6. C | 11. D |
| 2. A | 7. B | 12. B |
| 3. B | 8. A | 13. C |
| 4. D | 9. C | 14. A |
| 5. C | 10. D | 15. B |
Short explanations are given below for each AP calculus BC exam multiple choice problem.
Problem 1
(B) t = 3
First, find the derivative of each component. Then set them both equal to zero and solve.
![]()
The only t-value that makes both components equal to 0 is t = 3.
Problem 2
(A) 2/9
Re-express the sum as a geometric series. Then, because the common ratio has absolute value less than 1, the series converges and you may use the sum of a geometric series formula.
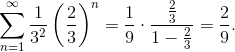
Problem 3
(B) π/3
Use the antiderivative formula involving arctan. And don’t forget about the infinite limit.
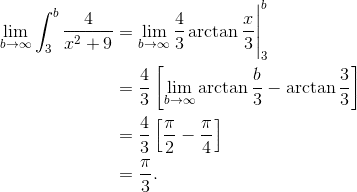
Problem 4
(D) y = 4x2 + 6
Comparing the arc-length formula to the given integral, it must be the case that [f ‘(x)]2 = 64x2. This implies that f ‘(x) = ±8x. Therefore, f(x) = ±4x2 + C.
However none of the answer choices have a negative coefficient on the square term, so we know that f(x) = 4x2 + C. Finally, using the given information that f(1) = 10, solve for C and put together the final answer:
f(x) = 4x2 + 6.
Problem 5
(C) 12
Using the Fundamental Theorem of Calculus (the part that deals with the derivative of an accumulation function),
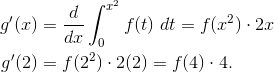
According to the graph, f(4) = 3, so the final answer is 3(4) = 12.
Problem 6
(C) 9π/8
A quick sketch of the graph indicates that the region is between -π/4 and π/4.
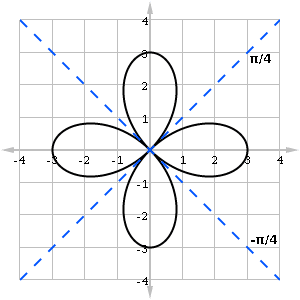
Using the integral formula for area of a polar region,
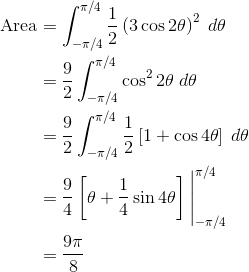
Problem 7
(B) -4 < x < 4
Use the Ratio Test.
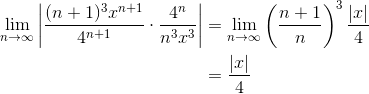
So the series will converge if |x|/4 < 1, or |x| < 4. Since the series diverges at both x = 4 and x = -4, the interval of convergence is -4 < x < 4.
Problem 8
(A) ![]()
Integration by parts.
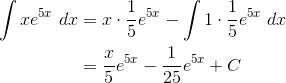
Problem 9
(C) II and III
Series I is a p-series with p = 3/4. Since 3/4 < 1, this series diverges. Series II is also a p-series, but with p = 4/3 > 1. Thus, series II converges. Series III is alternating and since 1/√n → 0 as n → ∞, series III converges.
Problem 10
(D) 1/6
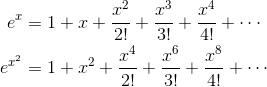
The coefficient of x6 is 1/(3!) = 1/6.
Problem 11
(D) 4ln|2x + 1| + 3ln|x – 1| + C
This integral requires the method of partial fractions. Omitting the algebraic steps that determine the numerator values, we have
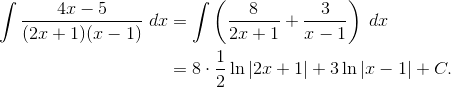
Problem 12
(B) $34,820
We can use a definite integral to find the total cost over a period of time. However, the integral would be too difficult to work out by hand, so use your calculator’s numerical integration function.
![]()
Problem 13
(C) 6.586
The table below records the steps of Euler’s Method.
| n | xn | yn | yn' |
|---|---|---|---|
| 0 | 0 | 1 | 3(1) – 1 = 2 |
| 1 | 0.25 | 1 + 0.25(2) = 1.5 | 3(1.5) – 1 = 3.5 |
| 2 | 0.5 | 1.5 + 0.25(3.5) = 2.375 | 3(2.375) – 1 = 6.125 |
| 3 | 0.75 | 2.375 + 0.25(6.125) = 3.906 | 3(3.906) – 1 = 10.718 |
| 4 | 1 | 3.906 + 0.25(10.718) = 6.586 |
Problem 14
(A) 42.96
Integrate acceleration twice to find the position function. After each integration, use the initial data to solve for the constant of integration.
![]()
Since the given initial velocity is 12, we find C = 18.
![]()
Now the initial position x0 = 8 implies that C = 6. Thus, the position function is:
x(t) = -3 sin 2t + 2 cos 2t + 18t + 6.
Plugging in t = 2, using a calculator, we find x(2) = 42.96 seconds.
Problem 15
(B) 0.565
A graph of the two curves helps to locate the bounds of integration.
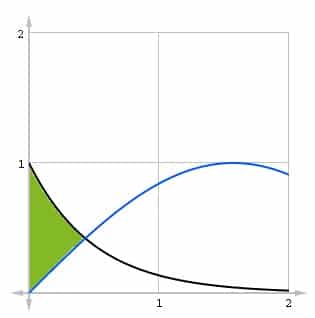
The left bound is 0, but the right bound is the x-coordinate of the point of intersection of the two curves. You your calculator to numerically approximate this point, which is roughly 0.4336.
Then set up the volume integral using the washer method. Finally, find the volume using the numerical integration function on your calculator.
![]()
What’s Next?
Now that you’ve gotten some practice with multiple choice questions, check out these AP Calculus BC Exam Free Response Practice Problems. Practice makes perfect!

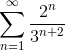 ?(A) 2/9
?(A) 2/9
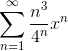 converge?(A) -1/4 < x < 1/4
converge?(A) -1/4 < x < 1/4
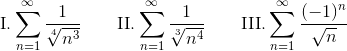



Leave a Reply