In this article, we’ll be talking about that dreaded A-word, asymptote. In my experience, students often get hung up on the term and may believe these kinds of problems are impossible. But with a solid understanding of the concepts, and a few algebraic techniques in your toolbox, it is not too difficult to locate the vertical asymptotes of a function.
The Types of Asymptotes
There are three types of asymptote: horiztonal, vertical, and oblique. This article focuses on the vertical asymptotes. Horiztonal asymptotes are discussed elsewhere, and oblique asymptotes are rare to see on the AP Exam (For more information about oblique, or slant asymptotes, see this article and this helpful video).
Vertical Asymptotes
A vertical asymptote (or VA for short) for a function is a vertical line x = k showing where a function f(x) becomes unbounded. In other words, the y values of the function get arbitrarily large in the positive sense (y→ ∞) or negative sense (y→ -∞) as x approaches k, either from the left or from the right.
A vertical asymptote is like a “brick wall” that the function cannot cross. Imagine that you are flying in an airplane and up ahead you see a huge mountain. If you can’t go left or right around the mountain what would you do? You’d probably fly upward to avoid hitting it. Now imagine that mountain is vertical and infinitely high. Then you might fly upwards forever to avoid hitting it, and still never get over the mountain!
A function may have any number of vertical asymptotes, or none at all. Some functions even have infinitely many VAs. The graph shown below has vertical asymptotes at x = -3 and x = 1.

Because the definition involves variables approaching fixed values, it should come as no shock that limits must be involved somehow. The precise definition for a vertical asymptote goes as follows. We say that x = k is a VA for a function f(x) if either the left-hand or right-hand limit to x = k is infinite:
![]()
Finding Vertical Asymptotes
There are two main ways to find vertical asymptotes for problems on the AP Calculus AB exam, graphically (from the graph itself) and analytically (from the equation for a function). We’ll talk about both.
Determining Vertical Asymptotes from the Graph
If a graph is given, then look for any breaks in the graph. If it appears that a branch of the function turns toward the vertical, then you’re probably looking at a VA. It helps to sketch a vertical line at the x-value where you think the asymptote should be (see the graph shown above). Note, if part of the graph actually touches your vertical line, then that line is not an asymptote after all.
Determining Vertical Asymptotes from the Equation
If you need to find vertical asymptotes on the AP Exam, you will most likely not be given the graph. So you’ll need to know what to look for in the equation of the function itself. Ask yourself, where does this function have an infinite limit? We’ll see how this applies to two different kinds of functions, rational functions and trigonometric functions.
Vertical Asymptotes in Rational Functions
If your function is rational, that is, if f(x) has the form of a fraction, f(x) = p(x) / q(x), in which both p(x) and q(x) are polynomials, then we follow these two steps:
1. Factor both the numerator (top) and denominator (bottom). This is very important because if any factors end up canceling, then they would not contribute any vertical asymptotes.
2. Once your rational function is completely reduced, look at the factors in the denominator. If there is a factor involving (x – a), then x = a is a VA. If there is a factor involving (x + a), then x = –a is a VA. Note how the sign seems to be opposite both times (just like solving a factored polynomial that has been set equal to zero).
Practice Finding Vertical Asymptotes
Let’s see how our method works. Find the vertical asymptote(s) of each function.
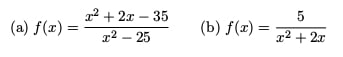
Solutions:
(a) First factor and cancel.
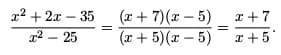
Since the factor x – 5 canceled, it does not contribute to the final answer. Only x + 5 is left on the bottom, which means that there is a single VA at x = -5.
(b) This time there are no cancellations after factoring.
![]()
We find two vertical asymptotes, x = 0 and x = -2.
Vertical Asymptotes for Trigonometric Functions
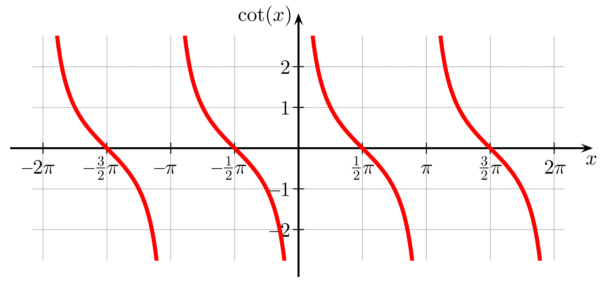
The method of factoring only applies to rational functions. However, many other types of functions have vertical asymptotes. Perhaps the most important examples are the trigonometric functions. Out of the six standard trig functions, four of them have vertical asymptotes: tan x, cot x, sec x, and csc x. In fact, each of these four functions have infinitely many of them!
For example, f(x) = cot x has a VA at every integer multiple of π. In other words, x = n π is a VA for every n = 0, ±1, ±2, ±3, …
Using your Graphing Calculator
More general functions may be harder to crack. If you are working on a section of the exam that allows a graphing calculator, then you may simply graph the function and try to spot the breaks in the graph at which the y-values become unbounded. Some calculators, like the TI-84, even have an option called detect asymptotes, which will automatically graph the VAs. Just be careful, though; if your viewing window is too small, then you may miss a VA.
Conclusion
Asymptotes are just certain lines that tell us about the behavior of functions. A vertical asymptote shows where the function has an infinite limit (unbounded y-values). It is important to be able to spot the VAs on a given graph as well as to find them analytically from the equation of the function. Your graphing calculator can also help out. With a little time and practice, these techniques can easily be mastered, and so vertical asymptotes don’t have to be the “brick wall” that stops you from going far on the AP Calculus exam!

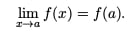


Leave a Reply