First, a couple questions to start:
1) A large research project was scheduled over the course of a 28-month period, and a budget of $84,000 was allotted for the course of the entire project. After seven months, the project had spent $19,800. Was the project at this point over budget or under budget, and by how much?
-
(A) under, $4200
(B) under, $1200
(C) under, $700
(D) over $1800
(E) over $5800
2) A special municipal payroll tax charges not tax on a payroll less than $200,000 and only 0.1% on a company’s payroll above $200,000. If Belfried Industries paid $200 in this special municipal payroll tax, then they must have had a payroll of
-
(A) $180,000
(B) $202,000
(C) $220,000
(D) $400,000
(E) $2,200,000
Solutions will come at the end of this article.
Multiple perspectives in math
Sometimes GMAT students, especially folks who are not very confident in math, think about GMAT math problems in a very binary framework — they get the problem either right or wrong. If they get the problem right, they assume they know “the way” to do the problem, and if they get the problem wrong, they read the solutions to determine what “the way” was.
This, it turns out, is a quite naïve approach to math. Many times, especially on GMAT problems, there is not a single “right way” to do the problem, but a variety of approaches. Sometimes one, a non-standard approach, is more efficient than the standard “approved by your Algebra Two teacher” approach. Sometimes two or more solutions are equally efficient, or perhaps one more than the other depending on the proclivities of the test taker.
Folks who want to improve their GMAT Quant performance often over-emphasize the importance of practice a sheer quantity of problems and often vastly underestimate the profound importance of learning to see multiple solutions to a single problem. These students often underestimate the importance of studying carefully the solution to a problem they got right: it may be that the solution shows a considerably more efficient approach than they devised, and studying and learning this new method of solution may well save them crucial time in the future.
It is very much a poverty mentality in math for the student to be caught in a view of “can I do anything that might lead to a solution?” I understand some folks might feel this initially, especially if they are returning to math after a long absence. Recognize, though, that somewhere between the beginner stage and master, one had to learn to adjust one’s perspective from that question to “of all the possible approaches, what would be the best, the most efficient, for this problem?” Mathematical mastery is about thinking in terms of options among possible solutions, and more quickly one can adopt this sort of perspective, the faster one will move toward mastery.
Some options
The foregoing discussion, well raising an important point, was somewhat abstract. What are some examples of some alternative approaches, beyond the way that your Algebra Two teacher told you that you were supposed to solve the problem? Here are some thoughts.
a. thinking in terms of ratios & proportions often simplifies problems, and scale factors are a powerful proportional reasoning trick to know and understand
b. sometimes a visual solution is very helpful, engaging the skills of the right brain; this can be especially important if algebraic information about x & y can be moved into the x-y plan
c. instead of following equations in a very lock-step, left-brain way, one can reason directly with the data, especially with percents — well if 5% is this, that must me 10% is that, and therefore 30% would be three times that. Arguably, this is a variant of proportional reasoning, specific to percents.
d. Remember that backsolving is an important option when all five answers are numbers.
e. Remember that, especially if the answers are spread widely, estimation might be a valid solution, and much faster than a direct & detailed calculation.
Those are some examples, but nothing replaces the value of reading carefully the solution to each and every math problem you solve — most especially the solutions of problems you get right. It may be that, say, for 80% of the problems you get right, you did exactly what was in the solution, and that’s fine, but for that other 20%, what you could learn about mathematical reasoning in those solutions could activate the next level of mathematical potential for you.
Summary
In the solution section below, I will show a few different alternates for solving each version of the problem. Here’s another question from inside Magoosh for practice:
3) http://gmat.magoosh.com/questions/829
If you have anything you would like to share after reading this, please let us know in the comments section below.
Practice problems: multiple solutions
1) METHOD ONE: The straightforward methodical Algebra Two approach (not terribly efficient)
First, figure out the cost of each month.
Now, multiply by seven months: 7*($3000) = $21,000. That would be the budgeted amount, the amount theoretically supplied to the project. The real amount spent is less than this, so it is under budget.
$21,000 – #19,800 = $1200
Answer = (B)
METHOD TWO: a slightly more efficient approach using ratios.
Notice that seven months is exactly 1/4 of 28-months. Therefore, after seven months, they should have spent 1/4 of the total budget.
Again, this budgeted amount is more than what was spent, so what was spent was under budget.
$21,000 – #19,800 = $1200
Answer = (B)
2) METHOD ONE: the step-by-step algebraic inefficiency method:
payroll tax = 0.1% of (payroll income – 200,000)
Remember that 0.1% as a decimal is 0.001.
payroll tax = 0.001*(payroll income – 200,000)
200 = 0.001*(x – 200,000)
200/0.001 = 200,000 = x – 200,000
200,000 + 200,000 = 400,000 = x
Answer = (D)
NB: this method requires one to know a couple tricky ideas about percents & decimals.
METHOD TWO: thinking about percents.
Well, 0.1% of something is $200. Multiply this by ten — then 1% of something is $2000. Now, multiply this by 100 —- 100% of something is $200,000. That’s the amount over the $200,000 baseline, so the total payroll must have been the sum, $400,000. Answer = (D)
METHOD THREE: backsolving
One would use this either if one didn’t know how to do either of the first two approaches, or simply if one thought this would be faster.
Start with (C).
Suppose payroll = $220,000. The first $200,000 is tax free, so only $20,000 is taxed at 0.1%. Well, 1% of $20,000 — knock off two zeros: 1% would be $200. Divide by ten now: 0.1% would be $20. That’s too little. Payroll must be more, so we can immediately eliminate choice (A) & (B) & (C). Even if we had no more time to work on this problem, we could employ solution behavior very effectively at this point.
You could try another answer, (D) or (E), or you could just notice — with (C), the taxable part was ten times too small, because the payroll tax was ten times too small. We need a taxable portion that is ten times bigger — instead of $20,000, we need a taxable portion of $200,000. Add this to the baseline = $400,000. Answer = (D).


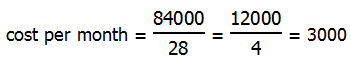
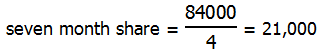




Leave a Reply