Here are four reasonably challenging problems about sets.
1) At a certain school of 200 students, the students can study French, Spanish, both or neither. Just as many study both as study neither. One quarter of those who study Spanish also study French. The total number who study French is 10 fewer than those who study Spanish only. How many students study French only?
-
(A) 30
(B) 50
(C) 70
(D) 90
(E) 120
2) In a company of 300 employees, 120 are females or non-binary. A total of 200 employees have advanced degrees, and the rest have a college degree only. If 80 employees are males with college degree only, how many are females or non-binary folks with advanced degrees?
-
(A) 60
(B) 80
(C) 100
(D) 120
(E) 160
3) In a certain school, there are 80 Freshmen, 100 Sophomores, and 220 Upperclassmen, drawn from three cities: A, B, and C. Sixty percent of students are from A, 30% from B, the rest from C, and all these students from C are freshmen. Half the student from B are upperclassman, and the rest are split evenly between the other two grades. How many sophomores are from A?
-
(A) 60
(B) 70
(C) 80
(D) 90
(E) 100
4) There are a total of 400 students at a school, which offers a chorus, baseball, and Italian. This year, 120 students are in the chorus, 40 students in both chorus & Italian, 45 students in both chorus & baseball, and 15 students do all three activities. If 220 students are in either Italian or baseball, then how many student are in none of the three activities?
-
(A) 40
(B) 60
(C) 70
(D) 100
(E) 130
Solutions will be given at the end of the article.
Set problems
For two or more overlapping categories, in scenarios in which any given member can belong to all, some, or none of the categories, Venn Diagrams can be helpful. If there are two separate variables, and each member is classified according to each variable, then the Double Matrix Method can be helpful. If reading the articles at either of those links gives you insights on any of these problems, you may want to give the problems a second look before reading the solutions below.
Practice problem solutions
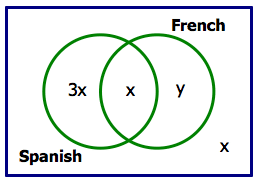
1) Let x be the number of folks studying both, which means it is also the number of folks studying neither.
“One quarter of those who study Spanish also study French.” If the Spanish students studying French are x, then all Spanish students are 4x, and those who do not study French are 3x. Also, let y be the number of students who study French but not Spanish.
“The total number who study French is 10 fewer than those who study Spanish only.” In other words,
x + y = 3x – 10
10 = 2x – y
Also, notice that the total number of students is 200:
3x + x + y + x = 200
5x + y = 200
We have two equations with two unknowns. Add the equations (2x – y = 10) and (5x + y = 200), and we get
7x = 210
x = 30
y = 50
And the number who study French is x + y = 80. Answer = (B)
2) This problem is handled best with a double-matrix solution.
Because there are 120 females or non-binary folks, we know the rest are males. Because there are 200 with advanced degrees, we know there are 100 with college degrees only.
At this point, we could go either way: we could figure out all the numbers in the “college” row or all the numbers in the “male” column.
Either way, it is easy to fill in the last box:
Thus, there are 100 employees who are females with advanced degrees. Answer = (C).
3) This problem calls for a 3×3 double matrix. Here are the numbers for the grade levels, with the column totaled:
Obviously, 10% of 400 is 40, so 30% is 3*40 = 120, and 60% = 6*40 = 240. This allows us to complete the bottom row.
All 40 from C are freshmen, so we can put zeros in the other two grade level slots:
Half of the 120 from B, 60, are upperclassmen, and the other 60 are evenly split, 30 in each of the other two slots.
Now, we can complete the sophomore row:
There are 70 sophomores from A. Answer = (B).
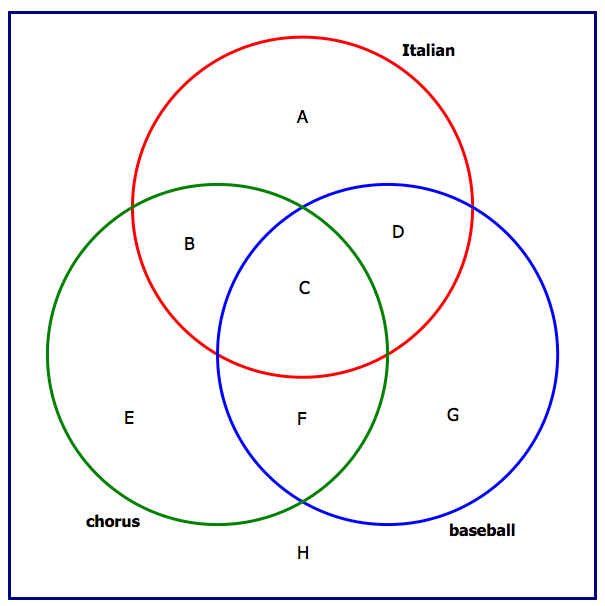
4) This problem calls for a 3-way Venn Diagram. Here’s the diagram with no numbers filled in.
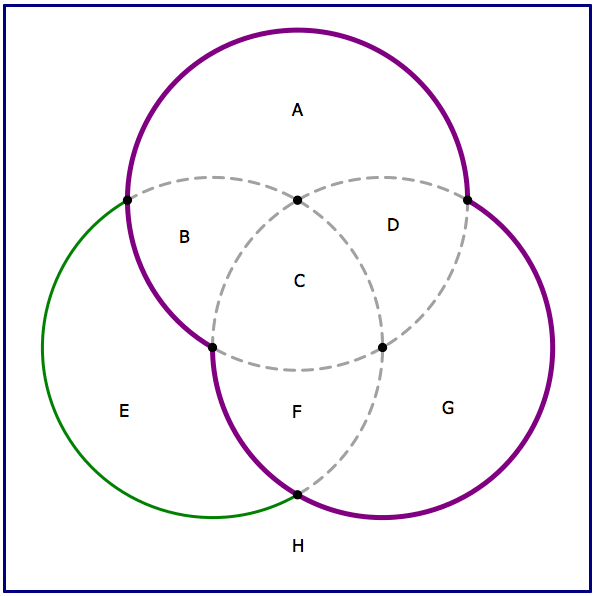
We know that C = 15. If 40 students are in both chorus & Italian, B + C = 40, and because C = 15, B = 25. If 45 students in both chorus & baseball, C + F = 45, and F = 30. We know that there are 120 in chorus, and B + C + F = 70, so E = 50.
Now, we are told that 220 student are in either Italian or baseball. Think about that region, Italian or baseball:
That entire purple region, A + B + C + D + F + G, is 220. If we add E = 50, that’s a total of 270 inside all three circles, which means that the outside of the circle, H, must equal 400 – 270 = 130. Answer = (E).
















Leave a Reply