Comparing Ratios on the GMAT

Among other things, this post is a case study of an OG DS question:

OG 12th Edition, Data Sufficiency Practice Problem #23

Here is the problem that appears in the OG:

23) If p₁ and p₂ are the populations and r₁ and r₂ the number of representatives of District 1 and District 2 respectively, the ratio of the population to the number of representatives is greater for which of the following districts?

(1) p₁>p₂

(2) r₂>r₁

(A) Statement 1 alone is sufficient but statement 2 alone is not sufficient to answer the question asked.

(B) Statement 2 alone is sufficient but statement 1 alone is not sufficient to answer the question asked.

(C) Both statements 1 and 2 together are sufficient to answer the question but neither statement is sufficient alone.

(D) Each statement alone is sufficient to answer the question.

(E) Statements 1 and 2 are not sufficient to answer the question asked and additional data is needed to answer the statements.

Below, I’ll show the solution to this.

Basic Fraction Facts

Here are two very important fraction rules.

1) When the numerator increases and the denominator stays the same, the fraction as a whole increases.  When the numerator decreases and the denominator stays the same, the fraction as a whole decreases.

2) When the denominator increases and the numerator stays the same, the fraction as a whole decreases.  When the denominator decreases and the numerator stays the same, the fraction as a whole increases.

Those, as they are stated, are always true 100% of the time.

Not As Simple

If both the numerator and denominator change at the same time, then things are trickier.  See the table below, which assumes that both numerator and denominator are positive.

In the first case, for example, whether the fraction increases depends on how much the numerator increases, and how much the denominator increases.  For example:

1/3 -> 2/5   both numerator & denominator increase, and fraction increases

1/3 -> 2/7   both numerator & denominator increase, and fraction decreases

(Both of those can be easily seen from the fact that 1/3 = 2/6, so be increasing or decreasing the denominator of 2/6, we can create bigger or smaller fractions.)

Back to the OG DS Problems

Now, we can tackle the DS problem above.  We are comparing fractions of population over number of representative, p/r.

Statement #1: The numerator of the first fraction is larger.  If we knew the denominators were staying the same or getting smaller, we could deduce that the fraction overall is getting bigger.  Unfortunately, we have no information about how the denominators compare.  Statement #1, by itself is insufficient.

Statement #2: As always in GMAT DS question, we have to forget about everything in Statement #1 and focus only on what Statement #2 says.  — We know the second fraction has a lager denominator.  We have no information now about the numerators.  Statement #2, by itself is insufficient.

Statements #1 & #2 combined: Now, we know that when we go from the first fraction to the second fraction,

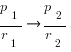
the numerator decreases and the denominator increases.  This is row three of the table above: the fraction as a whole decrease, so District #2 has a lower population to representative ration than District 1.  Answer = C

Here’s another GMAT Data Sufficiency Question on ratios, to practice: http://gmat.magoosh.com/questions/995