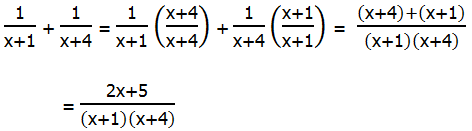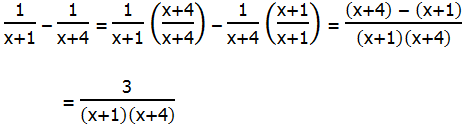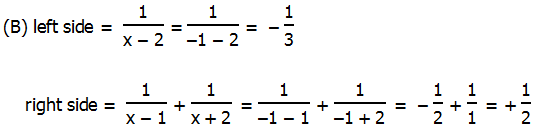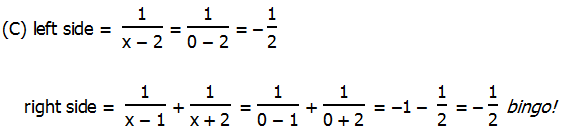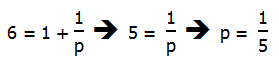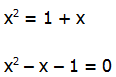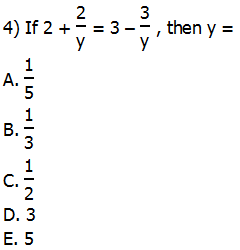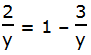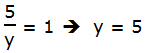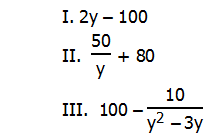Algebraic equations with fractions, more formally known as “rational expressions,” appear in some of the most challenging GMAT algebra questions in the Quant section. These are called “rational” in the sense of “having to do with a ratio”, as the word is used in the phrase “rational numbers“.
Itching to get practicing? Click here to go straight to the practice problems.
Thoughts on Algebraic Equations with Fractions
First of all, to understand this stuff, you should be clear on the basic rules of fractions: how to add, subtract, multiply, and divide them. If you can’t do this basic arithmetic with numerical fractions, it will be very hard to do it with algebraic rational expressions! Some further tips:
1. Suppose you have an equation involving one or more algebraic rational expressions. Suppose you are asked to solve for values of the variable. It’s important to note that any value of the variable that makes any individual denominator equal to zero cannot possibly be a solution of the equation. This can be a powerful tool in “which of the following could be a solution” question, because usually you can immediately eliminate a few answers right away, which sets you up very well for backsolving or solution behavior.
2. When adding or subtracting rational expressions, as when adding or subtracting ordinary fractions, we must find a common denominator to combine. We must do precisely the same thing with rational expressions. Here are a couple examples of this process.
Example #1
Example #2
3. Whenever you have just one algebraic fraction on one side of the equation equal to just one algebraic fraction on the other side of the equation, then you can cross-multiply. If either side has more than one fraction, added or subtracted, you would have to combine them, via the previous hint, before you are ready to cross-multiply.
4. If the whole equation has only one or two denominators, you also can simply multiply every term on both sides by the denominators. That can be a very efficient way to get rid of all the fractions in one fell swoop. For example, the equation:
can be simplified by multiplying each term by (x – 2) —- with the fraction, it cancels the denominator, simply leaving the numerator.
x(x – 2) = 2(x – 2) + 1
If we were to multiply this all out, we would get a quadratic that we could solve.
5. One could always use a direct algebraic solution: that may be efficient or that may take several steps and be time-consuming, even if you know you are doing. Remember that backsolving may be quicker. For a compound fraction (a big fraction with a little fraction in the numerator or denominator), it may well be quicker to step back and perform a more holistic solution, looking at what must be true about each piece: I demonstrate this in the solution for practice problem #2.
Practice Round 1: Solving Algebraic Equations with Fractions
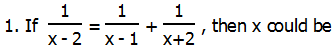
-
(A) –2
(B) –1
(C) 0
(D) 1
(E) 2
Show Answer and Explanation
We could multiply by the three denominators, (x – 2), then (x – 1), then (x + 1), get three quadratics, and simplify. That’s a lot of work.
We could find a common denominator on the right, combine them into a single ugly fraction, then when we had a single fraction on each side, we could cross multiply. That’s also a lot of work.
The simple solution for which this problem is crying out is backsolving. Notice that three of the answer choices — (A) & (D) & (E) — are illegal because each makes one of the denominators zero. We can immediately eliminate all three of those. Now, it’s just a matter of plugging in the other two answer choices.
The two sides are not equal, so (B) can’t be the right answer. At this point, we pretty much know that (C) must be the answer, but it’s always good to verify that it works.
Both sides are equal, so x = 0 satisfies this equation. Therefore, answer = (C).
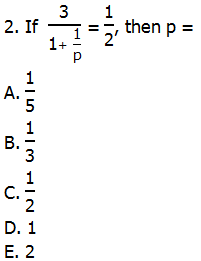
Show Answer and Explanation
Rather than do a ton of algebraic re-arranging, let’s think about this. We have 3 divided by (something) equals 1/2. This means, the “something” must equal 6. That immediately produces the much simpler equation:
Answer = (A)
![]()
-
(A) zero
(B) one
(C) two
(D) a finite number greater than two
(E) infinitely many
Show Answer and Explanation
Multiply all three terms by x and we get
This equation is unfactorable. It is not a perfect square. Think about its graph, which is a parabola:
When x = 0, y is negative, and when x = 2, y is positive. Therefore, the parabola intersects the x-axis twice, which means the equation has two real solutions.
Answer = (C).
BTW, this is a special mathematical equation. One solution is the Golden Ratio, and the other solution is the negative reciprocal of the Golden Ratio.
Show Answer and Explanation
This is an easy one to solve. Subtract 2 from both sides:
Now, add 3/y to both sides. Because the two fractions have the same denominator, y, we can just add the numerators:
Answer = (E)
5. As y increases from y = 247 to y = 248, which of the following decreases?
-
(A) I only
(B) II only
(C) III only
(D) II and III only
(E) I, II, and III
Show Answer and Explanation
As y gets larger, what happens to each one of these?
For statement I, as y gets larger, the 2y gets larger. Since the subtracting 100 stays the same as the value of y changes, that makes no difference. This one increases as y increases, so it is not a correct choice.
For statement II, as the denominator of a fraction increases, the value of the fraction overall decreases. When y increases, 50/y has to decrease. Again, adding 80 remains the same as y changes, so this doesn’t make any difference. This is a correct choice.
For statement III, as long as y > 3, then y^2 – 3y will increase as y increase. That means the entire fraction decrease. We are subtracting 100 minus the fraction, and if the fraction gets smaller, then we are subtracting something smaller and therefore are left with more. This means the entire expression, the difference, gets bigger as y increase. This one increases as y increases, so it is not a correct choice.
Answer = (B)
You’ve reached the end of practice round 1! Grab a snack, get up and stretch, then get ready for practice round 2 for algebraic equations with fractions.
Practice Round 2: Manipulating Algebraic Equations with Fractions
This next set of practice problems and explanations takes you through a range of scenarios you might encounter on GMAT Math. If you’re looking to practice specific areas, feel free to jump around. But if you’re still struggling to apply what you’ve learned about algebraic equations with fractions to actual problems, be sure to tackle the problems and explanations in order.

Show Answer and Explanation
Expressions
Let’s begin with “Do what’s mathematically sound.” When you multiply through by a common denominator, you’re changing the value of every single term (except when the term is equal to zero or the denominator is equal to one). That’s okay when you’re dealing with an equation, so long as you do exactly the same thing to both sides of the equation, but it’s not okay when you’re asked to evaluate an expression.
It may be tempting to multiply through by 10, the least common denominator, but that will yield an answer ten times too great. Instead, take a look at the answers to see what form they take, and manipulate the expression toward answers of that form. It looks as though we’ll want to get the m and n denominators together. We can accomplish this by giving them a common denominator. In this case, that means multiplying the term \( m/5 \) by \( 2/2 \), to get \( {2m}/10 \). Notice that this effectively multiplying \( m/5 \) by 1. The single most commonly useful way to manipulate an expression is to multiply it by 1.
![]()
Since the two terms now have the same denominator, we can join the numerators.
![]()
If it not clear how to translate that further, then rewrite it as,
![]()
Since 1/10=0.1, you can finally rewrite the expression in the useful form.
0.1(2m+n)
Before we turn to the more interesting cases, let’s be reiterate explicitly the lessons we can draw from this example:
- You can’t multiply through by a common denominator unless you have an equation.
- It’s often useful—especially when you’re asked to evaluate an expression—to see what form the answers take.
- The single most commonly useful way to manipulate an expression is to multiply it by 1.
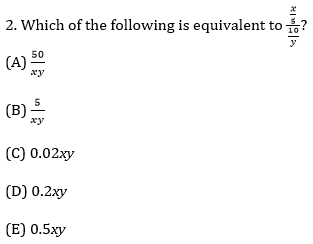
Show Answer and Explanation
Expressions Pt. 2
Because this is an expression rather than equation, we don’t have the option of multiplying through by a common denominator. What could we do? Well, as we saw in our last post, the single most commonly useful way to manipulate an expression is to multiply it by 1. But wait! Isn’t there a standard way to manipulate a compound fraction? Should we use that instead?
Yep, and as we’ll see, that standard way to manipulate a compound fraction is just one way to multiply the expression by 1.
You may remember that the standard way to divide by a fraction is to multiply by the reciprocal of that fraction; lots of American students learn this as “invert (the denominator) and multiply (by that inverse).” That mnemonic works well enough, but it may obscure the underlying logic.
Let’s go ahead and manipulate for now, and then double back and tackle the underlying logic. Let’s rewrite the problem so that we’re multiplying the numerator (x/5) by the reciprocal of the denominator:
\({x/5}/{10/y}\) becomes \({x/5} x {y/10}\) which in turn becomes xy/50.
As with the problem from my last post, we’d better take a look at the answer choices to see what form our expression should take. We’re going to want it in the form of answers C, D, and E: a decimal fraction multiplied by the expression .
If you can’t translate automatically, do it in stages:
xy/50
\( {(1/50)}(xy) \)
\( {(2/100)}(xy) \)
(0.02)(xy)
0.02xy
Remember that I wrote above that multiplying by the reciprocal (or “inverting and multiplying”) is just a special way of multiplying by 1? Let’s see why.
Consider the general form \({a/b}/{c/d}\). We could simplify this fraction by multiplying by a special form of 1, \({d/c}/{d/c}\):
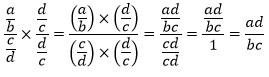
Of course, that’s the very same result that you’d get by going directly to “invert and multiply.” Fortunately, if you’re well-practiced with that maneuver, you don’t need to worry about the underlying logic during the test.
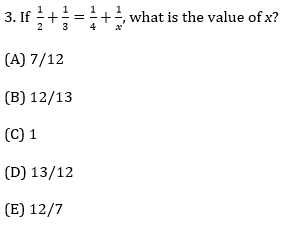
Show Answer and Explanation
Equations
This is where we turn from “Do what’s mathematically sound,” to “Do what’s useful.”
When you’re solving an algebraic equation, what’s generally useful is to clear away all the grouping symbols, that is, the parentheses, division bars, and radical signs. Doing so allows you to move around the variables and constants in whatever way you like. There will be exceptions, but your default move when you see an algebraic equation with fractions should be to multiply every term by the least common denominator to clear the fractions, thus clearing grouping symbols.
A Nice Efficient Solution
Multiply each term by the least common denominator, 12x.
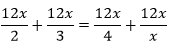
Next simplify each expression.
![]()
Once you’ve cleared the grouping symbols, you’re much more likely to be able to solve the problem. In this case, we’ll transpose, subtracting 3x from each side of the equation.
![]()
Finally , we’ll divide each side by 7 to get,
![]()
A Messy Solution that Invites Error
I’ve often seen students tackle problems like this by treating the expressions on each side of the equal sign as inviolate. That is, many students begin by adding:
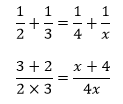
This might work out alright for you in the end—there’s certainly nothing in these operations—but it’s just not very useful.
Another Solution that’s Not Quite As Messy
The same is true to a lesser extent for the method that begins by transposing to isolate the x term:
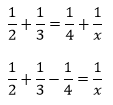
If you followed this step by immediately clearing the fractions, no harm done. Unfortunately most people who begin this way instead proceed to simplify the left hand side of the equation:
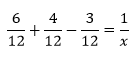
Again, this could work out alright, but a surprisingly large number of people who start this way choose answer
Take-Aways
- If the question gives you an equation, it’s almost certainly easiest to do the same the thing to both sides of the equation, rather than to simplify the expressions on each side of the equation.
- If that equation includes grouping symbols—parentheses, division bars, radical signs—it’s usually simplest to begin by getting rid of those grouping symbols.
4. Little Texas Drilling Company has three wells, each producing oil at a constant rate. Well A produces one barrel every two minutes. Well B produces one barrel every three minutes. Well C produces one barrel every four minutes. How many hours does it take Little Texas Drilling Company to produce 195 barrels of oil?
(A) 2
(B) 3
(C) 4
(D) 18
(E) 180
Show Answer and Explanation
Word Problems
All the problems we’ve so far considered have presented as algebra. However, quite a few word problems translate into algebraic equations with fractions. In particular, some of the hardest work-rate problems become very easy if you can correctly translate them into algebraic equations with fractions, and then correctly solve those equations.
A combined rate problem that asks about simultaneous action allows a nice shortcut. If every worker starts and stops at the same time or is working continuously for the duration of the story, we can simply add the various work rates together to determine the combined work rate. Be sure to express work rates as work/time, and be careful to use the same units throughout the problem.
In this case, the rate for Well A is 1/2 (one barrel/two minutes), for Well B 1/3, and for well C 1/4. The combined rate is 195 barrels in x hours, which we can express as 60x minutes.
All that remains is to solve for x.
Multiply through by 60x to clear the fractions.
30x + 20x + 15x = 195
Combine like terms.
65x = 195
And divide each side of the equation by 65.
x = 3
The answer, therefore, is (B).
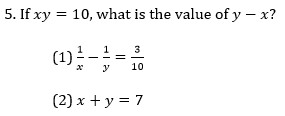
(A) statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question
(B) statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer the question
(C) both statements taken together are sufficient to answer the question, but neither statement alone is sufficient
(D) each statement alone is sufficient
(E) statements 1 and 2 together are not sufficient, and additional data is needed to answer the question
Show Answer and Explanation
System of Equations
Things can get a little more complicated in the Data Sufficiency format, because questions in that format often present us with systems of equations.
It’s tempting to suppose that the correct answer is D, since the “if” statement provides one equation and each of the numbered statements provides an equation. However, it’s not the case that just any pair of equations yields values for two variables. The rule is that to solve for two (or n) variables requires two (or n) distinct linear equations. In this case, the equation xy=10 is not linear.
Let’s suppose that you decided to start with Statement (2). Before solving algebraically for the values of the variables (which approach would require first constructing and then solving a quadratic equation), check whether simple integer values fit both Statement (2) and the “if” equation. After all, the GMAT usually uses pretty manageable values, and there are too many possibilities for the two relevant simple equations.
In fact, it looks as though x and y could be 2 and 5. But which is which? Since y -x could be either 5-2 or 2-5, Statement (2) is not sufficient. Eliminate answers B and D.
Statement (1) is more interesting still. In the last post in this series I wrote that when faced with an algebraic equation involving fraction, you should generally multiply through by the least common denominator to clear all the fractions. Questions which ask you for the value of an expression with more than one variable are sometimes exceptions. In this case, for instance, it’s likely easier to solve for y – x
directly than for y and x separately.
This means that rather than multiply through by 10xy to clear the fractions, we should manipulate the equation to isolate y – x.
![]()
Cross multiply the terms on the left-hand side of the equation.
![]()
Multiply each side of the equation by xy to clear the fraction on the left-hand side.
![]()
It looks as though our question, “What is y – x?”is equivalent to the question, “What is xy?” Since Statement (1) provides and answer to that question, Statement (1) is sufficient.
The correct answer is (A).
It turns out that many Data Sufficiency problems with systems of equations work just as this one did.
If you want to try a practice question with explanation from our Magoosh GMAT product, give this a shot.
http://gmat.magoosh.com/questions/137
Other than that, that’s all the practice questions we have for you! If you would like to express anything or ask for clarification, please let us know in the comments section below.