GMAT Math: How to Find the Height of a Triangle?

March 18, 2013

If you have a right triangle and are given two sides and would like to find the third, use the Pythagorean Theorem: $a^2+b^2=c^2$.

Suppose you need to know how to find the height of a triangle △ABC given 3 sides, {6,7,8}.

This is a question some GMAT test takers ask. They know they would need the height to find the area, so they worry: how would I find that height.

The short answer is: forget about it!

Height of a triangle: which height?

I don’t mean to be flippant. It’s just that first of all, the “height” of a triangle is it’s altitude. Any triangle has three altitudes, and therefore has three heights! Confusing? I know, sorry.

You see, any side can be a base. From any one vertex, you can draw a line that is perpendicular to the opposite base — that’s the altitude to this base.

Any triangle has three altitudes and three bases.

You can use any one altitude-base pair to find the area of the triangle, via the formula $A= \frac{1}{2}bh$.

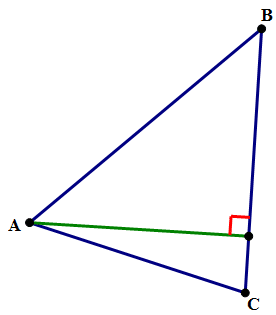
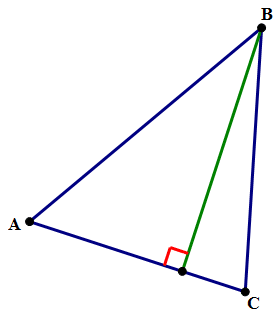
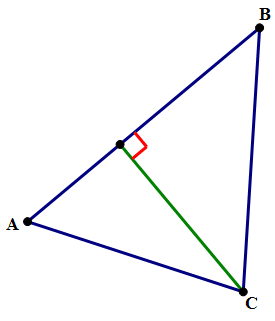
In each of the diagrams above, the triangle ABC is the same. The green line is the altitude, the “height”, and the side with the red perpendicular square on it is the “base.” All three sides of the triangle get a turn.

Finding a height

Given the lengths of three sides of a triangle, the only way one would be able to find a height and the area from the sides alone would involve trigonometry, which is well beyond the scope of the GMAT.

You are 100% NOT responsible for knowing how to perform these calculations. This is several levels of advanced stuff beyond the math you need to know. Don’t worry about that stuff.

In practice, if the GMAT problem wants you to calculate the area of a triangle, they would have to give you the height.

The only exception would be a right triangle — in a right triangle, if one of the legs is the base, the other leg is the altitude, the height, so it’s particularly easy to find the area of right triangles.

What you need to know

You need to know basic geometry. Yes, there is tons of math beyond this, and tons more you could know about triangles and their properties, but you are not responsible for any of that. You just need to know the basic geometry of triangles, including the formula:
$A = \frac{1}{2} b h$

If the triangle is not a right triangle, you have absolute no responsibility for knowing how to find the height — it will always be given if you need it.

Here’s a free practice question for you.

Two sides of a triangle have length 6 and 8. Which of the following are possible areas of the triangle?

2
12
24

Click here for the answer and video explanation!

Some “more than you need to know” caveats

If you don’t want to know anything about this topic that you don’t absolutely need for the GMAT, skip this section!

Technically, if you know the three sides of a triangle, you could find the area from something called Heron’s formula, but that’s also more than the GMAT will expect you to know.

If one of the angles of the triangle is obtuse, then the altitudes to either base adjacent to this obtuse angle are outside of the triangle.

Super-technically, an altitude is not a segment through a vertex perpendicular to the opposite base, but instead, a segment through a vertex perpendicular to the line containing the opposite base.

In the diagram above, in triangle △DEF, one of the three altitudes is DG, which goes from vertex D to the infinite straight line that contains side EF. That’s a technicality the GMAT will not test or expect you to know.

If the three sides of a triangle are all nice pretty positive integers, then in all likelihood, the actual mathematical value of the altitudes will be ugly decimals.

Many GMAT prep sources and teachers in general will gloss over that, and for the purposes of easy problem-solving, give you a nice pretty positive integer for the altitude also.

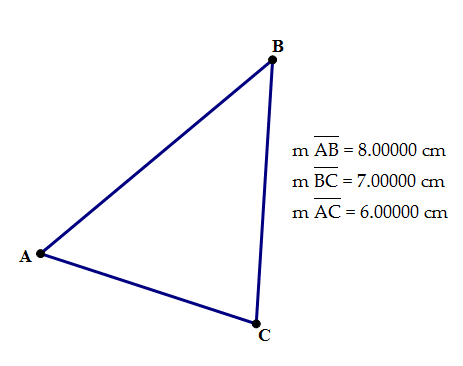
Remember this triangle △ABC from above?

For example, the real value of the altitude from C to AB in the 6-7-8 triangle is:

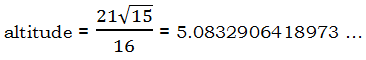
Not only are you 100% NOT expected to know how to find that number, but also most GMAT practice question writers will spare you the ugly details and just tell you, for example, altitude = 5.

That makes it very easy to calculate the area.

Yes, technically, it’s a white lie, but one that spares the poor students a bunch of ugly decimal math with which they needn’t concern themselves.

Actually, math teachers of all levels do this all the time — little white mathematical lies, to spare students details they don’t need to know.

So far as I can tell, the folks who write the GMAT itself are sticklers for truth of all kinds, and do not even do this “simplify things for the student” kind of white lying.

They are more likely to circumvent the entire issue, for example, by making all the relevant lengths variables or something like that.

Takeaways

Still with me?

Here’s what you need to know about triangles on GMAT test day:

$Area =\frac{1}{2}bh$
You’ll only need to know the height of right triangles on the GMAT
If it’s not a right triangle, you’ll be given the height
Know all three angles and two sides? Use the Pythagorean theorem

If you like more free resources (who doesn’t?), or are simply wondering what the GMAT test content is going to be like, check out our Complete Guide.

You’ve got this.

If you have any questions, let me know in the comments below. And yes, I read every single one of them!

Author

Mike MᶜGarry

Mike served as a GMAT Expert at Magoosh, helping create hundreds of lesson videos and practice questions to help guide GMAT students to success. He was also featured as “member of the month” for over two years at GMAT Club. Mike holds an A.B. in Physics (graduating magna cum laude) and an M.T.S. in Religions of the World, both from Harvard. Beyond standardized testing, Mike has over 20 years of both private and public high school teaching experience specializing in math and physics. In his free time, Mike likes smashing foosballs into orbit, and despite having no obvious cranial deficiency, he insists on rooting for the NY Mets. Learn more about the GMAT through Mike’s Youtube video explanations and resources like What is a Good GMAT Score? and the GMAT Diagnostic Test.

View all posts

Share2

Tweet1

Comments

32 responses to “GMAT Math: How to Find the Height of a Triangle?”

Stephanie Whatley

August 7, 2019

how do you find the height when the triangle’s base is 54cm, and the two sides are both 55cm

Reply
1. David Recine
  
  August 13, 2019
  
  In that case, the best thing is to divide the triangle in 2 by drawing a straight line down from the vertex to the two equal sides to the center of the base. From there, you need to use the Pythagorean theorem to calculate that middle line, which creates two right triangles. To show you how, I’ll quote an earlier comment under this article form one of our test prep experts (with modifications made to account for your slightly different triangle:
  
  “So all you need to do is calculate that middle line. How? By using the a^2 + b^2 = c^2 formula, the Pythagorean theorem. Recall that this theorem states that when you have a right triangle, (side 1)^2 + (side 2)^2 = (3rd side that’s on the right angle)^2. So if you have the length of two equal sides of a triangle, you have (55)^2 + [(1/2)*54]^2 = height. Side 2 will be 1/2 of 54, because it will be the 54 cm base, cut in half.”
  
  Reply
Iced Hercules

February 5, 2019

Can u please say me.the formula for finding the height of a equilateral triangle…

Reply
1. Magoosh Test Prep Expert
  
  February 6, 2019
  
  Certainly! When you have an equilateral triangle, you can divide it in half to make two right triangles. The line that divides the equilateral triangle in half will be the shared side of the two right triangles. That line will also be the height of the equilateral triangle.
  
  So all you need to do is calculate that middle line. How? By using the a^2 + b^2 = c^2 formula, the Pythagorean theorem. Recall that this theorem stats that when you have a right triangle, (side 1)^2 + (side 2)^2 = (3rd side that’s on the right angle)^2. So if you have the length of the sides of the equilateral triangle, you have (length)^2 + [(1/2)*length]^2 = height. Side 2 will be 1/2 the usual length, because it will be the side of one of the right triangles that you create when you cut the equilateral triangle in half.
  
  I hope this helps. But if you still have doubts, feel free to post a follow-up content. You can also read more on this in Magoosh’s post about the Pythagorean theorem on the GMAT.
  
  Reply
Evie

May 20, 2018

Hey, I was having a bit of trouble with a maths question and I’m hoping you could help me out:

It’s an equilateral triangle where all the sides are x. The area is 36cm2. I have to find x.

Thanks in advance!

Reply
1. Magoosh Test Prep Expert
  
  May 25, 2018
  
  Hi Evie,
  
  Unfortunately, we aren’t able to help with questions from outside materials. We’re a small team and must prioritize GMAT questions from our own produce and those from Official materials. If this is a question from one of those sources, please let me know!
  
  In the meantime, I highly recommend that you check out the Khan Academy videos that discuss the area of equilateral triangles and the relationships between the sides of the triangle and it’s area.
  
  Reply
2. SHIVAM DHAWAN
  
  October 9, 2018
  
  Formula for the Area of equilateral triangle is = √3/4 x^2
  √3/4 x^2 = 36
  Equate and find the value.
  
  Reply
medo

March 13, 2018

Two of the altitudes of a triangle are 10 cm and 11 cm. Which of the following cannot be the length of the third altitude? (A) 5 cm. (B) 6 cm. (C) 7 cm. (D) 10 cm. (E) 100 cm. 27.

Reply
1. Magoosh Test Prep Expert
  
  March 13, 2018
  
  As mike mentioned, this is beyond the scope of the GMAT… or the kind of math support generally provided by the Magoosh GMAT Blog. However, there is a good discussion thread on this type of math problem over at the Art of Problem Solving website. Check it out. 🙂
  
  Reply
Simran

October 16, 2017

Hi ,
can anyone solve this question please?
If area of triangle is 42 what will be its base and height

Reply
1. Magoosh Test Prep Expert
  
  October 18, 2017
  
  Hi Simran,
  
  There is not enough information to solve this. There are infinitely many triangles that would satisfy this requirement. 🙂
  
  Reply
2. mdot
  
  February 8, 2018
  
  Base = 6
  
  Height – 14
  
  Reply
  1. Magoosh Test Prep Expert
    
    February 9, 2018
    
    That is one possibility, but there could also be many others. Base 42 and height 2, base 21 and height 4, and so on.
    
    Reply
Mancha

August 23, 2016

How do you get the perependicular hight of they have given you all three sides of the triangle

Reply
1. Magoosh Test Prep Expert
  
  August 27, 2016
  
  Hi Mancha,
  
  In many cases, finding the perpendicular height of a triangle involves trigonometry which is not covered on the GMAT. As Mike says in this post: “In practice, if the GMAT problem wants you to calculate the area of a triangle, they would have to give you the height. The only exception would be a right triangle — in a right triangle, if one of the legs is the base, the other leg is the altitude, the height, so it’s particularly easy to find the area of right triangles.”
  
  So you will basically only have to be able to solve for the height of a right triangle using the pythagorean theorem. You should also check out the “More than you need to know caveats” section of this blog for some other information 🙂
  
  Reply
  1. Zamokuhle
    
    August 20, 2017
    
    I’m actually doing trigonometry and I’m faced with the same problem discussed where can i get a thorough explanation on how to solve this its an assignment so asking the teacher is out of the equation
    
    Reply
    1. Magoosh Test Prep Expert
      
      August 25, 2017
      
      Hi Zamokuhle,
      
      Have you heard of Khan Academy? They have thousands of excellent video and practice resources to help you understand these sorts of questions and how to answer them! Our website mainly focuses on preparation for standardized tests, so it may not help you as much in your trig class. Khan Academy, however, was made to help students like you learn and succeed. Check it out!
      
      Reply
Cecy

June 29, 2016

What about if you are given one side but no base nor height? DEF and one side is 6cm the other two are not given and you need to find the area of the triangle.

Reply
1. Magoosh Test Prep Expert
  
  July 3, 2016
  
  Hi Cecy,
  
  Happy to help! 🙂
  
  If you only have the measure of one side of a triangle, you cannot solve for the area. The GMAT does not typically wander into trigonometry, but even if we applied concepts from trig, you could not solve with just the measure of one side. The minimum information you need (besides the base and height we use in the basic geometry formula) would be all three side measures (to use Heron’s formula) or else angle-side-angle or side-angle-side.
  
  In short, the problem you propose is impossible. I hope this clarifies!
  
  Reply
Diana

June 5, 2016

please can you say me — base multiplied by height is equal to 2 multiplied by what? of a triangle

Reply
1. Magoosh Test Prep Expert
  
  June 6, 2016
  
  For a triangle, the area of the triangle, multiplied by 2 is equal to the base of the triangle times the height. Written as a formula, this would be 2A=bh for a triangle. This equation can help you find either the base or height of a triangle, when at least one of those two variables is given.
  
  A useful flip side of this formula is (1/2)bh = the area of a triangle. So if you already have the values for a triangle’s base and height, you can get the area of the triangle.
  
  Reply
Nathan Peterson

April 10, 2016

I am in Algebra 1, and I am being asked this question on a pop quiz- like homework, and I need to find the height of an isosceles triangle with two sides of 7 units and the base is 8 units.

PLEASE HELP!

Reply
1. Magoosh Test Prep Expert
  
  April 11, 2016
  
  We don’t really offer homework or quiz answers here. And as Mike says, the GMAT doesn’t really do triangle height questions– the height will generally be given. I’ve still decided to approve and reply to your comment Nathan, because you’ve touched on a concept that IS important on the GMAT: The Pythagorean theorem, as it applies to right triangles.
  
  It’s important to remember that any isosceles triangle can be bisected into two right triangles by drawing a straight line from the angle between the two equal sides down to the middle of the base. The vertical line of the right angle on a triangle is considered the triangle’s height as well as its side. And the Pythagorean theorem states that there where a and b are the sides of a right angle on a right triangle and c is the side that is opposite of the right angle on the right triangle, a^2 + b^2 = c^2. Armed with this a squared plus b squared plus c squared formula, you can calculate the missing height of any right triangle as long as you have the length of the other side of the right angle (b^2) and the length of the side opposite the right angle (c^2).
  
  This is important on the GMAT because some exam problems that look like they could be dealing with the unknown height of an isosceles triangle are really asking you to calculate the length of one side of a right triangle, which doubles as the height of an isosceles triangle. And Nathan, this means you can also calculate the height of an isosceles triangle with the Pythagorean theorem by cutting the isosceles in half and treating its height as one side of a right triangle. In the isosceles triangle you described, half the base squared plus 7 squared equals the height!
  
  Reply
Respond Fast Please

February 16, 2016

What is the formula for finding the height of a trapezoid for instance, b1 is 4 b2 is 2.5 and area is 3.9 what is the height?

Reply
1. Magoosh Test Prep Expert
  
  February 20, 2016
  
  Hi there!
  
  The area of a trapezoid is [(a+b)/2]h so if we want to rearrange that to solve for h, we can say that the height is:
  
  Area/[(a+b)/2]
  
  In the case of the numbers you give, that means:
  
  Height = 3.9/[(4+2.5)/2] = 3.9/[(6.5)/2] = 3.9/[3.25] = 1.2
  
  I hope that helps! 🙂
  
  Reply
Maria

December 3, 2015

If I have a triangle with a base of 12 units and two side lengths of 10 units how long will the altitude be?

Reply
1. Manish
  
  January 7, 2016
  
  This is an isosceles triangle which can be cut into 2 right triangles with base as 6 and hypotenuse as 10. So, the 3rd side of the right triangle which also is the altitude of the isosceles triangle is 8.
  
  Reply
Jack

November 12, 2015

If I was given the lengths of a triangle 10, 12, and 15 cm and the area 60 cm how would I find the altitude

Reply
Walter

April 18, 2014

Good day mr. mike.

Can you please prove me wrong that (as i can only verify these in smaller numbers)
If n^2+n is m, and if m is divisible by 3, m is the average of twin primes juxtaposed at m.

Reply
1. Mike
  
  April 19, 2014
  
  Dear Walter,
  I’m happy to respond. 🙂 First of all, rest assured that absolutely no simply algebraic procedure will always generate prime numbers. This has been proven impossible. I would recommend looking at this blog:
  https://magoosh.com/gmat/2013/gmat-quant-must-be-true-problems/
  under the section “Patterns of Prime Numbers.”
  For this, if n = 9, then m = 90, and 91 = 7*13.
  If n = 11, then m = 132, and 133 = 7*19
  If n = 12, then m = 156, and 155 = 5*31
  You see, n^2 + n = n(n + 1) is always even, and if it’s divisible by 3 also, then it has 2 and 3 and 6 as factors, which leaves fewer possible factors for the numbers adjacent to it. That’s why primes are relatively common adjacent to this number, and why we have to go up to n = 18, m = 342, to get to an example that has two non-prime neighbors:
  341 = 11*31
  343 = 7^3
  Does all this make sense?
  Mike 🙂
  
  Reply
walter

April 7, 2014

Mike, i have been solving this problem for weeks and eureka i have solve it fast. this problem is very useful in surveying especially before the advent of high tech electronic gadgets because you have to walk around the perimeter to measure the lenghts so you can get the area bounded. in geometry its called ASA or side angle side and until now, the only way to get altitude is by getting the lenghts of all segments which is way way back to heros time. and i must guess that most of our knowledge of the postulates in geometry eg. concurrence of altitudes of bisectors etc. stems from tinkering with how to find the altitude of the triangle. i was thinking of writing a book about this because the my formula only needs one side and the two angles.

Reply
1. Mike
  
  April 8, 2014
  
  Dear Walter,
  I’m glad you solved your problem. I point out that walking out the perimeter to spec the three sides would determine the triangle via SSS. It’s true that either SSS or ASA or AAS or SAS completely determine a triangle, so any of those should determine the area completely. Frankly, I believe the concurrence of angle bisectors and of medians and etc. was known to Euclid, who didn’t seem particularly concerned with finding altitudes. Nevertheless, the details of geometry are always fascinating to investigate. Best of luck to you.
  Mike 🙂
  
  Reply