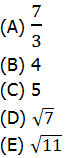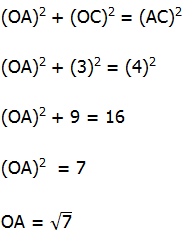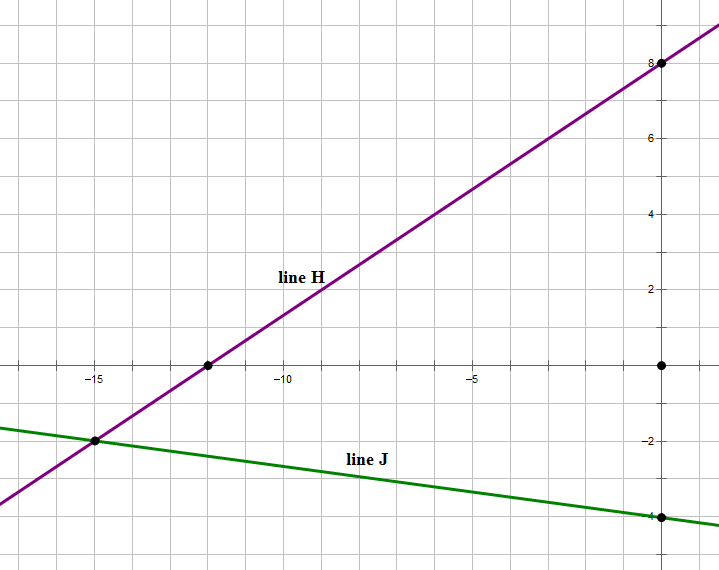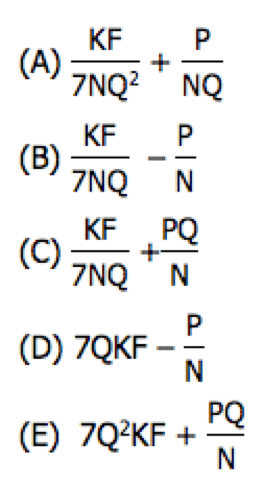GMAT Quant: Coordinate Geometry Practice Questions

For more information on Coordinate Geometry on the GMAT, see these articles:

1) Quadrants in the x-y Plane

2) Special Properties of y = x

3) Slopes

4) Midpoints and Parallel & Perpendicular lines

Here are five new practice problems on these topics.

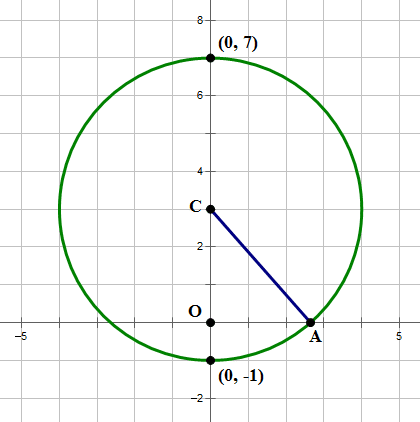
1. The center of circle Q is on the y-axis, and the circle passes through points (0, 7) and (0, –1).  Circle Q intersects the positive x-axis at (p, 0).  What is the value of p?

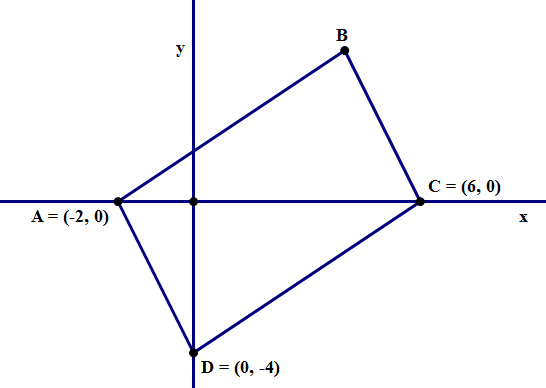
2. In the diagram above, coordinates are given for three of the vertices of quadrilateral ABCD.  Does quadrilateral ABCD have an area greater than 30?

Statement #1: point B has an x-coordinate of 4

Statement #2: quadrilateral ABCD is a parallelogram

3. In the x-y plane, point F = (3, –2).   Point G is at (3, k), where k is an integer such that 5 ≤ k ≤ 40.  If FG is to form the side of a square, how many different square can be created?

(A) 35
(B) 36
(C) 70
(D) 72
(E) 140

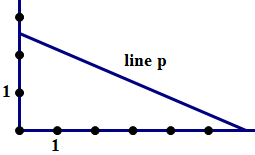
4. In the coordinate system above, which of the following is the equation of line p?

(A) 3x + 7y = 18
(B) 7x + 3y = 18
(C) 3x – 7y = 18
(D) 7x – 3y = 18
(E) 3x + 7y = –18

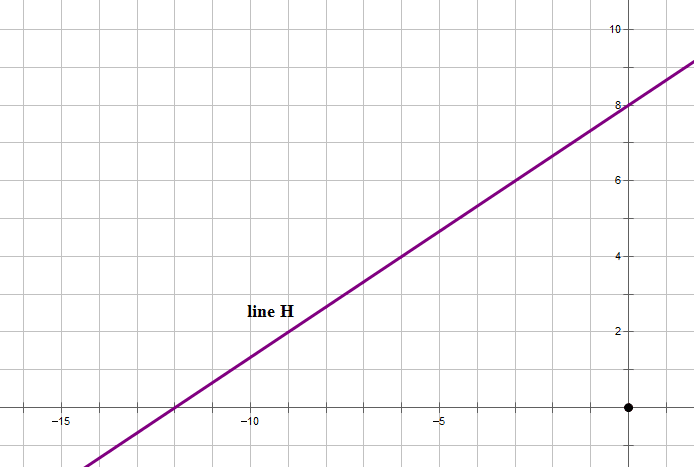
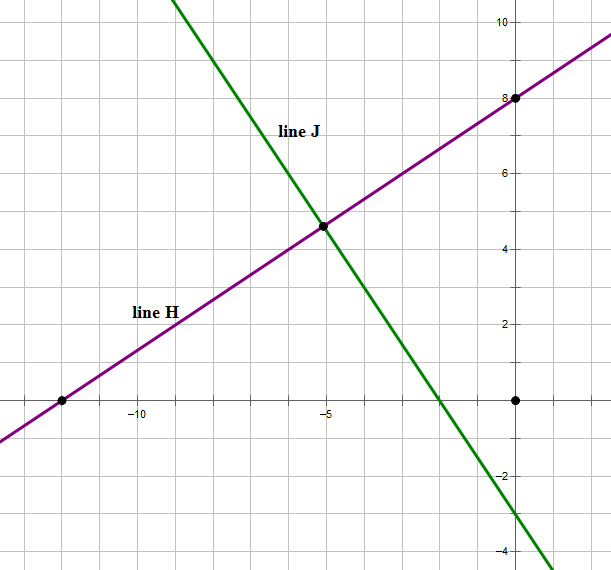
5. The graph above shows line H.  Line J (not shown) does not pass through the first quadrant.  Which of the following could be true?

I.  line J is perpendicular to line H

II.  line J is parallel to line H

III.  line J intersect line H in the third quadrant

(A) I only
(B) II only
(C) I and II only
(D) I and III only
(E) I, II, and III

If would like to express anything, or have any question, please let us know in the comments section below!

Solutions to the Practice Problems

1) The center of the circle must be halfway between (0, 7) and (0, –1), at the point C =  (0, 3).  We know the radius is 4.  Now consider what this looks like:

Here C = (0, 3) is the center.  From C to (0, 7) is a radius of 4, and from C to (0, –1) is also a radius of 4.  Well, AC is another radius, so this also has a length AC = 4.  Notice, now, that OCA is a right triangle.  We know that OC = 3 and AC = 4

Answer = D

2) In this problem, the lower triangle ACD has a base of AC = 8, and a height, from the origin down to D, of 4.  Therefore, the area of ACD = (1/2)(b)(h) = (1/2)(8)(4) = 16.  We would need to know something about the upper triangle ABC to know the answer to the prompt question.  We know the base of triangle ABC, AC = 8, but we don’t know anything about the height.

Statement #1: if we know the x-coordinate of point B, that doesn’t help us.  We still know the base AC = 8, but we don’t know the height, only the vertical line along which point B will lie.  Any height could be possible.  This statement, alone and by itself, is insufficient.

Statement #2: the diagonal of any parallelogram (i.e. the line connecting two opposite vertices) divides it into two congruent triangles.  Well, if ABCD is a parallelogram, then line AC is a diagonal, which means triangles ADC and ABD must be congruent and have equal area.  This would allow us to calculate the total area and answer the prompt question.   This statement, alone and by itself, is sufficient.

Answer = B

3) Idea #1: inclusive counting.   From 5 to 40 inclusive, there are not 35, but 36 values.

Idea #2: The points F & G have the same x-coordinates, so FG must be a vertical segment.

There are 36 possible vertical segments.  Any square with sides parallel to the x- & y-axes has two vertical sides and two horizontal sides.   The vertical segment FG could be the right side or the left side of the square, so for any vertical segment there are two possible squares.

(36 segments) x (2 possible squares) = 72 squares

Answer = D

4) First of all, line p clearly has a negative slope.  If the slope is negative, that means the x & y have opposite sign coefficients when written in slope-intercept form (i.e. y = mx + b).  Thus, if we move the x to the opposite side, so that the x & y are on the same side, then they will have to have the same sign coefficients.  The x & y coefficients could be both positive or both negative.  The latter is not an option among the answer choices.   We must have a plus-sign, so answers (C) & (D) are out right away.

Notice the x intercept is approximately (6, 0) —- it could be exactly equal to that, or approximately equal to that.  Plug this in to the three remaining choices, and see what happens.

(A) 3(6) + 7(0) = 18 YES, exactly true

(B) 7(6) + 3(0) ≠ 18 no, not even close

(E) 3(6) + 7(0) = –18 no, not even close

Answer = A

5) If line J does not pass through first quadrant, then it must be a line with a negative slope and a negative y-intercept.  Such a line could be perpendicular to line H:

Therefore, Statement I is possible.

Line H has a positive slope, and line J must have a negative slope, so there is absolutely no way for them to have the same slope.  They absolutely cannot be parallel.  Therefore, Statement II is impossible.

Both line H and line J pass through QIII, so there’s no reason they cannot intersect there.  For example:

Therefore, Statement III is possible.

Answer = D

Special Note:

To find out where coordinate geometry sits in the “big picture” of GMAT Quant, and what other Quant concepts you should study, check out our post entitled:

What Kind of Math is on the GMAT? Breakdown of Quant Concepts by Frequency