Fact: On GMAT Problem Solving, some of the prompts will state quantities in terms of variables, and then expect you to answer in terms of those variables. Such questions are known as “variable in the answer choice” questions (or VICs in some circles).
Fact: There are two basic strategies you can use to solve these: (a) a full-on algebraic approach; or (b) plugging in numbers for the variables.
Which of these two approaches is better? Well, we all know your Algebra Two teacher back in high school would have wanted you to pick the algebraic approach — perhaps that teacher even would have considered plugging in numbers a form of “cheating.” BUT — this ain’t high school no more! This is about GMAT, and as in the business world, the guiding principle for getting through the GMAT is: whatever works.
Which of the two approaches is better? It depends entirely on you. This is where you need to practice, trying each approach on questions like this, getting a feel for both approaches, so you develop a sense of which one works better with your style.
An Example Question
As an example, I’ll solve a new question from the OG 13 in both ways. The question is Problem Solving #177 in the 13th edition:
177) Last year the price per share of Stock X increased by k percent and the earning per share increased by m percent, where k is greater than m. By what percent did the ratio of price per share to earnings per share increase, in terms of k and m?
(A) 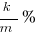
(B) 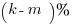
(C) 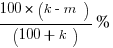
(D) 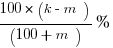
(E) 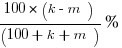
This is a doozy of a question, because there are two variables in the question, and both play a role in the answer. This question is only #177 of 230 PS questions, but it’s one of the hardest questions in that whole section.
Algebraic Approach
First, the approach that would have made your Algebra II teacher happy. This will be hairy. Let price per share be P, and earnings per share be E. Then
original ratio = 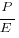
new price per share = 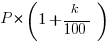
new earnings per share = 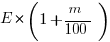
new ratio = (new P)/(new E) =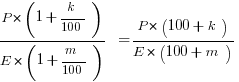
Some comments. Notice that to create the percent increases, I used multipliers. If that’s unfamiliar, it’s a hugely important idea with which you need to acquaint yourself: see this post [https://magoosh.com/gmat/math/understanding-percents-on-the-gmat/]. Now, we need a percent increase from the original ratio to the new ratio. This will be
Percent increase = 
= 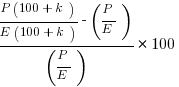
Cancel the factor of P/E everywhere in the fraction
= 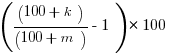
Find a common denominator inside the parentheses.
= 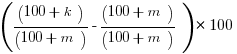
= 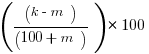
= 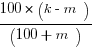
This matches exactly answer D, the correct answer.
Numerical Approach
We need several numbers, which we will pick for ease of calculation rather than for realism. First, say price per share P = 100 (many common stocks are in the ballpark of $100/share) and say that earnings per share is also E = 100 (that’s the part that is unrealistic, but it makes for an easy calculation). The original ratio, P/E = 100/100 = 1.
We need k > m, so let’s say k = 50 and m = 20. Then the new P is 150, the new E is 120, and the new ratio is 150/120 = 15/12 = 5/4.
The change from 1 to 5/4 involves adding a quarter, and a quarter is 25%, so it’s a 25% increase in the ratio. Now, the question is: with values of k = 50 and m = 20, which answer choice gives the correct answer of 25? Before we plug in, we don’t know — it’s possible the values we pick work for two answers: in that case, we would eliminate the cases which didn’t work, then pick new values, and repeat, but only checking the cases that worked the first time.
So, the answers:
(A) k/m % = 50/20% does not equal 25%! Out.
(B) (k – m)% = (50 – 20)% = 30% Out.
(C) 100*(k – m)/(100 + k) % = (100*30)/150 = 3000/150 = 20% Out.
(D) 100*(k – m)/(100 + m) % = (100*30)/120 = 3000/120 = 25% Works.
(E) 100*(k – m)/(100 + k + m) % = (100*30)/170 = 3000/170 = 300/17 = not a whole number, so it certainly doesn’t equal 25. Out.
We got lucky! One choice for the variables was enough to eliminate four of the five, leaving only the correct answer D. In general, if you don’t pick the most obvious choices (k = 200 & m = 100, or k = 100 & m = 50), then you are likely to eliminate four answer choices on your first pick of numbers. That’s one of many reasons it’s an excellent idea to pick less-than-perfectly-obvious numbers when you are taking a numerical approach to a problem like this.
Here’s another question with variables in the answer choices on which you can practice: http://gmat.magoosh.com/questions/325
If you sign up for the Magoosh product, you will get access to this important lesson on problems with variables in the answer choices: http://gmat.magoosh.com/lessons/283-variables-in-answer-choices






Leave a Reply