This post was updated in 2024 for the new GMAT.
Earlier, we featured a blog of Coordinate Geometry practice questions. Here are eight more questions, some of which are challenging.
1) Graph G has a line of symmetry of x = –5/2. Graph G passes through the point (3, 3). What is the x-coordinate of another point that must have a y-coordinate of 3?
(A) –8
(B) –7
(C) –5
(D) –4
(E) 2
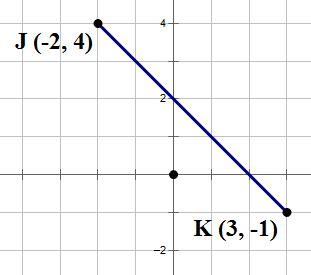
2) In the figure above, the point on segment JK that is four times as far from K as it is from J is:
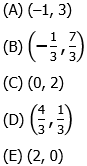
3) Which point is the reflection of the point (–7, 5) over the line y = –x?
(A) (–7, 5)
(B) (–5, 7)
(C) (5, –7)
(D) (7, –5)
(E) (7, 5)
4) In a coordinate system, P = (2, 7) and Q = (2, –3). Which could be the coordinates of R if PQR is an isosceles triangle?
I. (12, –3)
II. (–6, –9)
III. (–117, 2)
(A) I only
(B) I and II only
(C) I and III only
(D) II and III only
(E) I, II, and III
5) Point W = (5, 3). Circle J has a center at point W and radius of r = 5. This circle intersects the y-axis at one intercept and the x-axis at two intercepts. What is the area of the triangle formed by these three intercepts?
(A) 7.5
(B) 12
(C) 15
(D) 24
(E) 30
6) Line M has a y-intercept of –4, and its slope must be an integer-multiple of 1/7. Given that Line M passes below (4, –1) and above (5, –6), how many possible slopes could Line M have?
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10
7) Line Q has the equation 5y – 3x = 45. If Line S is perpendicular to Q, has an integer for its y-intercept, and intersects Q in the second quadrant, then how many possible Line S’s exist? (Note: Intersections on one of the axes do not count.)
(A) 25
(B) 33
(C) 36
(D) 41
(E) 58
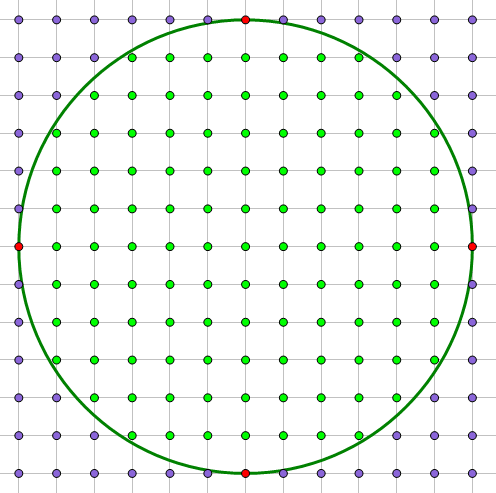
8) In the x-y plane, point (p, q) is a lattice point if both p and q are integers. Circle C has a center at (–2, 1) and a radius of 6. Some points, such as the center (–2, 1), are inside the circle, but a point such as (4, 1) is on the circle but not in the circle. How many lattice points are in circle C?
(A) 36
(B) 72
(C) 89
(D) 96
(E) 109
Some relevant blogs
Here are some blogs that you may find germane. If you look at one of these and have an “aha!”, then you might want to look over these problems again.
2) Special Properties of the line y = x
3) Distance between two points
4) Slopes
5) Midpoints and Parallel & Perpendicular lines
If you found this problems helpful or have a question about any after reading the TE, please let us know in the comments section.
Explanations to the practice questions
1) The line of symmetry is x = –2.5. The point (3, 3) is 3 – (–2.5) = 5.5 to the right of this line of symmetry. It’s reflection must be 5.5 units to the left of the line of symmetry, so (–2.5) – (5.5) = –8 is the x-coordinate. Answer = (A)
2) Call the point P. Then, PK = 4*JP. Of course, JP + PK = JK, so JP + 4*JP = 5*JP = JK, and JP = (1/5)*JK. Point P should be one fifth of the segment away from J. This would be the point (–1, 3). Answer = (A)
3) The point (–7, 5) is in the second quadrant, relatively close to the line y = –x, so the reflection would have to be another point in the second quadrant, and the only answer choice in the second quadrant not equal to the original point is (B), (–5, 7). This question is very easy to solve by visual/spatial reasoning.
For those who want to know the “rule”: when a point is reflected over the line y = –x, the coordinates are reversed, and each one takes on its opposite sign. The –7 becomes +7, and the +5 becomes –5, and they switch places, which also results in (B).
4) Notice that points P & Q are separated by 10 units vertically.
I. R = (12, –3)
Then, point R is 10 units to the right of Q, so we get a big 45-45-90 Right Isosceles Triangle:
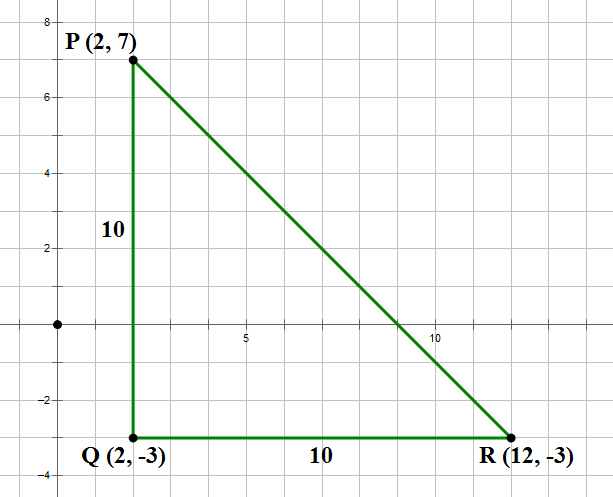
Option I works.
II. R = (–6, –9)
This is tricky. This left 8 and down 6 from Q, so the triangle formed by the x & y separations between Q and this R form a 6-8-10 right triangle, and the distance QR = 10, making this an isosceles triangle as well. This little 6-8-10 triangle on the QR connection is show in dashed lines:
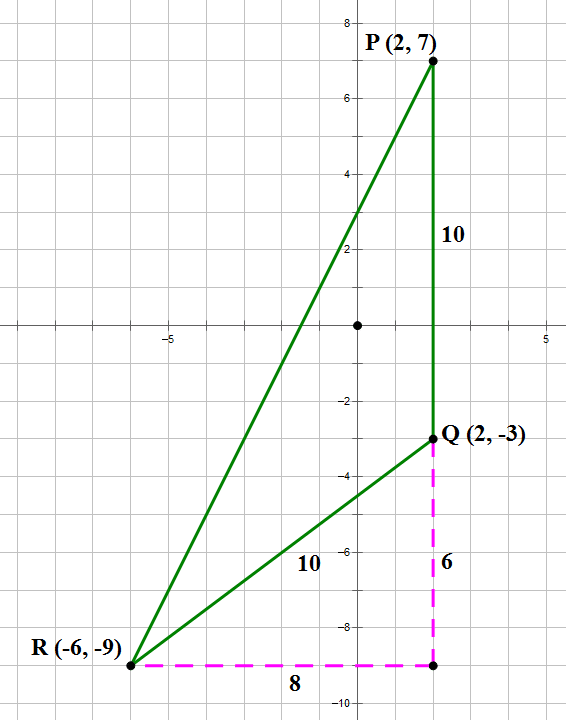
Option II works.
III. R = (–117, 2)
It’s a mistake to do any calculations at all with this one. The line y = 2 is the perpendicular bisector of PQ:
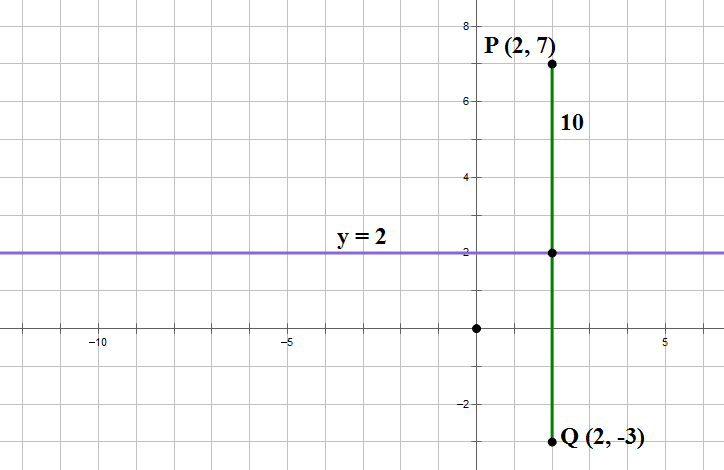
This is an important Geometry idea: any point on the perpendicular bisector of a segment is automatically equidistant from the two endpoints of the segment. This means, we could pick absolutely any point on the line y = 2, call it R, and this point R would be equidistant from P & Q, making PQR an isosceles triangle. The point R = (–117, 2) is on this perpendicular bisector, so it is equidistant from P & Q, and PQR must therefore be isosceles.
Option III works.
Each of the three options works. Answer = (E).
5) Well, if we go 5 units to the left of (5, 3), we’re at (0, 3): that’s the single y-intercept of the circle.
Now, think about the two x-intercepts. Each one is a diagonal distance of r = 5 from (5, 3), and if we may a right triangle on either side, the vertical leg is the distance from (5, 3) straight down to the x-axis, which of course is 3.
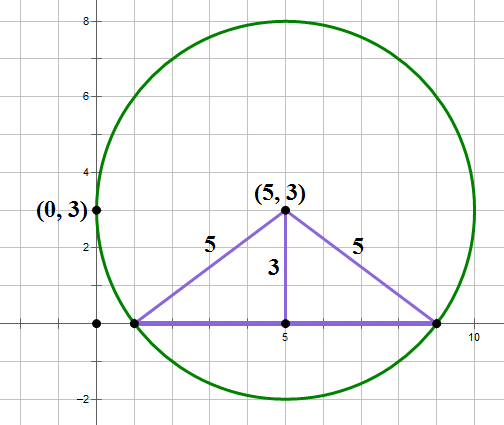
Those two purple triangles must be 3-4-5 triangles, which means each one has a base of 4, and the distance between the two of them is 8. One is at (1, 0) and the other is at (9, 0).
Now, think about the triangle formed by these three intercepts. The base, from (1,0) to (9, 0) is 8, and while the third vertex is off-center, that doesn’t matter — the height is h = 3. A = (0.5)bh = (0.5)(8)(3) = 12. Answer = (B)
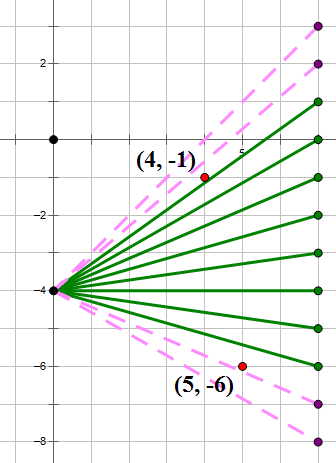
6) Well, for starters, zero is a multiple of every number, and a line with slope zero, the horizontal line y = –4 passes below (4, –1) and above (5, –6). That’s horizontal line is our starting point.
The point (4, –1) is over 4, up 3 from the y-intercept (0, –4). A line with a slope of +3/4 would go straight from (0, –4) to (4, –1). Thus, we need a slope that is less than +3/4. Notice that 3/4 = 21/28. Notice that 5/7 = 20/28, so this would be less than 3/4. Therefore, +1/7 through +5/7 will all slope up, obviously above (5, –6), and all will pass below (4, –1). That’s five upward sloping lines.
The point (5, –6) is over 5, down 2, from the y-intercept (0, –4). A line with a slope of –2/5 would go straight from (0, –4) to (5, –6). Thus, we need a slope that is more than –2/5; another way to say that is, we need a negative slope whose absolute value is less than +2/5. Well, 2/5 = 14/35, while 2/7 = 10/35 and 3/7 = 15/35, so (2/7) < (2/5) < (3, 7). The negatively sloping lines obviously pass below (4, –1), but only two of them, –1/7 and –2/7, pass above (5, –6).
That’s one horizontal line, five upward sloping lines, and two downward sloping lines, for a total of eight. Answer = (C).
7) First of all, Line Q 5y – 3x = 45 re-written in slope-intercept form is y = (3/5)x + 9. Line Q has a y-intercept of +9, so if Line S also has a y-intercept of +9, they would intersect on the y-axis, not in the second quadrant. Therefore, the y-intercept of Line S must be less than 9, and the highest value it could have is a y-intercept of 8.
Now, let’s think about the bottom end. Line Q has a y-intercept of +9 and an x-intercept of –15. Line S, perpendicular to Line Q, must have a slope of –5/3, the negative reciprocal of Line Q’s slope. If we start at the x-intercept of point Q, the point (–15, 0), we would follow the slope of –5/3 over 15 and down 25 to (0, –25). If Line S had a y-intercept of –25, it would intersect Line Q at (–15, 0), on the x-axis, and not in the second quadrant. Therefore, a y-intercept of –25 doesn’t work, and the lowest value that would work is one above it, y-intercept of –24.
Any y-intercept less than or equal to +8 and greater than or equal to –24 would work. That’s 8 positive y-intercepts, the intercept of zero at the origin, and 24 negative intercepts, for a total of 8 + 1 + 24 = 33. Answer = (B)
8) This is a tough question. First of all, obviously, the center a lattice point in the circle. If we move horizontally or vertically, the first 5 lattice points will be inside the circle, and the sixth one will be on the circle, so the points on the circle don’t count as being “in” the circle.
Now, we just are going to focus on one quadrant of the circle, the upper right quadrant. Suppose we go over one unit and up the circle.
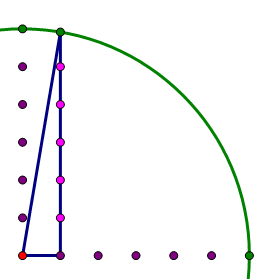
Well, that’s a right triangle, with hypotenuse of r = 6, and horizontal leg of 1, so if the vertical leg is x, then
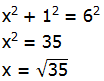
Well, the square root of 35 is bigger than 5, so five points in that column are inside the circle. Now, move two units to the right. Again, hypotenuse r = 6, short leg = 2, vertical leg = x, so
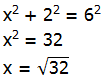
Still bigger than 5, so there five points in this second column. Now, move three units to the right. Again, hypotenuse r = 6, short leg = 3, vertical leg = x, so
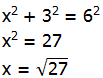
Still bigger than 5, so there five points in this third column. Here’s where we are so far:
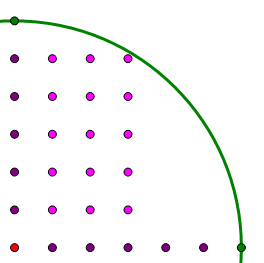
Clearly, by symmetry, we can reflect this array over the 45° line, to get more points in the circle:
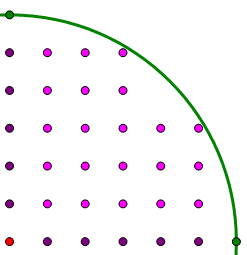
Because that row at a height of 5 only is 3 points wide, we know that the column 5 units to the right can only be 3 points height. We have to check that highest point in the column 4 units to the right. Again, hypotenuse r = 6, short leg = 4, vertical leg = x, so
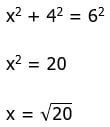
Clearly, this is bigger than 4, so that fourth column can be four points high.
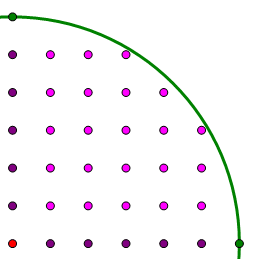
That completes the quadrant. Within the quadrant, that’s 5 + 5 + 5 + 4 + 3 = 22 points. Multiply that by four, and that’s 88 points within the four quadrants. Add the 20 points on the vertical & horizontal segments, and the one point at the center, and we have 88 + 20 + 1 = 109. Answer = (E).