Mathematics is like a foreign language. The unfamiliar symbols are a kind of alphabet, and those symbols combine in peculiar ways according to the mathematical grammar rules of arithmetic, algebra, and other fields of math. In this article we will highlight the essential calculus notation that you’ll need to know for the AP Calculus exam.

Why Does Notational Fluency Matter?
Mathematical notation provides a common language for people to talk about numbers, patterns, and techniques for solving problems.
Just like spoken and written languages, mathematical notation has evolved over the millennia.

It is very important to be fluent in the language of mathematics (notation) in order to fully grasp what’s going on. Otherwise, when it comes time to that the AP Calculus exam, you might feel like a lost tourist trying to make sense of all those foreign street signs.

Free Response Questions
On a more practical note, you must be fluent with mathematical notation in order to score full credit on free response (FR) questions. Even if you know how to do a problem and get a correct final answer, if you cannot put those thoughts into complete mathematical sentences using proper calculus notation, then your score on the FR section will not be very high.
So let’s take some time to learn the language. ¡Vamos! Allons-y! Gehen wir! 가자!
The Zoo of Calculus Notation
Calculus notation builds upon the vast foundation of arithmetic and algebraic symbols. Everyone knows what the plus sign (+) means, but make sure that you also understand exponents, square (and higher) roots, and absolute value.
Perhaps most importantly, you must be comfortable working with variables and arbitrary constants (x, y, n, C, …). Any arithmetic operation that applies to numbers can apply equally well to variables, except that you shouldn’t expect a numerical result in that case.
Functions
Throughout the calculus textbook you have seen the notation f(x). This is the standard notation for a function.
A function is a rule that takes input (x) and does something to that input, resulting in an output (f(x) or y). What happens to the input is based entirely on how the function f was defined in the problem.
For example, suppose f(x) = x2 – 3x – 5. Can you find the value of f(4)? What about f(x + h)?
The idea is to plug in and simplify. Just be careful with your algebra!
f(4) = (4)2 – 3(4) – 5 = 16 – 12 – 5 = -1.
f(x + h) = (x + h)2 – 3(x + h) – 5 = x2 + 2xh + h2 – 3x – 3h – 5.
Limits
The limit of a function at a given point x = a measures how the outputs (y) might approach a fixed value L as the inputs (x) get closer and closer to the given point.
If the limit of f as x approaches a exists and equals some value L, then we write:
![]()
There are also one-sided limits and limits at plus or minus infinity.

For more about this concept, check out What is the Limit of a Function?.
Differential Calculus
There are various notations for the derivative of a function.
Suppose y = f(x) is a function. Then each of the following notation means exactly the same thing.
![]()
If we want to indicate that a number should be plugged into the derivative, then we write:
![]()
Higher derivatives also have their own set of notations.
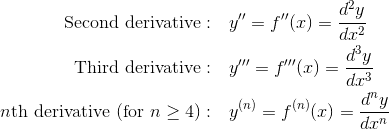
Check out Derivatives on the AP Calculus AB & BC Exams: A Refresher for more details.
Integral Calculus
When it comes to antiderivatives, definite and indefinite integrals, the various concepts can be very confusing at first. This is due in large part to the similarity of some of the notations.
Definite integrals have bounds (or limits of integration) indicated on the integral symbol, while indefinite integrals do not.
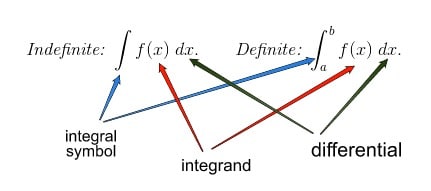
The indefinite integral stands for the most general antiderivative. In symbols we would write:
![]()
Here, the “answer” F is an antiderivative of f. Keep in mind, we tack on a “+ C” only when working out indefinite integrals. There should be no “C” in your answer to a definite integral.
Instead, you might use the Fundamental Theorem of Calculus to work out a definite integral.
![]()
See AP Calculus Exam Review: Integrals for more.
Sequences and Series
If you plan to take the AP Calculus BC exam rather than the AB, then you will also need to know about sequences and series.
Briefly, a sequence is nothing more than a list of numbers. Usually we study infinite sequences in calculus, which means that the list never actually stops.
Common notations for sequences are shown below.

On the other hand, a series the sum of a sequence. Typically we use sigma-notation to write the sum of a series.
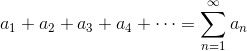
On the test you may find problems that ask you to prove a series converges or diverges. This is where your notational fluency is tested to its limits (no pun intended). Not only do you have to simplify complicated mathematical expressions involving sigma-notation, but you also have to write sophisticated logical arguments about those expressions!
Here is a helpful guide to help get you started: AP Calculus: Infinite Series
Summary
With enough practice, you can learn calculus notation and become fluent just as you might for any foreign language. Flip through a practice AP exam or three and if you see any symbols that you do not know, then study up on them. Ask your teacher; he or she has been around a long time and has seen it all (at least in terms of calculus).
In no time, you’ll move beyond being just a tourist in the land of mathematics and become a true speaker of the language!






Leave a Reply