The Fundamental Theorem of Calculus (FTC) is one of the most important mathematical discoveries in history. You might think I’m exaggerating, but the FTC ranks up there with the Pythagorean Theorem and the invention of the numeral 0 in its elegance and wide-ranging applicability. In this article I will explain what the Fundamental Theorem of Calculus is and show how it is used.
What is the Fundamental Theorem of Calculus?
Although the main ideas were floating around beforehand, it wasn’t until the 1600s that Newton and Leibniz independently formalized calculus — including the Fundamental Theorem of Calculus.

The FTC establishes a direct link between two different branches of mathematics: analysis and geometry. Analysis deals with properties of functions and rates of change, while geometry can be used to measure things about shapes.
Informally, the FTC states that the area under a curve y = f(x) (a geometric measurement) can be found using an antiderivative of the function (an analytic tool). This correspondence between area and antiderivatives is what makes the theorem so important and useful.
Statement of the Theorem (Definite Integral Form)
There are actually two different forms of the Fundamental Theorem of Calculus. Here is the one that is used most often.
If f is continuous on a closed interval [a, b], then
![]()
In the above formula, F is antiderivative for f. That is, F is a function whose derivative is equal to f. Using mathematical notation, we would say that F ‘(x) = f(x).
Using the FTC
The Fundamental Theorem of Calculus provides a powerful tool for evaluating definite integrals. Here are the steps:
- Find an antiderivative for the integrand, using appropriate integration formulas.
- Plug the upper limit (b) and lower limit (a) of integration into the antiderivative F.
- Subtract to find the final answer: F(b) – F(a).
Example
In the following example, we work out a definite integral using the FTC. Remember, cos x is the derivative of sin x. So sin x is the antiderivative of cos x.
![]()
Applications of the FTC
Any time a definite integral needs to be evaluated, the Fundamental Theorem of Calculus can come to the rescue. One of the most common applications you’ll see on the AP Calculus exams is area under a curve.
Area Under a Curve
If a function f(x) is nonnegative on an interval [a, b], then the area of the region under the curve can be computed by a definite integral. The limits of integration, a and b, specify the left and right boundaries of the region. The bottom boundary is the x-axis, and the top boundary is the graph of f(x) itself.
Let’s see how it works in one of the simplest cases, f(x) = x. The graph is a diagonal line through the origin.
Suppose b > 0. We will find the area under y = f(x) = x between x = 0 and x = b.
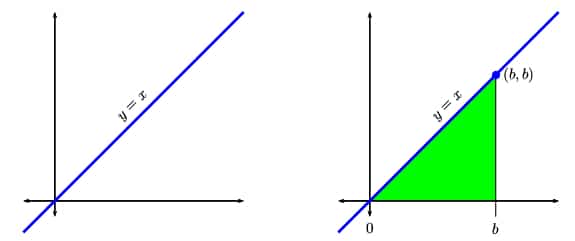
First set up the definite integral that computes the area. Then, according to the Fundamental Theorem of Calculus, we just need to find an antiderivative for f(x) = x. You can verify that F(x) = x2/2 does the trick.
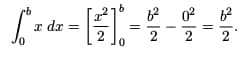
Areas and Antiderivatives
Now let’s try this same example (area under f(x) = x on [0, b]) but in a different way. By working the problem out using a different method, I hope to show you the remarkable connection between areas and antiderivatives.
Notice that the region under this particular function is simply a right triangle. You should know how to find the area of any triangle, using Area = (1/2)×(base)×(height). In this case, the base and height are the same: both are equal to b.
Therefore, by geometry we get Area = (1/2)×b×b = b2/2. The same result as we got above!
The fact that we get the same answer in this case might not be too surprising. However, the real power of the Fundamental Theorem of Calculus is that this link between areas and antiderivatives is true every single time. No matter how complicated the function is, you can find the area under the curve just using calculus.
The FTC and Accumulation Functions
There is a second part to the Fundamental Theorem of Calculus. It involves so-called accumulation functions. These are functions defined by a definite integral in which the upper limit of integration is the variable.
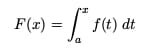
What is an Accumulation Function?
It’s helpful to think of an accumulation function as an “area so far” function. For any input x, the value of F(x) is the area under f from a to x. As x increases, more of the area gets “painted.”
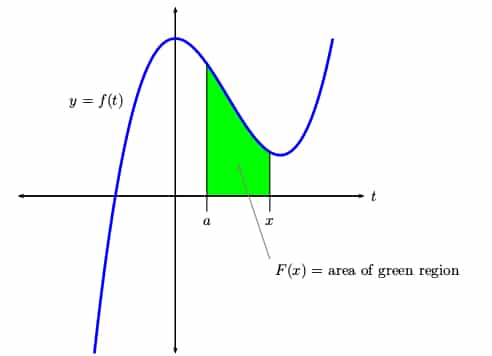
For example, the accumulation function for f(x) = x with left endpoint a = 0 is F(x) = x2/2. This is because the area under y = x on the interval [0, x] is equal to the area of the triangle with base and height both each to x.
The Second Fundamental Theorem of Calculus
The second part of the FTC states that the accumulation function is just a particular antiderivative of the original function. Equivalently, the derivative of an accumulation function for a function f is equal to f(x) itself.
Here’s the formal statement of the theorem.
If f is continuous on a closed interval [a, b], then
![]()
Using the Second Fundamental Theorem
On the AP Calculus exam, you may be asked to take the derivative of an accumulation function. The FTC is just the right tool for the job. These problems can range from very easy to much more challenging, so let’s see a couple easy examples first.
Example Problem 1
![]()
In this problem, the FTC can be applied directly. Notice how the variable t gets swapped out and becomes x.
![]()
Example Problem 2
![]()
This time, we need to reverse the order of integration first. Remember, this introduces a negative.
![]()
The Chain Rule and the FTC
In the above examples, we could use the theorem because one of the limits of integration happened to be a single variable x. What if one or both of the limits of integration are functions of x? This situation can be handled with a more general formula that involves the Chain Rule.
Suppose u and v are both differentiable functions of x. Then
![]()
Here’s how it works:
Example Problem 3
![]()
Solution:
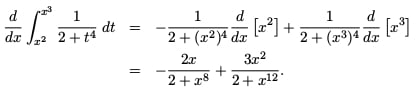
Final Thoughts
As with any topic on the AP Calculus exams, there is a lot to understand about the Fundamental Theorem of Calculus. However I hope that after having read this article, you have a much better understanding.





Leave a Reply