The process of elimination is a handy tool that can help give you the edge on the multiple choice sections of the AP Calculus AB or BC exam. In this article, we’ll see how the technique can be used effectively.

What is the Process of Elimination?
Suppose you’re working on a difficult multiple choice question. No matter what you try, you just can’t seem to crack this one. Or maybe there’s a method that you know would work but would be way too time-consuming.
You still might be able to increase your odds of getting a correct answer by process of elimination!
Without elimination, pure guessing gives you a correct answer in 1 out of every 4 questions, or 25% of the time. Once you start eliminating wrong answers, your odds go up.
| Number of answers eliminated | Chance of guessing correct |
|---|---|
| 0 | 25% |
| 1 | 33.3% |
| 2 | 50% |
| 3 | 100% |
We’ll talk about a few techniques for getting rid of wrong answers. Keep in mind though, this process works differently in mathematics than in other subjects like history, reading, or biology.
Getting Rid of Obviously Incorrect Answers
In high school history your teacher may have tried to lighten the mood on a test by including answers that could not possibly be correct. For example,
Where is Cairo located?
- A. Egypt
- B. Turkey
- C. Libya
- D. The Moon
Choice A is correct, and choices B and C are at least in the same general area. But choice D is clearly just a joke and should not be chosen, even as a guess.

Unfortunately, there will never be these kinds of joke answers on the AP Calculus exam.
Instead, what makes a mathematical answer “obviously” incorrect is often much more subtle.
Let’s look at two examples below.
Example 1 – Read the Problem Carefully
The function 4x3 – 8x2 + 1 on the interval [-1, 1] has an absolute minimum at x =
- A. -11
- B. -1
- C. 0
- D. 4/3
Suppose you have no idea how to find an absolute minimum. But notice that the question has two specific clues that allow you to eliminate two choices right away. The question asks for an x-value, and the given interval (of x-values) is [-1, 1]. Therefore, scratch both A. -11 and D. 4/3 off the list.
Now your probability jumps to 1 out of 2, or 50% for correctly guessing a correct answer.
(By the way, the correct answer is B. -1, however if you’re not careful you might incorrectly choose -11 because f(-1) = -11. We’ll discuss more about common student mistakes below.)
Example 2 – Know Your Theorems
If c satisfies the conclusion of the Mean Value Theorem for derivatives for f(x) = 2sin x on the interval [0, π], then c could be
- A. 0
- B. π/2
- C. π
- D. There is no value of c on [0, π]
I know it’s extremely tempting to choose D. However answer choice D is the first one that I would eliminate! Here’s why.
According to the Mean Value Theorem (MVT), as long as a function is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then there must be a value c satisfying the conclusion of the MVT.
We know that f(x) = 2sin x is continuous on all real numbers, so certainly the function is continuous on [0, π].
Furthermore, f ‘(x) = 2cos x exists for all real numbers.
So in particular, f is differentiable on (0, π).
Therefore, the conclusion of the MVT must be satisfied. Eliminate D, and now you if you had to guess, your chances stand at 33.3%
By the way, the correct answer turns out to be B. π/2. You might want to brush up on the MVT if you don’t know how to obtain that result.
Estimation
Estimation is a powerful technique that should be used whenever possible on the test. Not only can it help you to eliminate wrong answers, but it also aids in checking your work.
Here are a few examples to illustrate the point.
The sum of the infinite geometric series, 2 – 2/3 + 2/9 – 2/27 + . . . is
- A. -6
- B. -3
- C. 3/7
- D. 3/2
First note that the series alternates, that is, terms are alternately added and subtracted. Also note that the terms themselves keep getting smaller (closer to zero).
Starting with a value of 2, then 2/3 is taken away, so now the value is between 1 and 2. Because the rest of the terms alternate and contribute less and less to the sum, we can be sure that the answer will remain close to 2.
Already we can eliminate both negative answers, A and B.
In fact, we can even get rid of choice C, because we know that our sum must be between 1 and 2.
The answer must be D. 3/2.
Note, the “correct” way to solve this question is to use the Geometric Series Formula. Here, the first term is a = 2, and the common ratio is r = -1/3.
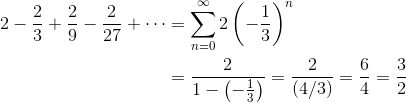
Avoid Common Mistakes
Another technique used by the test makers to create a challenging test is to include some answers that would result from the most common errors that student make.
Often, the error answer choices are too “simple” to be correct.
For example, consider the following question.
Find the derivative of f(x) = x2 (x – 2)7.
- A. 14x(x – 2)6
- B. (x – 2)6 (9x2 – 4x)
- C. (x – 2)6 (-5x2 – 4x)
- D. 7x2(x – 2)6
Now if you’re going too quickly, you might forget to use the Product Rule. If that’s the case, then you would mistakenly get: (2x)7(x – 2)6, which is equivalent to choice A.
But choice A is not right. If you know the product rule, then you know the answer can’t be so simple. Eliminate it!
Instead, using the product rule correctly, you should have come up with:
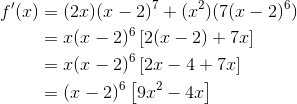
Choice B is correct.
In fact, in this example, you could have also eliminated D because it’s too simple to be the correct use of the product rule too. Then it would be down to B and C, a 50-50 shot if you had to guess from here.

Conclusion
The process of elimination can help you when you have to guess on multiple choice questions. Techniques that may be useful on the AP Calculus tests include:
- Eliminating obviously incorrect choices
- Estimating
- Watching out for common errors





Leave a Reply