Any given series either converges or diverges. But did you realize that there were different kinds of convergence? In this review article, we’ll take a look at the difference between absolute and conditional convergence. Along the way, we’ll see a few examples and discuss important special cases.
Absolute and Conditional Convergence
If a series has a finite sum, then the series converges. Otherwise, the series diverges.
However, we do make a distinction between series that converge very strongly, and those that only just barely converge. It all boils down to the signs of the terms.
- A series Σan converges absolutely if the series of the absolute values of its terms converges. That is, if Σ|an| also converges.
- A series Σan converges conditionally if the series converges but the associated series of absolute values Σ|an| diverges.
Classifying Series
It’s important to realize that both absolute and conditional convergence are still types of convergence. It’s not that a conditionally convergent series sometimes converges and sometimes not. Instead, we’re talking about the behavior of a related series: what happens when we get rid of all the negative signs in the series? If the new series of all positive terms also converges, then the original series converges in the strongest possible sense (absolute convergence).
So, there are only three possibilities:
- A series could converge absolutely.
- It could converge conditionally.
- Or, the series could diverge.

Prototypical Examples
Let’s talk about three basic series to help illustrate the point.
Usually the question of absolute versus conditional convergence pertains to series that have a mixture of positive and negative terms — as in an alternating series. (You can check out this review article for more details about alternating series: AP Calculus BC Review: Alternating Series.)
Example 1 — Absolutely Convergent
First, let’s consider the following series.
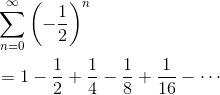
This series is both alternating (the signs switch back and forth) and geometric (there is a common ratio). In fact, because the common ratio, r = -1/2, has absolute value less than 1, we know that this series converges.
But is the convergence absolute or conditional?
Consider the related series of absolute values of each term:
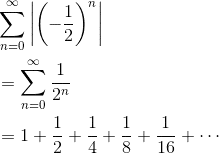
Again, we have a geometric series. But this time, the ratio is positive: r = 1/2. Still, |r| < 1, so the series of absolute values of terms converges as well.
Therefore, we have shown that the original series is absolutely convergent.
Caution: The two series (original vs. absolute values) are not usually going to converge to the same value. Indeed, using the formula for the sum of a geometric series, we can find out the sums explicitly:
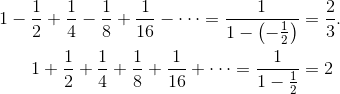
Example 2 — Conditionally Convergent
Next, consider the alternating harmonic series.
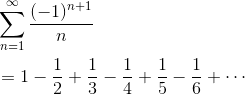
This series does converge. How can we tell? Use the Alternating Series Test.
The absolute value of the general term is equal to 1/n, which decreases and limits on the value 0 (as n → ∞). This implies that the original alternating series is convergent.
But how convergent is it really?
The series of absolute values is famous. It’s called the harmonic series, and we know that it diverges!
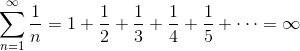
Therefore, by definition, the alternating harmonic series is conditionally convergent.
Example 3 — Divergent
Finally, let’s take a look at the series of powers of -1.
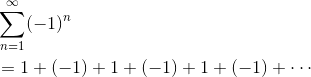
This series has no chance of converging at all because the limit of the general term is not zero. In fact, the limit of (-1)n as n → ∞ doesn’t exist at all!
Therefore, this series is divergent. There is no need to check the sum of absolute values at all.
The p-Series Test and Conditional Convergence
There is a very important class of series called the p-series.
By definition, a p-series is a series of the form:
![]()
There is an extremely simple test for convergence.
- If p > 1, then the series converges.
- If p ≤ 1, then the series diverges.
For example, the harmonic series, Σ1/n is a p-series with p = 1. According to the chart above, this series must diverge.
On the other hand, the series of reciprocals of squares, Σ1/n2 converges because it’s a p-series with p = 2, and 2 is greater than 1.
Alternating p-Series
But what about the alternating versions of the p-series?
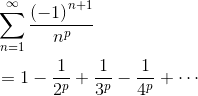
This time, the answer depends on the Alternating Series Test. As long as p > 0, then there will be a positive power of n in the denominator. So we would have 1/np → 0 as n → ∞, which in turn proves that the alternating series converges.
However, the convergence is only conditional if p ≤ 1 because of the p-Series Test. Absolute convergence is guaranteed when p > 1, because then the series of absolute values of terms would converge by the p-Series Test.
To summarize, the convergence properties of the alternating p-series are as follows.
- If p > 1, then the series converges absolutely.
- If 0 < p ≤ 1, then the series converges conditionally.
- If p ≤ 0, then the series diverges.
More About Absolute Convergence
There are two powerful convergence tests that can determine whether a series is absolutely convergent: the Ratio Test and Root Test. However, neither one can tell you about conditional convergence.
In fact, if the series is only conditionally convergent, then both the Ratio and Root Test will turn out to be inconclusive.
For example, let’s try the Ratio Test on the alternating harmonic series.
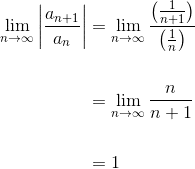
Because the limit is 1, the Ratio Test cannot determine whether the series converges or diverges.
You can find out more about these two tests here: AP Calculus BC Review: Ratio and Root Tests.





Leave a Reply