AP Calculus BC Review: Alternating Series

An alternating series is one in which the signs of the terms switch between positive and negative. These kinds of series show up fairly regularly in applications. So it’s important to know how to work with them.

In this review article, we’ll examine the properties of alternating series. We’ll also work through a number of examples similar to those you might find on the AP Calculus BC exam.

Sign, Sign, Everywhere a Sign

What makes a series alternating is the pattern of its signs. Positive terms alternate with negative terms forever. The first term may be either positive or negative.

So, if b₁, b₂, b₃, b₃, etc., are positive, then both of the following are alternating series.

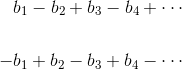
For example, the following series is alternating.

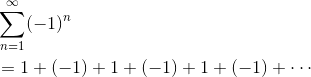
Here’s another example. Notice again how the factor of (-1)ⁿ switches the sign.

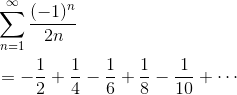
Here is one that is not easy to tell is alternating. In fact, it’s not obvious until you work out the value of each term. Remember your unit circle!

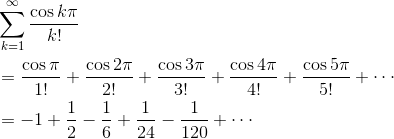
Alternating Series Test

There is actually a very simple test for convergence that applies to many of the series that you’ll encounter in practice.

Suppose that Σa_n is an alternating series, and let b_n = |a_n|. Then the series converges if both of the following conditions hold.

1. The sequence of (positive) terms b_n eventually decreases. That means that perhaps ignoring a few stray terms at the beginning, we have b_n > b_n+1 > b_n+2 > b_n+3 > …
2. The limit of the sequence (b_n) is equal to zero. That is,

   

Basically, if a series alternates, then as long as the terms get closer to zero, there must be a finite sum. Think of a bouncing ball. Each up bounce is a positive term, and each downward return is a negative term. If the next bounce is always smaller than the previous one, then eventually the ball will come to rest.

Error Bound

Directly related to the convergence test, there is an easy error estimate for these kinds of series.

If Σa_n is a convergent alternating series, then the nth partial sum, s_n, approximates the sum of the series to within an error bound of |a_n+1|.

Note that the error bound does not apply to divergent series.

Example — The Alternating Harmonic Series

The alternating harmonic series is the alternating sum of the reciprocals of all the natural numbers. That is,

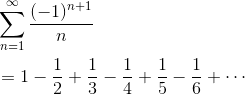
Does this series converge? Let’s use the Alternating Series Test to find out.

Here, b_n = |a_n| = 1/n, which decreases to 0 as n → ∞. Thus, the alternating harmonic sequence converges. (on the other hand, the plain old harmonic series, which consists of all positive fractions, actually diverges!)

How close is 1 – 1/2 + 1/3 – 1/4 + 1/5 to the value of the sum?

Just look for the next term, which would be -1/6. The error is only |-1/6| = 1/6 ≈ 0.16667.

Now, it can be determined through more advanced methods that the alternating harmonic sum is exactly ln(2), which is roughly 0.69315. Let’s verify our error bound estimate.

1 – 1/2 + 1/3 – 1/4 + 1/5 = 0.78333.

0.78333 – 0.69315 = 0.09018, which is well within the error bound estimate of 0.16667. It worked!

Examples from the AP Calculus BC Exam

Now that we’ve seen the theory, let’s apply what we know to a few example problems.

Determining Convergence

Determine which of the following series converge(s).

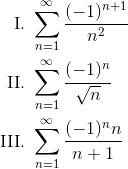
Solution

Each of the three series is alternating.

I. The absolute value of the general term is b_n = 1/n². Now, because 1/n² decreases to 0 as n → ∞, we know that the series converges by the Alternating Series Test.

II. This time, the absolute value of the general term is .

But still, the sequence of terms, b₁, b₂, b₃, b₃, etc., does decrease and limit onto 0. Again, the test tells us that this series converges.

III. Here, the general term is a bit trickier.

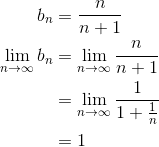
The limit is not equal to zero. In fact, that’s enough to conclude that the series must diverge. Remember that if the terms of any series do not limit on zero, then that series diverges.

You can check out AP Calculus BC Review: Series Convergence for more about series convergence and divergence.

Approximating π

In the seventeenth century, Gottfried Leibniz proved a remarkable series expansion for π.

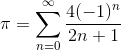
How many terms would be required to ensure that the partial sum of the series is within 1/100 of the actual value of π?

Solution

Let’s write out a few terms to see what kind of series this really is.

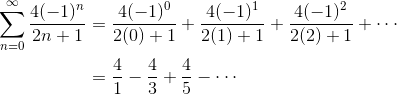
It seems like an alternating series, but how can we be sure? We can tell because of the (-1)ⁿ factor.

So this is a job for the alternating error bound estimate. In this example, we do not yet know how many terms should be in the partial sum, so we let that unknown number be n. Then we can solve for n using the goal: error < 0.01.

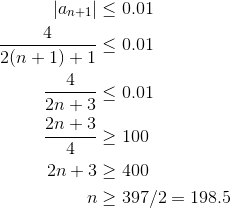
Therefore, since n must be a natural number, we need at least n = 199 terms to get the desired accuracy!

That may seem like a lot of work just to say that π ≈ 3.14, and I agree! Adding and subtracting almost two hundred fractions is not a very efficient approach for estimating π to within 0.01 accuracy. (Fortunately, there are better ways to find the digits of π in practice.)

However, this particular example does highlight the theoretic importance of alternating series and their properties.

Summary

• An alternating series is a series in which the signs of the terms alternate between positive and negative forever.
• The Alternating Series Test states that such a series will converge if the sequence of the absolute values of its terms decreases to zero in the limit.
• The error for the nth partial sum is bounded by |a_n+1|.