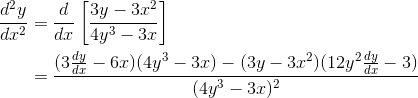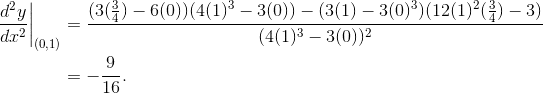There are only six free response problems on the AP Calculus exam, and yet we all dread these questions the most! But as long as you know your calculus, these problems are no more difficult than the multiple choice questions.
In this review, you’ll get an overview of the Free Response section and a few practice problems to work out. You can find the solutions by scrolling all the way down.
What to Expect on the Exam
The AP Calculus BC Exam consists of two main sections,
- Section I: Multiple Choice Questions (1 hour and 45 minutes, 45 questions)
- Section II: Free Response Questions (1 hour and 30 minutes, 6 questions)
Just like in the multiple choice section, the free response section is divided into two parts. Part A consists of two questions and requires the use of a (graphing) calculator. However, no calculator is allowed on Part B, which has four questions.
You are required you to write out all of your steps for each free response question, even if you used a calculator program or special feature to find the answer. Correct answers without supporting work may not receive credit.
Another major difference is that the free response questions usually consist of 2—4 subproblems. So while there are only 6 problems total, there may be closer to 20 problems if all parts are counted.
An important strategy to keep in mind: if you get stuck, move on! All of the problems are weighted equally and there is the possibility of earning partial credit.
Practice Problems
The following four problems are modeled after actual AP Calculus BC free response questions, two in each part. On the AP exam, there will be two more questions in Part B. For this practice set, give yourself 30 minutes for each part. Then, later on, you can go back and finish the parts that you didn’t get to for practice.
Free Response Section, Part A
Time — 30 minutes. A Graphing calculator is required for some problems or parts of problems.
-
- Let g(x) = x3 – 5x + 5.(a) Find the x– and y– coordinates of the relative maxima and relative minima.(b) Determine the equation of the tangent line to the graph at (-1, 9)
(c) Find the point(s) of inflection. Verify your answer.
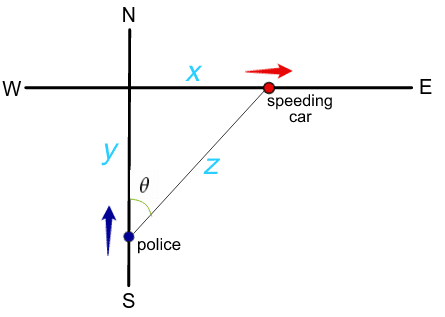
 Suppose a police officer is 1/2 mile south of an intersection, driving north towards the intersection at 25 mph. At the same time, another car is 1/2 mile east of the intersection, driving east (away from the intersection) at an unknown speed. The officer’s radar gun indicates 15 mph when pointed at the other car (that is, the straight-line distance between the officer and the other car is increasing at a rate of 15 mph).
Suppose a police officer is 1/2 mile south of an intersection, driving north towards the intersection at 25 mph. At the same time, another car is 1/2 mile east of the intersection, driving east (away from the intersection) at an unknown speed. The officer’s radar gun indicates 15 mph when pointed at the other car (that is, the straight-line distance between the officer and the other car is increasing at a rate of 15 mph).
(a) Find the speed of the other car in miles per hour.
(b) At what rate is the angle θ increasing in radians per second?
- Let g(x) = x3 – 5x + 5.(a) Find the x– and y– coordinates of the relative maxima and relative minima.(b) Determine the equation of the tangent line to the graph at (-1, 9)
Free Response Section, Part B
Time — 30 minutes. No calculator is allowed for these problems.
(Note, on the actual exam, this part consists of four question in 60 minutes.)
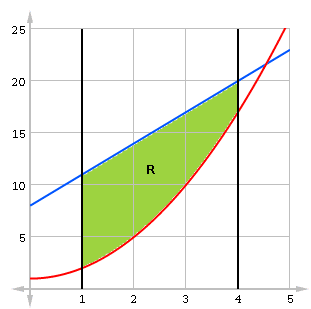
- Let R be the region enclosed by the graphs of y = x2 + 1 and y = 3x + 8, and the lines x = 1 and x = 4.(a) Find the area of R.(b) Set up, but do not integrate, an integral expression, in terms of a single variable, for the volume of the solid generated when R is revolved about the x-axis.
(c) Set up, but do not integrate, an integral expression, in terms of a single variable, for the volume of the solid generated when R is revolved about the line x = -2.
- Consider the equation x3 – 3xy + y4 = 1.(a) Write an expression for the slope of the curve at any point in terms of x and y.(b) Find the equations of the tangent lines to the curve at x = 1.
(c) Find the value of
 .
.
Solutions
The solutions below represent what might be acceptable work for a student to show in order to earn full credit. The purpose here is not to provide detailed explanations, but to demonstrate correct mathematical mastery. In fact, I’ve written a little bit more than a typical student might do on the exam so that you can follow my work easier.
Problem 1
-
- (a) g ‘(x) = 3x2 – 5.Set the derivative equal to 0 to find the critical numbers.

Use the second derivative test for relative extrema.
g ”(x) = 6x.
g ”(-1.291) = -7.746 < 0, so there is a relative maximum at this point.
g ”(1.291) = 7.746 > 0, so there is a relative minimum at this point.
Plug each critical number into the original function g to get the y-coordinates: g(-1.291) = 9.303, and g(1.291) = 0.697.
There is a relative minimum with coordinates (1.291, 0.697) and a relative maximum with coordinates (-1.291, 9.303).
(b) To get the slope of the tangent line at (-1, 9), evaluate g ‘(-1) = 3(-1)2 – 5 = -2.
Using point-slope form, y – 9 = -2(x – (-1)), or:
y = -2x + 7.
(c) Set the second derivative equal to 0 to find possible points of inflection.
g ”(x) = 6x = 0 → x = 0.
Since g ” < 0 for x < 0 and g ” > 0 for x > 0, there is a change in concavity at x = 0. This proves that there is an inflection point at x = 0.
Now g(0) = 5, so the inflection point is (0, 5).
- (a) g ‘(x) = 3x2 – 5.Set the derivative equal to 0 to find the critical numbers.
Problem 2
-
- (a) This is a related rates problem.
 By the Pythagorean theorem, x2 + y2 = z2.
By the Pythagorean theorem, x2 + y2 = z2.
Now taking derivatives with respect to time, we get:
 .
.Next, the given information tells us that dy/dt = -25, and dz/dt = 15. Furthermore, we know that x = 1/2 and y = 1/2. Therefore, by Pythagorean Theorem,

Now plug in to the related rate and solve for dx/dt:

Thus, the other car is going roughly 46.2 mph.
(b) This time, we use trigonometry:

The rate is in terms of radians per hour, so we must convert to radians per second by dividing by 3600.
Final answer: 0.01978 rad/sec.
- (a) This is a related rates problem.
Problem 3
-
- (a) Inspecting the graphs, y = 3x + 8 is always above y = x2 + 1 on the interval [1, 4].


The area is 45/2, or 22.5 square units.
(b) For a solid of revolution about the x-axis, it’s best to use the washer method.

(c) This time we have to revolve around a vertical line, x = -2. The most straightforward setup involves the shell method.
The radius of a typical shell is x – (-2) = x + 2.

- (a) Inspecting the graphs, y = 3x + 8 is always above y = x2 + 1 on the interval [1, 4].
Problem 4
- (a) The slope is equal to the derivative dy/dx. Use implicit differentiation to find the derivative.
 (b) First we plug in x = 1 into the original equation and then solve for the y-values.
(b) First we plug in x = 1 into the original equation and then solve for the y-values.
(1)3 – 3(1)y + y4 = 1
1 – 3y + y4 = 1
y(-3 + y3) = 0
So there are two points, y = 0 and y = ∛3.
At (1, 0), the slope is:

Now using point-slope form, we find the equation of the tangent line: y = x – 1.
At (1, ∛3), the slope is:

Again using point-slope form,

(c) Take the derivative of the derivative.

We have to plug in x = 0, y = 1. But we also need to know the value of dy/dx at (0, 1). So first compute:

Finally plug everything into the second derivative expression.


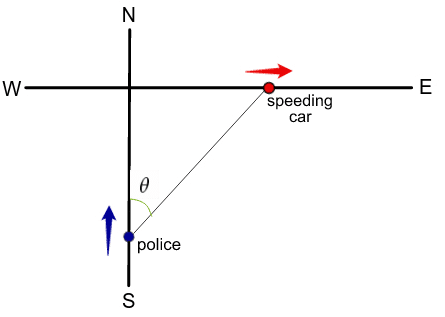 Suppose a police officer is 1/2 mile south of an intersection, driving north towards the intersection at 25 mph. At the same time, another car is 1/2 mile east of the intersection, driving east (away from the intersection) at an unknown speed. The officer’s radar gun indicates 15 mph when pointed at the other car (that is, the straight-line distance between the officer and the other car is increasing at a rate of 15 mph).
Suppose a police officer is 1/2 mile south of an intersection, driving north towards the intersection at 25 mph. At the same time, another car is 1/2 mile east of the intersection, driving east (away from the intersection) at an unknown speed. The officer’s radar gun indicates 15 mph when pointed at the other car (that is, the straight-line distance between the officer and the other car is increasing at a rate of 15 mph).
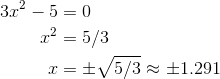
 By the Pythagorean theorem, x2 + y2 = z2.
By the Pythagorean theorem, x2 + y2 = z2.
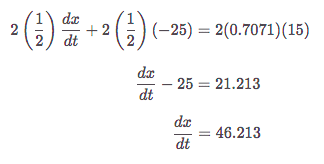
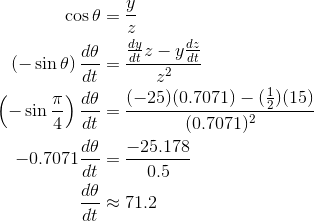
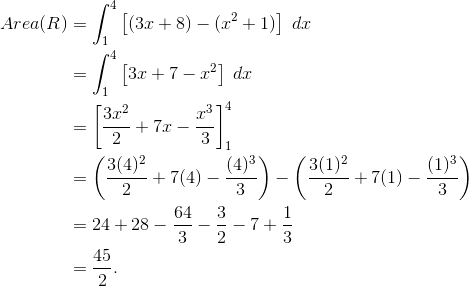
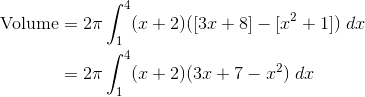
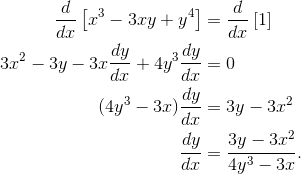 (b) First we plug in x = 1 into the original equation and then solve for the y-values.
(b) First we plug in x = 1 into the original equation and then solve for the y-values.