Slope fields show up on both the AP Calculus AB and BC tests. While at first this topic might seem daunting, the questions on the test are actually quite straightforward. Just keep one thing in mind: Go with the flow!

A slope field shows the direction of flow for solutions to a differential equation.
What is a Slope Field?
A slope field is a visual representation of a differential equation of the form dy/dx = f(x, y). At each sample point (x, y), there is a small line segment whose slope equals the value of f(x, y).
That is, each segment on the graph is a representation of the value of dy/dx. (Check out AP Calculus Review: Differential Equations for more about differential equations on the AP Calculus exams.)
Because each segment has slope equal to the derivative value, you can think of the segments as small pieces of tangent lines. Any curve that follows the flow suggested by the directions of the segments is a solution to the differential equation.
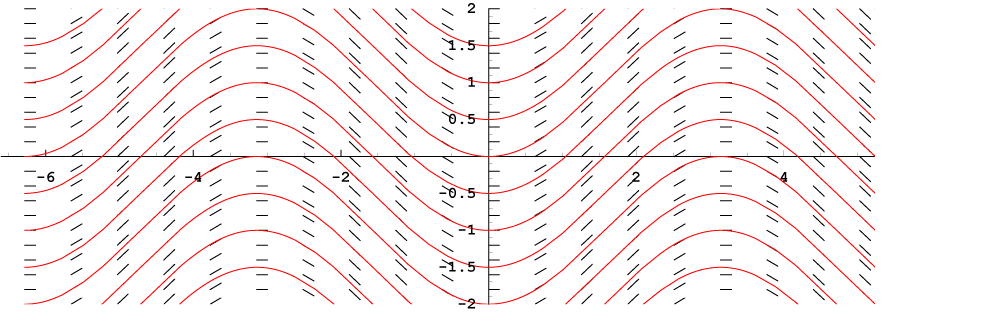 Each curve represents a particular solution to a differential equation.
Each curve represents a particular solution to a differential equation.
Example — Building a Slope Field
Consider the differential equation dy/dx = x – y. Let’s sketch a slope field for this equation. Although it takes some time to do it, the best way to understand what a slope field does is to construct one from scratch.
First of all, we need to decide on our sample points. For our purposes, I’m going to choose points within the window [-2, 2] × [-2, 2], and we’ll sample points in increments of 1. Just keep in mind that the window could be anything, and increments are generally smaller than 1 in practice.
Now plug in each sample point (x, y) into the (multivariable) function x – y. We will keep track of the work in a table.
| x – y | x = -2 | x = -1 | x = 0 | x = 1 | x = 2 |
|---|---|---|---|---|---|
| y = 2 | -2 – 2 = -4 | -1 – 2 = -3 | 0 – 2 = -2 | 1 – 2 = -1 | 2 – 2 = 0 |
| y = 1 | -2 – 1 = -3 | -1 – 1 = -2 | 0 – 1 = -1 | 1 – 1 = 0 | 2 – 1 = 1 |
| y = 0 | -2 – 0 = -2 | -1 – 0 = -1 | 0 – 0 = 0 | 1 – 0 = 1 | 2 – 0 = 2 |
| y = -1 | -2 – (-1) = -1 | -1 – (-1) = 0 | 0 – (-1) = 1 | 1 – (-1) = 2 | 2 – (-1) = 3 |
| y = -2 | -2 – (-2) = 0 | -1 – (-2) = 1 | 0 – (-2) = 2 | 1 – (-2) = 3 | 2 – (-2) = 4 |
Ok, now let’s draw the slope field. Remember, the values in the table above represent slopes — positive slopes mean go up; negative ones mean go down; and zero slopes are horizontal.
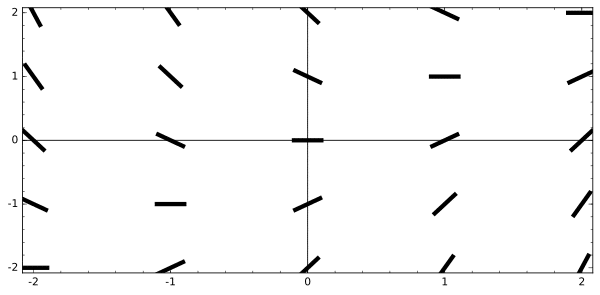
Spend some time matching each slope value from the table with its respective segment on the graph.
It’s important to realize that this is just a sketch. A more accurate picture would result from sampling many more points. For example, here is a slope field for dy/dx = x – y generated by a computer algebra system. The viewing window is the same, but now there are 400 sample points (rather than the paltry 25 samples in the first graph).
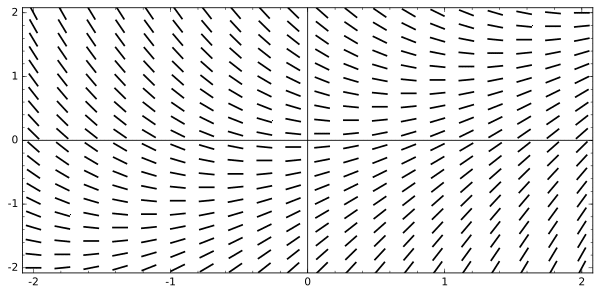 Slope field for dy/dx = x – y
Slope field for dy/dx = x – y
Analyzing Slope Fields
Now let’s get down to the heart of the matter. What do I need to know about slope fields on the AP Calculus AB or BC exams?
You’ll need to master these basic skills:
- Given a slope field, select the differential equation that best matches it.
- Given a slope field, estimate values of a solution with given initial condition.
- Sketch a slope field on indicated sample points, from a given differential equation.
We’ve already seen above how to sketch a slope field, so let’s get some practice with the first two skills in the list instead.
Sample Problem 1
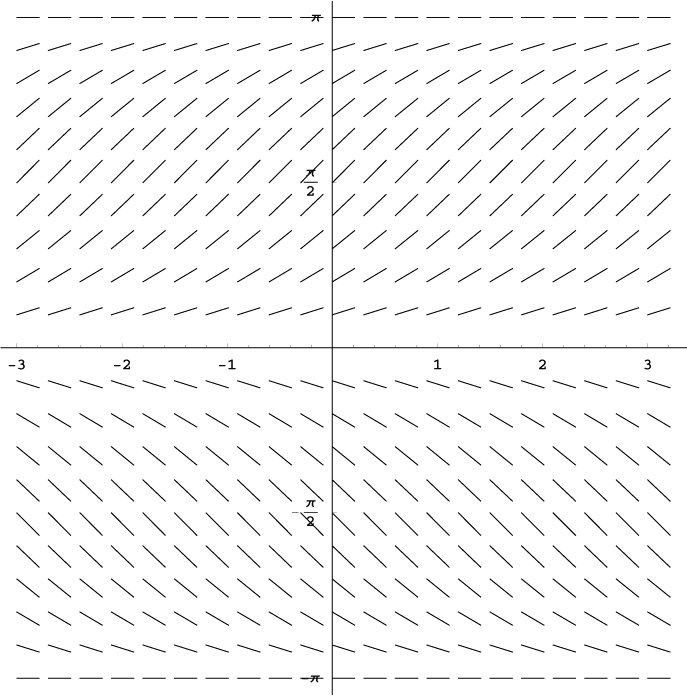
The slope field shown above corresponds to which of the following differential equations.
A. dy/dx = y2
B. dy/dx = sin y
C. dy/dx = -sin y
D. dy/dx = sin x
Solution
Look for the clues. The segments have the same slopes in any given row (left to right across the graph). Therefore, since the slopes do not change with respect to x, we can assume that dy/dx is a function of y alone. That eliminates choice D.
The horizontal segments occur when y = 0, π, and -π. However, the only point at which y2 equals 0 is y = 0 (not π or -π). That narrows it down to a choice between B and C.
Finally, notice that slopes are positive when 0 < y < π and negative when -π < y < 0. This pattern corresponds to the values of sin y. (The signs are opposite for -sin y, ruling out choice C).
The correct choice is B.
Sample Problem 2
Suppose y = f(x) is a particular solution to the differential equation dy/dx = x – y such that f(0) = 0. Use the slope field shown earlier to estimate the value of f(2).
A. -2.5
B. -1.3
C. 0.2
D. 1.1
Solution
Because f(0) = 0, the solution curve must begin at (0, 0). Then sketch the curve carefully following the directions of the segments. It helps to imagine that the segments are showing the currents in a river. Your solution should be like a raft carried along by the currents.
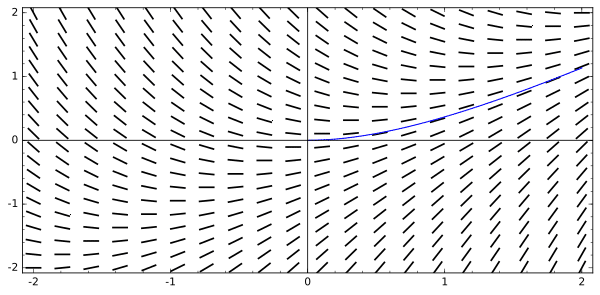
Then find the approximate value of f(2) on your solution curve.
The best choice from among the answers is: D. 1.1.
Slope Fields and Euler’s Method
Often if you see a slope field problem in the Free Response section of the exam, one part of the problem might be to use Euler’s Method to estimate a value of a solution curve.
While the slope field itself can be used to estimate solutions, Euler’s Method is much more precise and does not rely on the visual representation. Check out this review article for practice using the method: AP Calculus BC Review: Euler’s Method.
Summary
- Slope fields are visual representations of differential equations of the form dy/dx = f(x, y).
- At each sample point of a slope field, there is a segment having slope equal to the value of dy/dx.
- Any curve that follows the flow suggested by the directions of the segments is a solution to the differential equation.





Leave a Reply