In my experience, students often hit a roadblock when they see the word asymptote. What is an asymptote anyway? How do you find them? Is this going to be on the test??? (The answer to the last question is yes. Asymptotes definitely show up on the AP Calculus exams).
Of the three varieties of asymptote — horizontal, vertical, and oblique — perhaps the oblique asymptotes are the most mysterious. In this article we define oblique asymptotes and show how to find them.
What is an Oblique Asymptote?
An oblique (or slant) asymptote is a slanted line that the function approaches as x approaches ∞ (infinity) or -∞ (minus infinity). Let’s explore this definition a little more, shall we?
It’s All About the Line
Since all non-vertical lines can be written in the form y = mx + b for some constants m and b, we say that a function f(x) has an oblique asymptote y = mx + b if the values (the y-coordinates) of f(x) get closer and closer to the values of mx + b as you trace the curve to the right (x → ∞) or to the left (x → -∞), in other words, if there is a good approximation,
f(x) ≈ mx + b,
when x gets extremely large in the positive or negative sense.
Still with me? I understand completely if you’re still a little lost, but let’s see if we can clear up some confusion using the graph shown below.

As you can see, the function (shown in blue) seems to get closer to the dashed line. Therefore, the oblique asymptote for this function is y = ½ x – 1.
Finding Oblique Aymptotes
A function can have at most two oblique asymptotes, but only certain kinds of functions are expected to have an oblique asymptote at all. For instance, polynomials of degree 2 or higher do not have asymptotes of any kind. (Remember, the degree of a polynomial is the highest exponent on any term. For example, 10x3 – 3x4 + 3x – 12 has degree 4.)
As a quick application of this rule, you can say for sure without any work that there are no oblique asymptotes for the quadratic function f(x) = x2 + 3x – 10, because it’s a polynomial of degree 2.
On the other hand, some kinds of rational functions do have oblique asymptotes.
Rational Functions
A rational function has the form of a fraction, f(x) = p(x) / q(x), in which both p(x) and q(x) are polynomials. If the degree of the numerator (top) is exactly one greater than the degree of the denominator (bottom), then f(x) will have an oblique asymptote.
So there are no oblique asymptotes for the rational function, 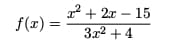 .
.
But a rational function like ![]() does have one. Knowing when there is a horizontal asymptote is just half the battle. Now how do we find it? This next step involves polynomial division.
does have one. Knowing when there is a horizontal asymptote is just half the battle. Now how do we find it? This next step involves polynomial division.
Polynomial Division to Find Oblique Asymptotes
If you’ve made it this far, you probably have seen long division of polynomials, or synthetic division, but if you are rusty on the technique, then check out this video or this article.
The idea is that when you do polynomial division on a rational function that has one higher degree on top than on the bottom, the result always has the form mx + b + remainder term. Then the oblique asymptote is the linear part, y = mx + b. We don’t need to worry about the remainder term at all.
Example Using Polynomial Division
Let’s see how the technique can be used to find the oblique asymptote of ![]() .
.
The long division is shown below.
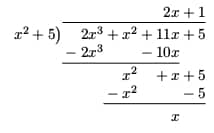
Because the quotient is 2x + 1, the rational function has an oblique asymptote:
y = 2x + 1.
Hyperbolas
Another place where oblique asymptotes show up is in the graphs of hyperbolas. Remember, in the simplest case, a hyperbola is characterized by the standard equation,
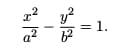
The hyperbola graph corresponding to this equation has exactly two oblique asymptotes,
![]()
The two asymptotes cross each other like a big X.
Example Involving a Hyperbola
Let’s find the oblique asymptotes for the hyperbola with equation x2/9 – y2/4 = 1.
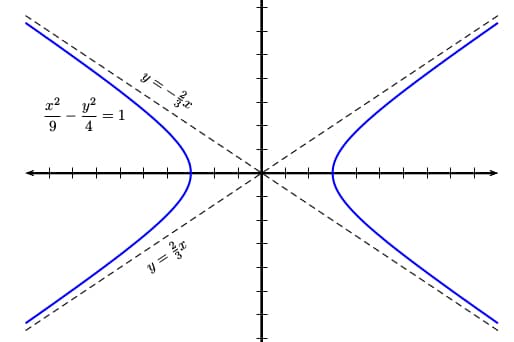
In the given equation, we have a2 = 9, so a = 3, and b2 = 4, so b = 2. This means that the two oblique asymptotes must be at y = ±(b/a)x = ±(2/3)x.
More General Hyperbolas
It’s important to realize that hyperbolas come in more than one flavor. If the hyperbola has its terms switched, so that the “y” term is positive and “x” term is negative, then the asymptotes take a slightly different form. Furthermore, if the center of the hyperbola is at a different point than the origin, (h, k), then that affects the asymptotes as well. Below is a summary of the various possibilities.

Final Thoughts
So when you see a question on the AP Calculus AB exam asking about oblique asymptotes, don’t forget:
- If the function is rational, and if the degree on the top is one more than the degree on the bottom: Use polynomial division.
- If the graph is a hyperbola with equation x2/a2 – y2/b2 = 1, then your asymptotes will be y = ±(b/a)x. Other kinds of hyperbolas also have standard formulas defining their asymptotes.
Keeping these techniques in mind, oblique asymptotes will start to seem much less mysterious on the AP exam!




Leave a Reply