Does a linear function have any asymptotes? Surprisingly, this question does not have a simple answer. However, I hope to show you that while linear functions do not have any vertical asymptotes, they will have either a horizontal or oblique asymptote, depending on the slope of the line.
What do the Experts Say?
Textbooks are silent on this question. No linear functions ever show up in asymptote examples or exercises. An internet search will turn up various arguments for as well as against the idea that a linear function might have an asymptote. What’s so strange about those simple linear functions that make even the experts disagree about their asymptotes?
In this article, I’ll explain (1) how a linear function may or may not have an asymptote, (2) the mathematical evidence supporting my claims, and (3) the reasons why some people say linear functions never have asymptotes. Along the way, we’ll briefly review the concepts linear function and asymptote.
What is a Linear Function?
A linear function is any function of the form f(x) = mx + b, where m and b are constants. Sometimes a linear function might be written in other forms, but as long as it can be simplified to the form mx + b (called slope-intercept form), it’s linear. The graph of a linear function is always a line.
Slope and y-Intercept
The constant m in the slope-intercept form is called the slope of the line. Slope describes how “tilted” the line is. When m is positive, the line is tilted upward (increasing from left to right). Conversely, when m is negative, the line tilts downward (decreasing from left to right). Lines with no tilt — horizontal lines — have zero slope (m = 0). In that case, we can write the line in a simpler way, as a constant function: y = b.
The other constant in the slope-intercept form, b, is the y-intercept, and it simply tells where the line intersects with the y-axis. For this discussion, we will be more interested in the slope (m) than the y-intercept.
Examples of Linear Functions and Graphs
Below are a few linear functions along with their graphs. The red line has positive slope (m = 1/2). The green one has negative slope (m = -3). The blue one is horizontal (m = 0).
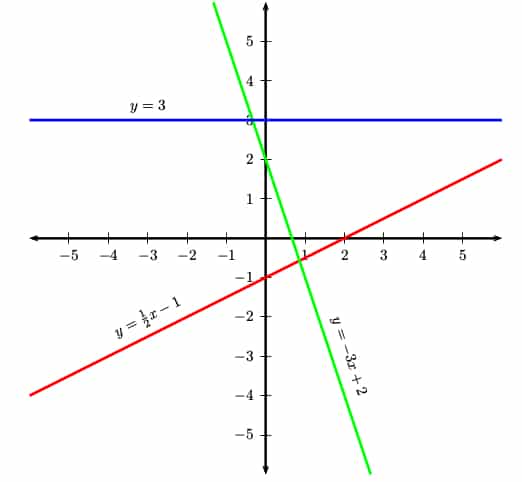
What is an Asymptote?
There are three types of asymptote: vertical, horizontal, and oblique (or slant). Each type is defined in a slightly different way, using limits.
We shall see that the slope is the most important factor in determining the asymptote of a linear function.
Vertical Asymptotes
A function f(x) has a vertical asymptote at x = k if any of the following limit statements are true:
![]()
This can only happen if the function has a discontinuity, or “break,” at x = k. For example, there are two vertical asymptotes in the function graphed below:

Since a linear function is continuous everywhere, linear functions do not have any vertical asymptotes.
Horizontal Asymptotes
By definition, a function f(x) has a horizontal asymptote at y = k if either of the two limit statements are true:
![]()
Below is a function (not linear) that has two horizontal asymptotes.
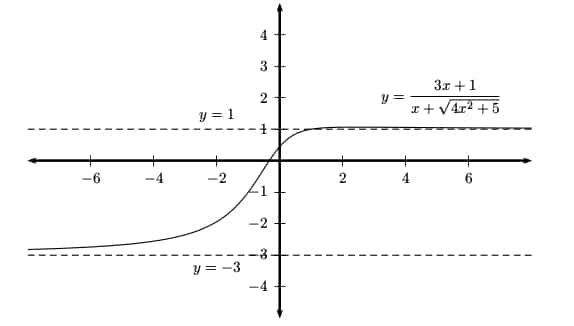
The only way that a linear function, f(x) = mx + b, could have a finite limit as x approaches infinity is if the slope is zero. That is, f(x) must be a constant function, f(x) = b.
Therefore, when m = 0, the linear function has a horizontal asymptote at y = b. Notice, that’s the same exact function you started with (f(x) = b). In other words, the linear function is its own horizontal asymptote!
Oblique Asymptotes
A horizontal asymptote is a slanted line to which the values of the function approach as x approaches infinity or minus infinity. Typically we look for oblique asymptotes in rational functions (functions that have the form of a fraction, f(x) = p(x) / q(x), in which both p(x) and q(x) are polynomials) where the degree of the numerator is one more than the degree of the denominator, or in special kinds of graphs such as hyperbolas (as pictured below).
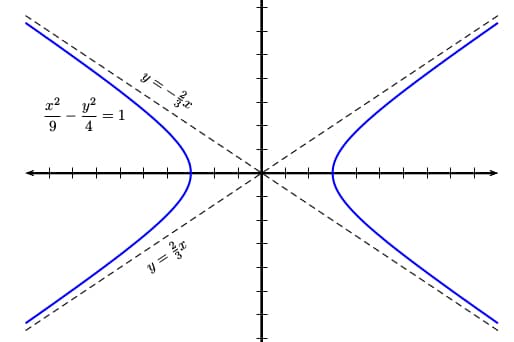
Although a linear function f(x) = mx + b does not seem to fit any of these categories, it actually does count as a rational function (similar to how we consider a square to be a special kind of rectangle).
But what are the numerator and denominator in a linear function? Remember that any number n can be turned into a fraction by writing it over a denominator of 1. That is, n = n/1. In a similar way, mx + b = (mx + b)/1 is a rational function. Following the usual procedure for finding the oblique asymptote of a rational function (polynomial division), we get y = mx + b as the asymptote. This time, as long as m ≠ 0, the function has an oblique asymptote. As before, the asymptote happens to be the same as the original linear function!
Linear Functions and Asymptotes — What’s the Problem?
A typical problem on the AP Calculus exam involving asymptotes might ask you to find the vertical, horizontal, and/or oblique asymptotes of a rational function. The methods for finding asymptotes of rational functions all rely on the fractional form of the function.
Some might say that linear functions do not have asymptotes because “there is no denominator.” However, many other kinds of functions have asymptotes, too, so it’s not just about the fractional form. Besides, as mentioned above, there is a denominator — it’s just 1.
Still Not Convinced?
Others might say that because functions must approach their asymptotes (not land exactly on top of them), then that disqualifies the linear functions from being their own asymptotes. While this argument might be convincing for the vertical asymptotes (remember, linear functions can’t have any of those), there is nothing in the definition of horizontal or oblique asymptote that prevents a graph from intersecting its own asymptote once, twice, or even infinitely many times.
Call it a technicality if you want, but there’s no rule saying a function can’t be the same as its asymptote.
Conclusion
In a way, asking whether a linear function has an asymptote is simply a non-question. This is because a linear function is, by definition, the graph of a line, and asymptotes are lines that show the end behavior of the function. So we can say that a linear function is its own asymptote. Fortunately, you will never be asked to find the asymptotes of a linear function on the AP Calculus exams. On the other hand, it is fun and helpful to think about how the mathematical definition of asymptote applies even in this strange situation.



Leave a Reply