AP Calculus Review: Exponential Functions

Exponential functions play a key role in a wide array of applications including population growth. These important functions show up on both the AP Calculus AB and BC exams. So here’s what you should know about them for the test.

Exponential Functions — Definitions

An exponential function is one that involves a constant positive base to a variable exponent. The most basic exponential is: f(x) = a^x, where a > 0 is a constant.

Other variations include coefficients that scale the graph horizontally or vertically. Adding or subtracting a constant shifts the graph up or down.

Furthermore, there is a certain constant called e (Euler’s constant) that is so useful as a base that we call e^x the natural exponential function.

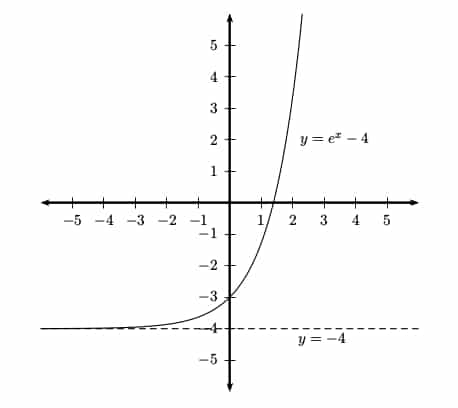
Facts and Properties

The exponential function f(x) = a^x satisfies the following properties.

• The domain is all real numbers, (-∞, ∞).
• The range is all positive real numbers, (0, ∞).
• The y-intercept is (0, 1), but there is no x-intercept.
• If a > 1, then f increases on its domain.
• If 0 < a < 1, then f decreases on its domain.
• The graph is concave up on its entire domain.
• The line y = 0 is a horizontal asymptote.

Differentiating Exponential Functions

The natural exponential has the remarkable property that it is its own derivative. That property alone is what makes the function e^x so essential to almost all branches of science.

When the base is something other than e, then the derivative formula involves a multiple of the natural logarithm of the base.

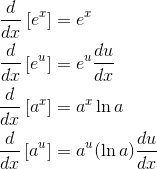
Check out the following article for more details about logarithms and exponent properties: AP Calculus Review: Properties of Exponents and Logarithms.

Example 1

Find the absolute minimum and maximum values of

Solution

The function g(x) is technically not an exponential function, however it does involve an exponential.

Let’s take the first derivative. Don’t forget product rule!

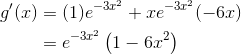
Find the critical numbers by setting g ' equal to 0 and solving. Note that because the exponential function itself can never be 0, the only factor that matters here is 1 – 6x².

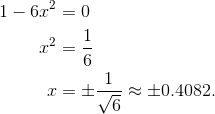
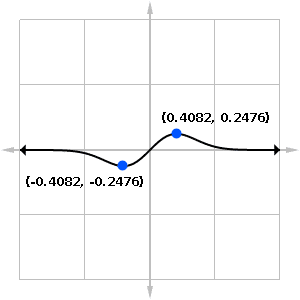
Finally, plug the two critical numbers into the original function to determine minimum and maximum. A sketch of the graph also helps to prove that the absolute min and max do occur at those points.

• g(-0.4082) = -0.2476 (minimum value)
• g(0.4082) = 0.2476 (maximum value)

Integrating Exponential Functions

Because the derivative of e^x is equal to e^x, you can expect its antiderivative to be the exact same thing. (But don’t forget the “+ C“!)

Example 2

Let . Find the value of c guaranteed by the Mean Value Theorem for Integrals so that f(c) is equal to the average value of f on the interval [1, 3].

Solution

We must first find the average value of the function on the given interval. This is a job for an integral. Note that there will be a substitution: u = 2x.

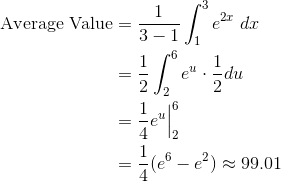
Next, set f(c) = 99.01 and solve for c.

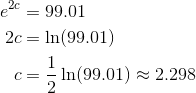
Related Topics

The exponential also shows up in a number of applications on the AP Calculus exams.

Exponential Growth Models

Any situation in which the rate of growth is proportional to the amount present lends itself directly to an exponential model.

The differential equation y ' = ky, where k is a constant, has the general solution, y = Ae^kx. Here, the value of the constant A is equal to the initial population, y(0).

Example 3

A certain bacteria culture has 1000 cells initially.

The amount X, in grams, of a radioactive isotope decays according to the equation dX/dt = -0.03X, where time t is measured in days. Determine the half-life of the isotope to the nearest day. (Note: the half-life of a substance is the amount of time it takes for exactly one-half of the substance to decay.)

Solution

First, we can build the exponential model (Ae^kx) based on the given information. Here, the initial amount is A = 1000, and the decay constant is k = -0.03. So, the appropriate exponential model would be:

Next, to find the half-life, we set X(t) = 500 (because that’s half of 1000), and solve for t.

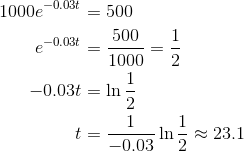
Thus the half-life is about 21 days.

The Logistics Growth Model

the logistics growth model is an equation the models population growth up to a constant carrying capacity M.

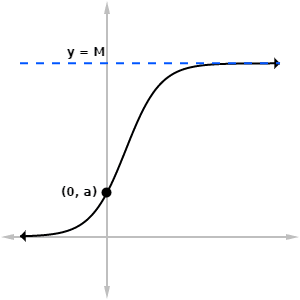
The natural exponential e^x makes an appearance as part of the solution to the logistics differential equation.

For more information and examples, check out: AP Calculus BC Review: Logistics Growth Model.

The Maclaurin Series for e^x

Taylor and Maclaurin series only show up on the AP Calculus BC exam. You should probably memorize the Maclaurin series for the natural exponential function.

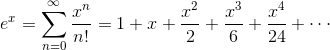
Example 4

Find a power series expansion for .

Solution

We just have to work with the Maclaurin series for the natural exponential. I’ve color coded certain parts to make it a little easier to follow.

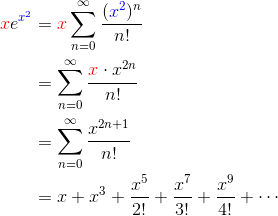
Summary

• Exponential functions have the basic form f(x) = a^x, where a > 0 is a constant. But the graph can be scaled or shifted by including appropriate coefficients and constant terms.
• The derivative of e^x is equal to e^x. The derivative of a^x is a^x ln a.
• The antiderivative (integral) of e^x is equal to e^x + C. The antiderivative of a^x is a^x / (ln a) + C.
• The general solution of the differential equation y ' = ky is the exponential function, y = Ae^kx.
• The solution to the logistics growth model equation also involves exponentials.
• The Maclaurin series (power series) of the natural exponential function is: