It’s important to know the basics. You have to have a solid foundation in order to build a skyscraper, right? In this short review, I’ll discuss the basic formulas and properties that you’ll need to master in order to success on the AP Calculus exam.

The Basic Formulas
First and foremost, you must be you must know arithmetic, algebra, and trigonometry inside-out. For a quick review check out the following helpful articles.
Once you have mastered those fundamental topics of mathematics, you can then build your expertise in calculus.
Calculus-Specific Formulas
There are a number of basic formulas from calculus that you need to memorize for the exam.
Moreover, if you plan to take the Calculus BC exam, then you will have to know every formula that could show up on the AB exam, plus a whole slew of additional formulas and concepts that are specific to the BC exam.
It might help to look through the following “Cram Sheets” first.
The formulas can be categorized into four Big Ideas.
- Limits and Continuity (AB and BC)
- Derivatives and Their Applications (AB and BC)
- Integrals and Their Applications (AB and BC)
- Sequences and Series (BC only)
Limits and Continuity
There are not a lot of formulas for computing limits. Instead, each limit problem may require different algebraic or trigonometric “tricks.” However, it helps to know L’Hospital’s Rule:
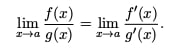
A function f is continuous at a point x = a if:
![]()
The Intermediate Value Theorem (IVT) states that if a function f is continuous on a closed interval [a, b], and if L is any number between f(a) and f(b), then there must be a value x = c where a < c < b, such that f(c) = L.
Average Rate/Velocity
Although this formula does not have to do with limits directly, it’s a useful concept and very important for developing the concepts of derivatives.
![]()
Derivatives and Their Applications
Limit definition for the derivative:
![]()
Make sure you know every derivative rule.
Basic Differentiation Rules
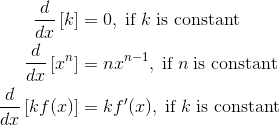
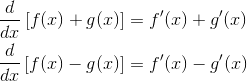
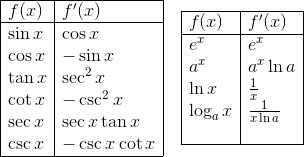
Product and Quotient Rule
![]()
![]()
Chain Rule
![]()
Inverse Functions
![]()

Polar and Parametric Functions
The AP Calculus BC exam also includes polar and parametric functions and their derivatives.
The derivative of a polar function, r = f(θ):
![]()
The derivative of a parametric function, x = f(t) and y = g(t):
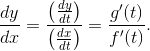
Applications of Derivatives — Velocity
It’s important to know the relationship between position, velocity, and acceleration in terms of derivatives.
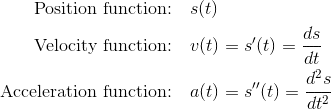
On the AP Calculus BC test, the position may be a vector function.
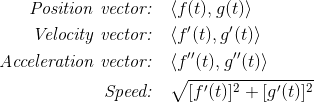
Mean Value Theorem and Rolle’s Theorem
There are two related theorems involving differentiable functions, the Mean Value Theorem, and Rolle’s Theorem.
Mean Value Theorem (MVT): Suppose f is a function that is continuous on [a, b] and differentiable on (a, b). Then there is at least one value x = c, where a < c < b, such that
![]()
Rolle’s Theorem: Suppose f is a function that is continuous on [a, b], differentiable on (a, b), and f(a) = f(b). Then there is at least one value x = c, where a < c < b, such that f '(c) = 0.
Integrals and Their Applications
![]()
![]()
![]()
![]()
![]()

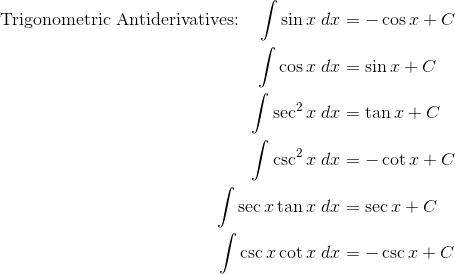
On the BC test, you may have to find velocity and speed for a vector position function.
Integration Techniques
The following formulas are useful for working out integrals of more complicated functions. Think of each rule as a potential tool in your toolbox. Sometimes an integral will require multiple tools.
- u-Substitution

- Integration By Parts (BC only)

The Fundamental Theorem of Calculus (FTC)
The Fundamental Theorem of Calculus comes in two versions.
![]()
If F(x) is any particular antiderivative for f(x), then
![]()
Average Value and Mean Value Theorem for Integrals
![]()
Mean Value Theorem for Integrals (MVTI): Suppose f is continuous on [a, b]. Then there is at least one value x = c, where a < c < b, such that
![]()
Applications of Integrals
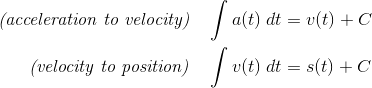
![]()
On the AP Calculus BC exam, you may also have to find the length of a parametric curve defined by x = f(t) and y = g(t).
![]()
Use the washer or shell method to find the volume of a solid of revolution.
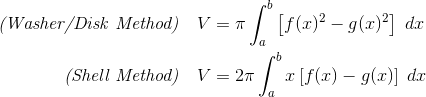
Sequences and Series
One of the most important formulas involving series is the Geometric Series Formula:
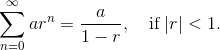
Convergence Tests
Given a series,
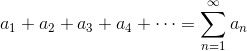 ,
,
the following tests can help to prove that the series converges or diverges.
- p-series test. If the series has general term an = 1/np, then the series converges if p > 1 and diverges if p ≤ 1.
- Alternating series test. If the series is alternating (i.e., the terms alternate in sign forever), then the series converges if and only if an → 0 as n → ∞. And in that case, the error bound for the nth partial sum is |an+1|.
- Ratio test.

However, if the limit is > 1, then the series diverges. No information if the limit equals 1. - Root test.

Just as in the ratio test, if the limit is > 1, then the series diverges. No information if the limit equals 1.
Taylor and Maclaurin Series
If a function f is differentiable to all orders, then you can build its Taylor series centered at c as follows.
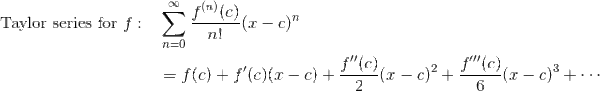
A Taylor series centered at c = 0 is called a Maclaurin series. Below are some common Maclaurin series that are worth memorizing.
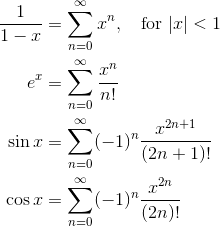
Get Ready!
This list provides just the foundation for your study. Memorizing a list of formulas will not guarantee you a high score on the exam. You must also understand how and when to use each formula.
Furthermore, there are tons of more specialized formulas that didn’t make it to this list. Master all of the AP topics and practice, practice, practice!






Leave a Reply