Limits and continuity are topics that show up frequently on both the AP Calculus AB and BC exams. In this article, we’ll discuss a few different techniques for finding limits. We’ll also see the “three-part” definition for continuity and how to use it.
Keep in mind this is just a short review. Much more can be said about limits and continuity in general.
Limits
What is a limit anyway? In simple terms, a limit for a function is a particular y-value that the function approaches as x is allowed to approach a specified value. We use the following notations for a limit:
![]()
This notation means: “The y-value of f(x) approaches L as x approaches a.
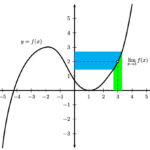
It’s important to realize that the limit value does not depend on the actual value of f(a). For example, in the graph below, the limit exists at x = 3 even though the function has a hole in the graph at that point.
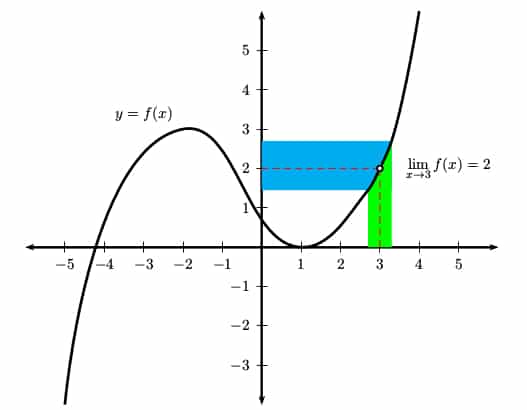
Finding Limits Algebraically
When graphs are not given, it can be tricky to find limits. Usually, you have to simplify the expression in some way and then plug in the x-value. Common techniques include:
- Factor and cancel
- Combine fractions / LCD
- Rationalize a radical
- L’Hospital’s rule
Let’s see how these techniques might be used in the following examples.
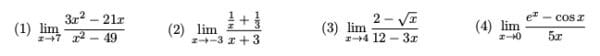
-
Factoring Example
Problem 1 is a typical case in which factoring helps out. If the numerator and denominator are both polynomials, then try factoring first. Once the common factor is canceled, then you can plug in the x value to find the limit.

-
Fractions and Least Common Denominator
Because problem 2 has fractions on top of fractions, we look for ways to simplify or “get rid” of some of the fractions. In my experience, the easiest way to do this is by finding the least common denominator (LCD). Find the denominators of the small fractions, x and 3 in this case. Then the LCD would be 3x. Multiplying the LCD to both the top and bottom allows you to simplify the expression.

-
Rationalizing Radicals
In algebra, rationalizing means changing the form of a number to avoid radicals in the denominator. The situation is different in calculus. Sometimes the radical is in the numerator, and we rationalize the expression anyway. The reason for this is that rationalization often changes the form in just the right way so that the limit problem can be solved.
To rationalize an expression, multiply both the numerator and denominator by the conjugate.
The conjugate of a radical expression is found by changing the sign in front of the radical. In other words, the conjugate of (a + √ b) is equal to (a – √ b).
-
L’Hospital’s Rule
After you learn about derivatives in calculus, then you can use one of the most powerful tools for finding limits, L’Hospital’s Rule (L’Hospital, or L’Hôpital, is a French name, pronounced Low-pee-tal. NOT Le Hoss-pih-tal).
In order to use L’Hospital’s Rule, you must first check to see that your limit has the right form.
First of all, it must be a fraction of two functions, p(x) / q(x). If it isn’t a fraction, there still may be ways to use L’Hospital as long as you can convert the given expression into a fractional form.
Secondly — and this is crucial! — when you plug in the given x-value, the fraction must either evaluate to 0/0 or ∞/∞.
If both criteria are met, then L’Hospital’s Rule states that the limit of a fractional expression is the same as the limit after taking derivatives of the numerator and denominator. That is,

Problem 4 fits the bill. It has the form 0/0, so we can use L’Hospital’s Rule.

Infinite Limits
Sometimes the limit expression involves infinity (∞ or -∞). This can happen in two different ways.
If the values of f(x) seem to get bigger and bigger without bound as x approaches a number, then we say the value of the limit is ∞. Conversely, if the values drop without bound (getting bigger in the negative sense), then the value of the limit is -∞. In either case, the function has a vertical asymptote at that point. Read here for more information about vertical asymptotes.
The other way that infinity may play a role is that you might have a limit in which x → ∞ or x → -∞. Either case leads to a horizontal asymptote, which you may read more about in this article.
Further Resources for limits
Check out this Magoosh article or this video for more practice and explanation about limits.
Continuity
Now that we’ve discussed limits, we can talk about continuity. Intuitively, we say a function is continuous if we can draw its graph without lifting the pencil. That is, there are no jumps, holes, or vertical asymptotes in the graph. However, we need a more precise definition!
The Three-Part Definition for Continuity
A function f(x) is continuous at a point x = a if the following limit statement is true:
![]()
But wait, that doesn’t look like a “three-part” definition! Well, in fact, there are three major ideas wrapped up in that limit equation.
-
1. The limit must exist.
This means that the y-values of the graph must be tending toward some finite number as x → a. So the function cannot be continuous at a vertical asymptote or a jump, places where the limit fails to exist.
-
2. The function value must exist.
There must be a value for f(a). This means that a function is not continuous at a “missing” point of the graph (open circle).
-
3. The limit must agree with the function value.
Even if a function passes both conditions (1) and (2), it could still fail to be continuous. We want the data (function value) to fit the trend (limit). If that does not happen, then the function is not continuous at that point.
A Graphical Example
Let’s see how the three parts of the continuity definition play a role in the following problem.
- A graph of f(x) is shown below. Determine the largest set of x-values at which f is continuous. Write your answer in interval notation.
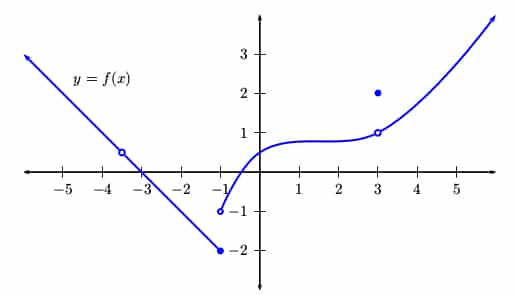
Ok, we can see three obvious “issues.” In order from left to right, there are discontinuities at x = -3.5, -1, and 3.
At x = -3.5, the function value fails to exist.
At x = -1, the limit value fails to exist.
At x = 3, the function value, f(3) = 2, doesn’t agree with the limit value, 1.
f is continuous everywhere else. Therefore, the answer is: (-∞, -3.5) U (-3.5, -1) U (-1, 3) U (3, ∞).
Final Thoughts on Limits and Continuity
Limits and continuity problems on the AP Calculus exams may be very easy or may be quite challenging. However, by keeping a few tools, definitions, and examples in mind, you can take your score to the limit!

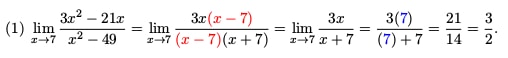
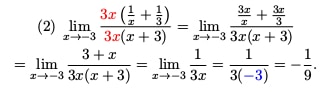
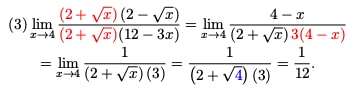
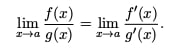
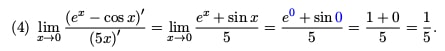



Leave a Reply