
If you’re wondering why hard ACT Math problems are so difficult, know that it’s not because they test crazy advanced topics like multivariable calculus or anything like that. Instead, it’s because they take some of the foundations of math topics you’ve already studied in school, like pre-algebra, algebra, and geometry, and turn them into multi-step processes that may combine concepts from different areas.
Does this make them challenging? Yep. Does it mean you can’t solve them? Absolutely not! To master these problems, you’ll need to refresh your understanding of the concepts, then put them into practice.
Think you’re ready to put your skills to the test? Check out the twelve ACT math challenge problems we’ve put together for you below. Answers and explanations follow!
Want to make sure you’ve mastered the trickiest concepts in all areas? For ACT challenge problems from other ACT sections, check out:
1. Let x and y be nonzero real numbers such that 2(y+1)=2x. Which of the following expresses 2(y+2)in terms of x?
A. 1/(2x3)
B. 1/(2x+3)
C. 4x
D. 8x
E. 2x3
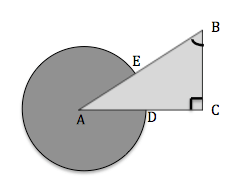
2. As shown in the figure below, A is the center of the circle, and right triangle ABC intersects the circle at D and E. Point D is the midpoint of AC, which is 22 cm long. The shaded region inside the circle and outside the triangle has an area of 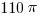 square centimeters. What is the measure of angle B?
square centimeters. What is the measure of angle B?
A. 45°
B. 48°
C. 50°
D. 54°
E. 57°
3. A box contains 50 cards.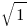 is written on the first card,
is written on the first card, 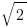 on the second,
on the second, 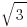 on the third and so on through
on the third and so on through 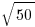 , with no numbers repeated. A card is drawn at random from the box. What is the probability that the number on the card is an irrational number?
, with no numbers repeated. A card is drawn at random from the box. What is the probability that the number on the card is an irrational number?
A. 0/50
B. 7/50
C. 25/50
D. 35/50
E. 43/50
4. Which of the following is an equation of the largest circle that can be inscribed in the ellipse with the following equation?
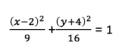
A. (x-2)2 + (y+4)2 = 81
B. (x-2)2 + (y+4)2 = 16
C. (x-2)2 + (y+4)2 = 9
D. x2 + y2 = 16
E. x2 + y2 = 9
5. What would s have to be so that 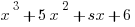 is divisible by (x + 2)?
is divisible by (x + 2)?
A. 9
B. 5
C. 2
D.-6
E.-13
6. In a geometric sequence in which all of the terms are positive, the second term is 2 and the fourth term is 10. What is the value of the seventh term in the sequence?
A. 10√5
B. 20
C. 50
D. 50√5
E. 250
7. Suzanne drove 40 miles to see her aunt and was going 20 mph. It took her 2 hours to get to her aunt’s house. Then, she left and drove another 30 miles to the pet store, but this time only drove at 10 mph. If it took Suzanne 3 hours to arrive at the pet store, what was her average speed in miles per hour for the entire car ride from her home to the pet store?
A. 10
B. 11
C. 12
D. 14
E. 15
8. Students at Thomas Jefferson High School boarded the bus for a field trip that went 15mph through a 30 mile section of the city. The bus then stopped for lunch in a suburb before continuing on a 3 hour tour of countryside at a constant speed of 10mph. Finally, the bus drove 40 miles straight back to the high school. If the students arrived back at Thomas Jefferson High School two hours later, approximately what was the average speed for the entire field trip?
A. 11
B. 12
C. 13
D. 14
E. 15
9. If sin 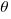 = –
= – 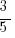 , which of the following could be true about
, which of the following could be true about 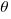 ?
?
A. 0 < 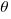 <
< 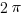 /3
/3
B. 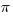 /4 <
/4 < 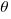 <
< 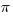 /2
/2
C. 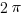 /3 <
/3 < 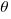 <
< 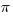
D. 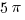 /6 <
/6 < 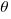 <
< 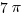 /6
/6
E. 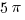 /3 <
/3 < 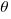 <
< 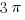
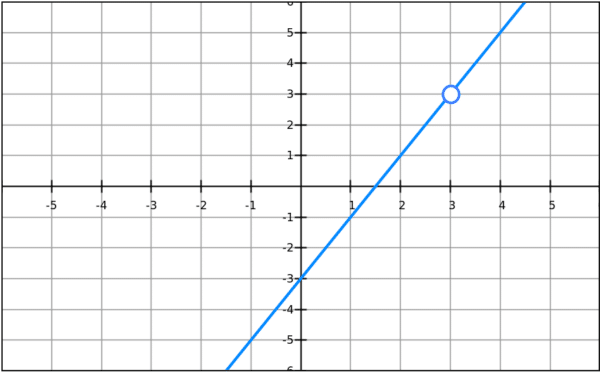
10. The graph below shows a function graphed in the standard (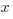 ,
, 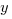 ) plane. Which of the following could be the equation of the function?
) plane. Which of the following could be the equation of the function?
A. 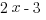
B. 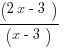
C. 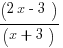
D. 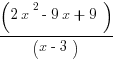
E. 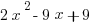 /
/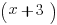
11. The function m(n) is defined by 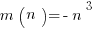 . Which of the following is the value of m(m(n))?
. Which of the following is the value of m(m(n))?
A. -n9
B. -n6
C. n3
D. n6
E. n9
12. The function values for p(x) vary directly as x for all real numbers. Which of the following best describes the graph of y = p(x) in the standard (x,y) coordinate plane?
F. A line with a y-intercept of 0.
G. A line with a y-intercept not at 0.
H. A line with no y-intercept.
J. A hyperbola.
K. Neither a line nor a hyperbola.
Answers and Explanations
1. ANSWER: C
There are two ways to solve this problem: the “math” way and the “test prep strategy” way.
Let’s talk about the test prep strategy way first. You see, this problem is a great candidate for plugging in numbers for x and y and seeing what works.
Let’s try y = 3.
Therefore 2y+1=2x becomes
23+1=2x
24=2x
16=2x
8=x
So now we have a corresponding value for x.
When y=3, the expression in the question 2y+2 equals 32. So now we have the numerical answer we are looking for in the answer choices, expressed in terms of x (which we determined equals 8.
So, plugging in 8 for x, the answer choice equivalents would be:
A. 1/1024
B. 1/19
C. 32
D. 64
E. 1024
…making our answer C.
Now let’s talk about the math way:
Using the exponent rule xm xn=xm+n, we know that
2y+1=2y 21
so we can simplify the given equation
2y+1=2x
2y 21=2x
2y=x
2y+2 would then be
2y 22
4(2y)
Since we found that x=2y we can sub in x for2y in the expression above and get our answer: C:
4x.
2.ANSWER: E
The ACT rarely gives you any unnecessary information in a math word problem. This means that all of the details in the question give you important clues that you need to solve the problem. Here’s another important tip: Whenever you are dealing with circles, and you aren’t given the radius, your first step should be to find the radius. The radius is the key to unlocking other important circle things, such as the area, circumference, sector area, or arc length.
In the case of this question, we know that AC is 22 cm, that D is the midpoint of AC, and that D serves as a point of intersection between the circle and the triangle. This means that AD is the radius and should be half of 22 cm, or 11 cm. Knowing that 11 cm is the radius allows us to find the area of the entire circle using the equation 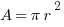 .
.
So:
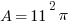
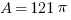
We are told in the problem that the area of the shaded region is 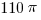 . This means that the area of the unshaded sector of the circle inside the triangle must be
. This means that the area of the unshaded sector of the circle inside the triangle must be 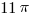 , since these two regions must add up to the total area of the circle:
, since these two regions must add up to the total area of the circle: 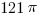 .
.
This information helps us find the fraction of the circle delimited by the triangle. Because a sector is a fraction of a circle, we can use the proportion of the area of the sector to the area of entire circle to find the degree measure of the central angle.
Because every circle has 360 degrees:
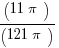 =
= 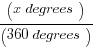
Solving this proportion to find angle A gives us x = 32.727272 repeating, or approximately 33°.
Since we know one of the other angles of the triangle is 90°, we can find the measure of the remaining angle, angle B, by subtracting the two known angles from 180° (since the angles in a triangle always add up to 180°).
180 – 90 – 33 = 57
So our answer is (E) 57°.
And for some bonus fun (particularly if you got tripped up on finding the area of the sector), check out this cool animated video we made on this topic!
3. ANSWER: E.
First of all, we need to remember what rational and irrational numbers are. Rational numbers can be expressed as a fraction; irrational numbers cannot.
Now let’s think through the question. Do you really have to go through every number from 1 to 50? The ACT will never expect you to do that, so there must be a better way.
Let’s take a look at the pattern: √1, √2, √3, √4. As soon as we get to √4, we have something that can be simplified to an integer. √4 = 2. √4 is a perfect square, and guess what? The perfect squares are the only square roots that are rational numbers. Something like √5 gets really messy because there are not two equal fractions that can be multiplied together to equal 5.
So we just need to count the perfect squares before 50. There are seven: 1, 4, 9, 16, 25, 36, 49. So that means out of our 50 numbers, 7 can be reduced to integers (or fractions) and 43 are irrational. So our answer is E.
Bonus hint: If you come across a problem like this on the ACT, and don’t know how to solve it, make sure you eliminate some answer choices! The moment you find an irrational number as you count through the series, you can eliminate answer choice A, for example. And this happens really quickly: √2 is an irrational number. You can also take a logical guess if you just work through the first 11 numbers. You should find that out of the first 11, 8 numbers are irrational. This definitely eliminates B, and thinking logically, you could probably take a guess that the overall probability is going to be high.
4. ANSWER: C
This question is difficult primarily because you need to have some higher-level knowledge of the equations of circles and ellipses. If you just studied these in school, then it wouldn’t be nearly as tough. But because equations of ellipses and circles are fair game for higher-level questions on the ACT, we thought we’d feature one here in our Challenge series!
So let’s get started with the equation for an ellipse:
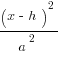 +
+ 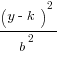 = 1
= 1
 +
+ 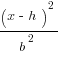 = 1
= 1
If an ellipse is wider than it is tall, our equation looks like the first one. If it is taller than it is wide, it looks like the second one. The a always goes with the variable whose axis parallels the wider direction of the ellipse, and the b always goes with the variable whose axis parallels the narrower direction, hence the reason for the difference in the equations.
In our problem, we have an ellipse that is taller than it is wide. What’s important is that you visualize what an ellipse like this looks like:

If we put a circle inside this shape, it can only have a diameter that is as wide as the ellipse is wide, otherwise it wouldn’t fit.

Okay! Back to the ellipse equation:
h and k tell us where the center of the ellipse is, so our center is (2,-4). a and b tell us how many units away from the center each vertex is. Since a is 3 and b is 4, we know that our ellipse is 6 units wide and 8 units tall.
If we put a circle in this ellipse, this means it cannot have a radius greater than 3.
The equation of a circle is:
(x-h)2 + (y-k)2 = r2
So we need to see 32, or 9, in our answer choice for the radius of the circle, making our answer C.
5. ANSWER: A
Probably the most elegant way to solve this problem is to remember the Factor Theorem. This is a useful trick for problems like this on the ACT. The Factor Theorem states that a polynomial P(x) is divisible by binomial (x – c) if and only if P(c) = 0. In order for a polynomial to be divisible by a linear binomial, the polynomial and the binomial must have the same root.
If we want polynomial P(x) to be divisible by (x + 2), it must be true that P(– 2) = 0. In other words, x = -2 must be a root of the equation.
P(x) = x3 + 5x2 + sx + 6
P(-2) = -23 + 5(-2)2 + s(-2) + 6 = 0
-8 + 5*4 – 2s + 6 = 0
-8 + 20 + 6 = 2s
18 = 2s
9 = s
So our answer is A.
6. ANSWER: D
In a geometric series, each term is the product of previous term times some common ratio. We multiply by the common ratio to change any one term into its successor.
Here, we don’t know the common ratio, so let it be r.
a2=2
a3=2r
a4=2r2
But we know the numerical value of the fourth term.
2r2=10
r2=5
r=√5
Because every term is positive, we don’t have to consider the negative square root. Now that we have the common ratio, we can move from term to term. Each time, we multiply by the square root of 5.
a4=10
a5=10√5
a6=(10√5)=10*5=50
a7=50√5
So our answer is D.
7. ANSWER: D
Average Speed = Total Distance / Total Time.
40 miles + 30 miles so the Total Distance was 70 miles. Suzanne drove for 2 hours + 3 hours so the Total Time was 5 hours. 70/5 = 14.
The Average Speed for the whole trip was 14 mph. The correct answer is (D).
Notice how the test-maker has made this problem tricky! The average speed in this problem is 14 mph, which is different from simply taking the mean of the two speeds. If we had just averaged the two speeds (10mph and 20mph) we would have gotten 15mph. Average Speed is a weighted average. Since Suzanne spent more time in the problem going 10mph than 20mph, it makes sense that the Average Speed would be closer to 10mph.
8. ANSWER: D
To find the average speed of the bus, we know we will need to find the Total Distance and the Total Time, so we can start by using another formula (Distance = Rate x Time) to help us find the pieces we’re missing for each part of the trip.
For the first part of the field trip: 30 miles = 15mph x T, so we know that T = 2 hours. For the middle part of the trip, we know that D = 10mph x 3 hours, so we know that D = 30 miles. For the last part of the trip, we know that 40 miles = R x 2 hours, so we know that R = 20mph. Now we can find the Total Distance and the Total Time:
Total Distance = 30 miles + 30 miles + 40miles = 100 miles.
Total Time = 2 hours + 3 hours + 2 hours = 7 hours.
The Average Speed = 100 miles/ 7 hours = 14.28mph. Since the question used the word “approximately,” we can round to the nearest integer: 14. The correct answer is (D).
9. ANSWER: E
This is a hard problem. First of all, notice that the angle must be in QIII or QIV, since the sine is negative. It has to be a value on the line 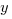 = –
= – 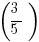 . The first three choices are all in QI and QII, so the angle can’t possibly be in any of those. We can easily eliminate (A) & (B) & (C).
. The first three choices are all in QI and QII, so the angle can’t possibly be in any of those. We can easily eliminate (A) & (B) & (C).
Let’s think about the last two. First, option (D). This option is in QII and QIII, so the part in QIII might go down low enough to contain the angle. The lowest ray in that region is at 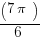 .
.
Technically, this ray isn’t even included, because it’s the endpoint of an inequality, but we will just use this value. Sine is positive in QII, zero at the negative x-axis, and starts to get more and more negative as we go around through QIII. How low does this go by this last value?
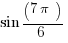 = –
= –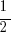 =
= 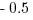
This does not go down as far as
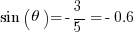
Here’s a diagram with region (D) and the line  = –
= – 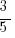 .
.
So, we can eliminate (D).
This leaves (E) by the process of elimination, but let’s verify that this works. Region (E) is in QIV. The sine is negative one at the bottom, where the unit circle intersects the negative y-axis. As we rise from this bottom, we get negative values of smaller and smaller absolute value, until it equals zero at the positive x-axis. We have to know how low the lowest values in this region are. Well, the limiting value is 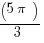 .
.
We know that 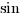
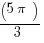 = –
= – 
Now, if you happen to have the decimal approximations memorized, you will see that:
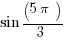 = –
= – 
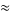
If you don’t have this decimal equivalent memorized, you could think about the triangles in QIV:
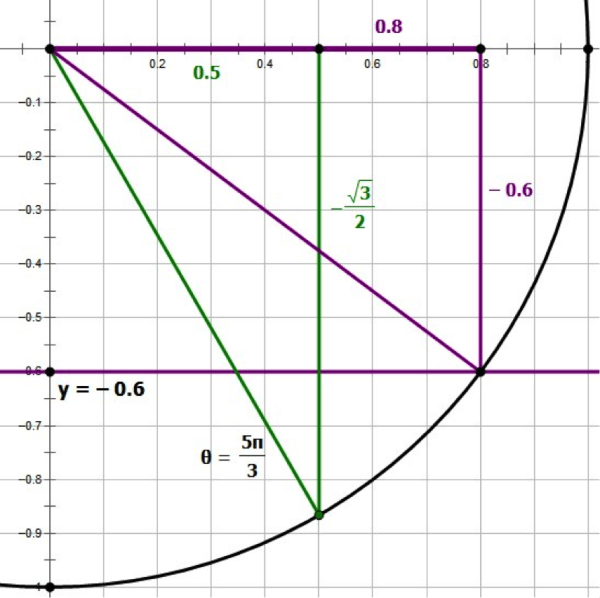
Even if we can’t directly compare the sizes of the two vertical legs, we definitely can compare the two horizontal legs, and 0.8 is definitely bigger than 0.5. That means the purple {0.6, .8, 1} triangle is further around in the counterclockwise direction from the green 30-60-90 triangle, and the point with a sine of – 0.6 would clearly be included in the arc from the 30-60-90 triangle up to the positive x-axis.
Answer = (E)
10. ANSWER: D
The graph clearly has a hole, a point discontinuity, at x = 3. This means that the function cannot be defined at x = 3. It must have (x – 3) in the denominator. On this basis, we can eliminate (A), (C), and (E).
Notice that the graph is identical to the line y = 2x – 3 at every point except for the point discontinuity at x = 3. Also, to get a point discontinuity instead of an asymptote, we need to have a factor of (x – 3) in both the numerator and the denominator. Choice (B) at x = 3 has a zero denominator and a non-zero numerator, which is the condition for a vertical asymptote. We have eliminated the other four answers, so it would seem that (D) is the answer, but let’s verify this.
In order to get a graph that is identical to y = 2x – 3 at every point except for x = 3 and has a point discontinuity at x = 3, we would have to multiply (2x – 3) by (x – 3) over itself.![]()
So everything checks out and our answer is (D)!
11. ANSWER: E
When we have functions inside functions, we call these “nested” functions – it’s important to always start from the innermost parentheses and work your way out. The expression m(m(n)) starts with an inntermost “m(n)” that we know equals -n3, so let’s start by substituting that in. Now the question is asking, what is the value of m(-n3). Just like we normally do for any f(x) function, we will plug whatever in inside the parentheses in for the variable in the function. Here, the testmaker is trying to confuse you by using the same variable “n,” but we’re too smart for the ACT’s tricks! 🙂
m(-n3) = -(-n3)3
According to the order of operations, or PEMDAS, we’d start with what is inside the parentheses. Since we don’t know the value of “n” we cannot simplify -n3 any further. Next, we simplify the exponents. Here’s where knowing your exponent rules really come in handy! When two exponents are separated by a parenthesis, we must always multiply them.
m(-n3) = -(-n9)
Remember that in number properties, any negative number raised to an odd exponent will stay negative, since it takes a pair of negatives to cancel each other out and become positive. -n9 will stay negative until it is multiplied by the -1 in front of the parentheses. Finally, we arrive at our answer:
m(-n3) = n9
The correct answer is (E).
12. ANSWER: F
The function values for p(x) vary directly as x for all real numbers. The graph of y=p(x) in a standard (x,y) coordinate plane is a line with a y-intercept at 0. Since y = p(x) doesn’t have any coefficients, and p(x) varies directly with x (like p(x) = x, as opposed to something like p(x) = 2x), this line will cross the origin (0,0). The correct answer is (F).
Want more sample problems? Check out this ACT math practice!






Leave a Reply