Ratios are one of those concepts that can pop up in just about any GRE problem. You could have the ratio between two angles that form from intersecting lines. You could have the ratio of rates a person drove at. With such a broad application, ratios are one of the concepts it is imperative you learn now.
To see how ratios work – and to see the type of problems the GRE will devise to try to trick you – let’s try a few simple problems first and then some challenging ones.
GRE Ratio Practice Problem
1. Tom is selling apples and oranges. The ratio of apples to oranges in his cart is 3:2. If he has 12 oranges, how many apples does he have?
(A) 2 (B) 3 (C) 8 (D) 18 (E) 30
Solution:
A ratio is basically a fraction that has been reduced as much as possible. In this problem the ratio 3:2, can be represented as 3/2. One way to solve this problem is to set up a simple equation:
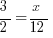
Notice I placed the 12, the number of oranges, in the denominator. We have to make sure that the number 12 corresponds to 2, the oranges in the ratio. Solving for x, we get 18 (D).
An even quicker way is to notice that we have (x6) the oranges (from 2 we go to 12) so we just have to (x6) the apples in the ratio: 3 x 6 =18.
Now’s let’s try the same question but with a spin:
2. Tom is selling apples and oranges. The ratio of apples to oranges in his cart is 3:2. If he has a total of 30 fruits, how many apples does he have?
(A) 2 (B) 3 (C) 12 (D) 18 (E) 30
Solution:
This question, while essentially the same, is the one that gives students a lot more trouble. The problem is combining two concepts: ratio and total. To do so simply add the ratios. We have 3:2 so the total is 5.
One way to solve the problem is to set up the table. Tables are great both from a teacher’s and beginner’s standpoint. In this case, I get to show you a nice, tidy way of solving the problem and you have an easy way both to conceptualize and solve the problem.
However, once you become used to tables, in the interest of time, learn to solve a ratio without one (I’ll show you how to do so in a second!).
| Apples | Oranges | Total | |
|---|---|---|---|
| Ratio | 3 | 2 | 5 |
| M(x) | |||
| Actual | ? | ? | 30 |
What do we multiply the total ratio by to get the actual total? (x6).
So in the middle row in the total column we can place a 6.
| Apples | Oranges | Total | |
|---|---|---|---|
| Ratio | 3 | 2 | 5 |
| M(x) | 6 | 6 | 6 |
| Actual | 18 | 12 | 30 |
Notice the (M)x, which stands for multiply (you can dispense with the M, I just didn’t want anyone thinking there is this random variable x floating around).
Now we multiply the apples and oranges by 6 to get 18 and 12, respectively.
Remember the faster way I mentioned?
- Add the ratio
- Figure out the x6
- Multiply 3 x 6
18 (D). Also remember not to mix up apples and oranges. A classic trick on the GRE is they reverse the order.
Practice Questions
Okay, you’ve got the hang of ratios. Now you want something a little more challenging. Voila – it’s the ratio challenge workout.
The problems below appear superficially similar. Yet, the math behind each is different. Nonetheless, each of them deals with ratios, and will put your ability to the test. The problems tend to get progressively harder. So if you struggled at the end, don’t despair. As long as you can nail the first three, you’re doing pretty well on ratios.
Good luck!
1. A jewel necklace contains only emeralds, rubies, and diamonds. If the ratio of emeralds to diamonds is 2:7 and the ratio of diamonds to rubies is 3:2, then which of the following could not be the number of jewels on the necklace?
(A) 41
(B) 81
(C) 82
(D) 123
(E) 205
2. A tiara is studded with a mixture of gems. The ratio of sapphires to emeralds is 3:1. If 6 emeralds are added, the tiara will contain an equal number of sapphires and emeralds. How many emeralds must be added to the original tiara so that the ratio between emeralds and sapphires is 3:1?
(A) 9
(B) 12
(C) 18
(D) 24
(E) 27
3. An imperial scepter is mounted with diamonds, rubies, emeralds, and sapphires in the ratio of w : x : y : z. If w, x, y, and z are distinct single digit primes, then how many gems could be on the imperial scepter if it only contains the gems listed above?
(A) 19
(B) 58
(C) 85
(D) 97
(E) Cannot be determined from the information provided above.
4. (Okay – enough with the jewels!) Marty has a coin collection, which consists of only New World and Old World coins, in a ratio of 3:1. Marty’s friend Kyle swaps 28 of his Old World Coins for 28 of Martin’s New World coins. If Marty now has as many Old World coins as he does New World coins, how many coins did Marty originally have in his collection?
(A) 28
(B) 84
(C) 112
(D) 130
(E) 390
5. (Okay, back to jewel necklaces). Marty has a necklace that contains a total of 36 rhinestones, zirconium, and obsidian “gems.” If the ratio of obsidian to zirconium is 2:5, then which of the following could not be the number of rhinestones in Marty’s necklace?
(A) 8
(B) 12
(C) 15
(D) 22
(E) 29
Answers:
1. B
2. D
3. C
4. C
5. B
Special Note:
To find out where ratios sit in the “big picture” of GRE Quant, and what other Quant concepts you should study, check out our post entitled:
What Kind of Math is on the GRE? Breakdown of Quant Concepts by Frequency






Leave a Reply