Perhaps you recall with more than a little dread your high school geometry class: fifteen-step proofs and the law of cosines were two things you were certain you’d never see again. Well, if you are taking the GRE, you were by no means mistaken—proofs and indeed all of trig are nowhere to be found on GRE math.
That doesn’t mean that the GRE is void of geometry. Below are the GRE geometry rules and geometry formulas you have to know. This list is by no means exhaustive, but for must-know concepts you’ve come to the right place.
GRE Geometry Formulas
- GRE Geometry Formulas At a Glance
- Sample GRE Geometry Formula Practice Questions
- GRE Geometry Formulas In Depth
- GRE Geometry Formulas FAQ
If you’re interested in more than geometry, try our more general GRE Math Formula eBook!
GRE Geometry Formulas At a Glance
Need to see the key geometry formulas in one place? You’re in luck! Here’s a list of geometry formulas you’ll need on test day. Bookmark this page, and read on for more in-depth explanations of each geometry formula.
| Category | Rule/Formula |
|---|---|
| Angles |
Click here for all rules
|
| Triangles |
Click here for all rules and formulas
|
| Circles |
Click here for all rules and formulas
|
| Parallelograms |
Click here for all rules and formulas
|
| Polygons |
Click here for all rules and formulas
|
| 3-D Shapes |
Click here for all formulas
|
Sample GRE Geometry Formula Practice Questions
Those are it in a nutshell—the GRE geometry formulas you’ll need on test day! However, memorizing formulas and putting them into practice are two very different things.
So that you can see the difference, we’ve pulled two problems from the Magoosh GRE prep course so you can try your hand at them.
Question 1: Multiple Choice
A. 26
B. 32
C. 40
D. 64
E. 80
Question 2: Numeric Entry
GRE Geometry Formulas In Depth
Geometry Rules: Angles and Lines
A right angle is made up of 90 degrees. A straight line is made up of 180 degrees.
Click here to learn more about angles and lines
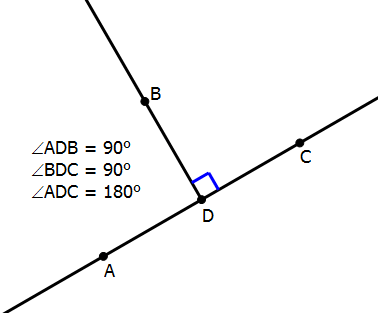
In this diagram, ADC is a straight line. BTW, make sure you don’t confuse “straight” lines with “horizontal” lines. Any line that doesn’t bend or curve is “straight,” regardless of direction. By contrast, a “horizontal” line is parallel to the top or bottom of the page, parallel to the distant horizon. Line ADC is “straight” but not “horizontal.”
Notice, also, that “straightness” is one of the very few things we can assume on the GRE. If it looks like there’s no bend in the line, then there’s no bend: i.e. if it looks straight, it is straight. By contrast, we cannot assume perpendicularity: if we didn’t have that special little blue square guaranteeing that the lines were perpendicular, we could not assume that either angle ADB or angle BCD were right angles. That is something we must be told, in one form or another.
If two lines intersect, the sum of the resulting four angles equals 360°. Furthermore, the angles opposite each other have to be equal. These angles meet at just a vertex, so they are called “vertical” angles (a term you may remember but don’t need to know).
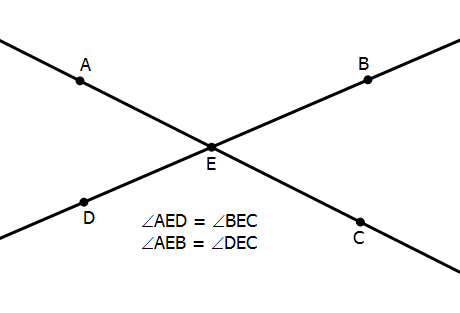
If we were told, say, that angle AED equals 40°, then immediately we would know the measures of the other three angles: angle BEC would have to equal AED, so that would also be 40°, and the other two angles would have to be the supplements of 40°. The supplement of an angle is 180° minus the angle. Thus, angle AEB = angle DEC = 140°; two angles that add up to 180° are supplementary. This way, all four angles add up to 360°.
When a line intersects a set of parallel lines, we get many more angles. We get eight angles: four “big” angles and four “small” angles. There are a number of technical names (“alternate interior angles”) that we don’t have to know for GRE geometry. We just have to know that every big angle is equal, every small angle is equal, and any big angle and any small angle are supplementary.
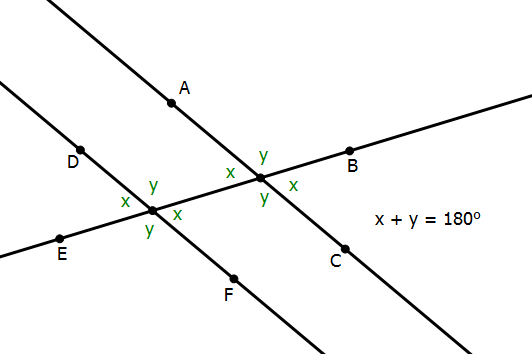
In the diagram, AC is parallel to DF: we could write that fact as AC // DF. That we cannot assume: we would have to be told that two angles are parallel. Once we are told that, and a third line intersects them, we get all the equal angles. Here, all the small angles are called x, and all the big angles are called y, and of course, x + y = 180°.
Geometry Rules: All Triangles
A triangle is a shape with three line segment sides.
Facts about all triangles:
In any triangle, the sum of the three angles is 180°.
That’s a big idea that Mr. Euclid (c. 300 BCE), the great geometer, first proved. Here’s another important geometry equation:
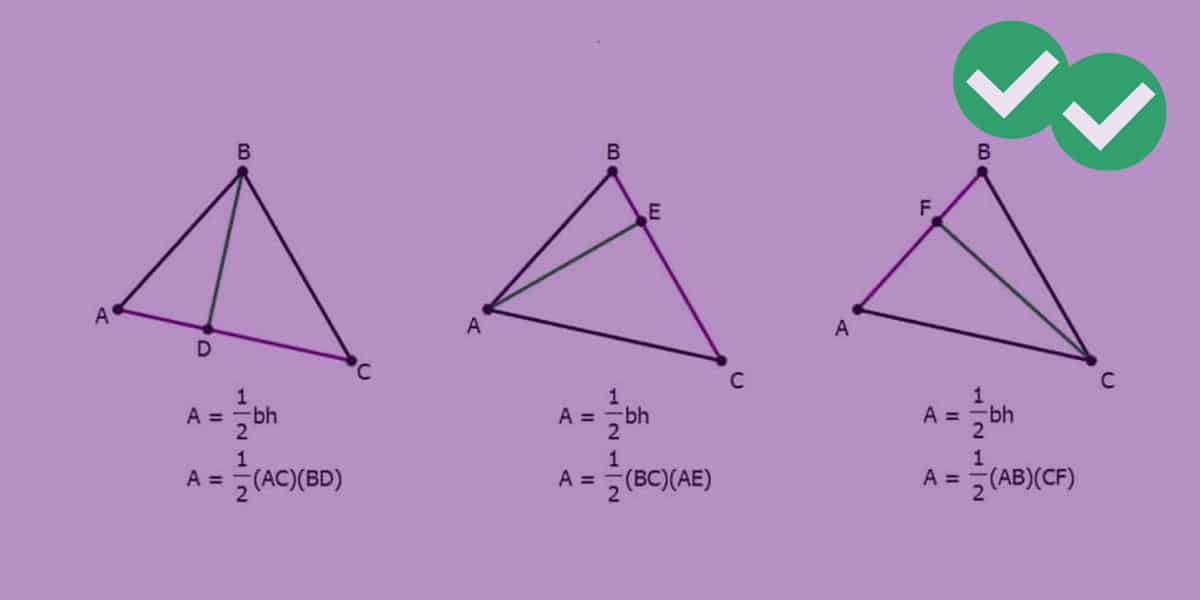
\(\text{Area}=\frac{1}{2}\times\text{bh} \)
Click here to learn more about triangles
There’s more to that simple formula than means the eye. The letter b stands for the base: what’s the base of a triangle? Naïvely, folks will say the “bottom,” the horizontal side, is the base, but that’s not the whole story. In fact, any of the three sides can be the base. Similarly, the letter h is height: by “height,” we mean the length of a segment known as an altitude. An altitude is a line that passes through a vertex and is perpendicular to the side we are considering the base. Thus, for any triangle, we potentially have three different b & h combinations that would allow us to calculate the area.
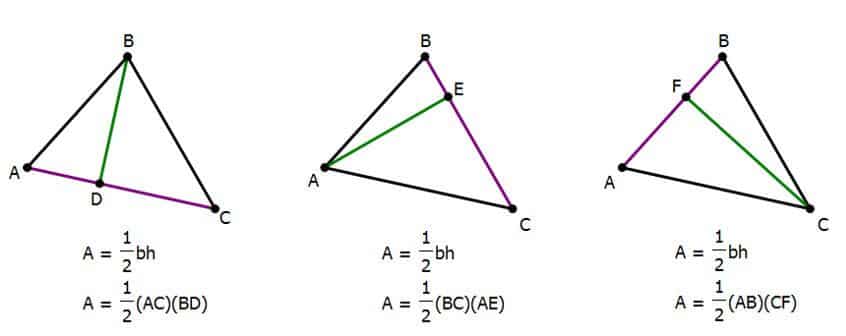
Now, of course, the GRE is unlikely to give you all that information, three side lengths and three altitudes, in the course of a geometry problem. If a GRE geometry question ask for the area of the triangle, it will provide a way to find at least one base and the corresponding height. Keep in mind that the altitude divides the triangle into two little right triangles, so the Pythagorean Theorem (below) may be involved in finding some of the necessary lengths.
The sum of any two sides is greater than the third. If one side is 3 and one side is 5, call the third side x. We know that x + 3 > 5, which means that x > 2—this means that x could be 2.01, because it doesn’t have to be an integer. We also know that 3 + 5 > x, or 8 > x; again, x could be 7.999, as long as it’s less than 8. Thus, x has to be between 2 and 8, so it could be an integer {3, 4, 5, 6, 7} or it could be any fraction or decimal in that range. Remember that numbers are not necessarily integers on the GRE.
The largest side is always opposite the largest angle, and the smallest side is always opposite the smallest angle.

In this diagram, PQ is clearly the shortest side, so angle R has to be the smallest angle. Similarly, PR is longest side, so angle Q must be the largest angle.
Geometry Rules: Isosceles Triangles
One geometry rule related to this last fact concerns one elite category of triangles: the isosceles triangles. These are triangles with two equal sides.
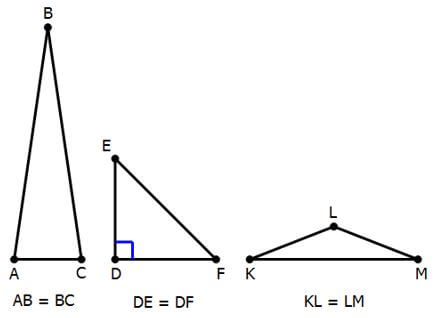
The angle between the two equal sides may be
(a) an acute angle (less than 90°), as in triangle ABD
(b) a right angle, as in triangle DEF, or
(c) an obtuse angle (greater than 90°) as in triangle KLM
Click here to learn more about isosceles triangles
If two sides are equal, then we know the opposite angles are also equal: in triangle ABC, angle A = angle C; in triangle DEF, angle E = angle F; and in triangle KLM, angle K = angle M. In fact, Mr. Euclid pointed out that this geometry rule works both ways: if we are told two sides are equal, then we know two angles are equal, and if we are told two angles are equal, we know two sides are equal.
The line down the middle of an isosceles triangle is special:
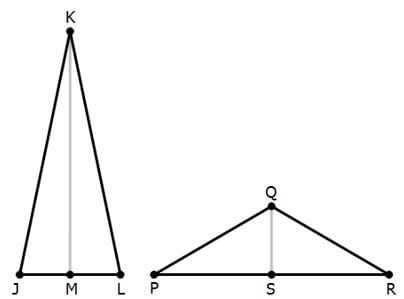
As long as we are told that JKL and PQR are isosceles triangles, then this midline has some special properties:
(a) it is perpendicular to the base: angle KML = angle QSR = 90°
(b) its lower point bisects the base: JM = ML and PS = SR
(c) it bisects the upper angle: angle JKM = angle MKL, and angle PQS = angle SQR
These are all good geometry equations to associate with isosceles triangles.
Super-technically, an isosceles triangle is one that has at least two equal sides. This means that a very special case of isosceles is the equilateral triangle.
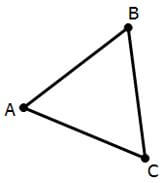
All three sides have equal length and each angle equals 60°. This is the most symmetrical triangle. Be careful not to assume that a triangle is equilateral: you cannot assume one is equilateral just because it appears as one. You would have to be told about either three equal lengths or all 60° angles.
Geometry Rules: Right Triangles
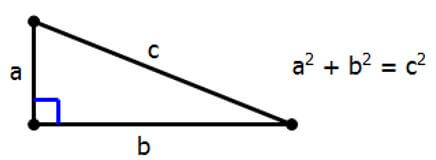
Any right triangle has two sides touching the right angle: these are called legs. The longest side, always opposite the right angle, is called the hypotenuse.
One geometry rule that applies to all right triangles is theorem named for Mr. Pythagoras (570 – 495 BCE), whom some scholars consider the first mathematician.
Click here to learn more about right triangles, the 30-60-90 triangle, and isosceles right triangle
Notice that the side we call “c,” the side alone on one side of the equation, has to be the hypotenuse. Also, notice that we can apply this formula unless we know a triangle is a right triangle, and that is not something we can assume simply from looks. If we get the litter perpendicular square, as we have here, then we know it’s a right triangle and we can apply this geometry equation.
Of course, some or all of the sides of a right triangle can be decimals, but it is possible, in special cases, for all three sides to be integers. These are sets of three integers that satisfy the Pythagorean Theorem. The most common is {3, 4, 5} and its multiples, but other good ones to recognize are {5, 12, 13}, {8, 15, 17}, and {7, 24, 25}.
There are two very special triangles that you have to understand for GRE geometry. The first is the 30-60-90 triangle:
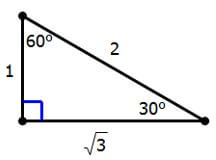
We can multiply these lengths by any multiple, but they are always in this ratio. The short side, opposite the 30° angle, is always half the hypotenuse. The longer leg is always the square root of 3 times longer than the shorter leg. The ratios and angles in this triangle come direction from an equilateral triangle that was cut in half.
The other triangle is the 45-45-90 triangle, also known as the Isosceles Right Triangle.
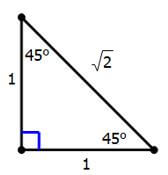
Again, the ratios always are the same and we can multiply by any number. The two legs are always equal because this is an isosceles triangle, and the hypotenuse is always the square-root of two times any leg. GRE loves all the geometry formulas associated with these two triangles.
Geometry Formulas: Circles
pi describes the ratio of any circle’s circumference (c) to its diameter (d). This number, pi, can be approximated by the decimal 3.14 or by the fraction 22/7, but it is a really a decimal that goes on forever with no repeating pattern.
The distance from the center out to the circle in any direction is called the radius (r). Here are the first few geometry formulas associated with the circle:
\(d=2r\)
\(c=πd\)
\(c=2πr\)
The first is just the fact that any diameter can be thought of as two radii in 180° opposite directions. The second is just a restatement of the definition of pi, given above. The third results from plugging the first into the second, and it’s actually the most useful formula for circumference, as we shall see.
Then, there’s another famous geometry equation, the formula for the area of a circle:
\(\text{Area}=π\text{r}^2\)
Click here to learn more about circles
Archimedes (287 – 212 BCE), one of the greatest mathematicians of all times, gave us this remarkable formula.
We can divide a circle or its area up into pieces. Either a piece of the circle or a piece of the area would depend on the central angle, which is a part of the 360° all the way around the circle.
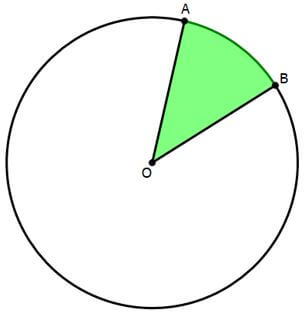
The curvy line from A to B, the path along the curve of the circle, is called an arc: this is a “piece” of the circumference. An arc is like the crust of a slice of pizza. The shaded area, which is like the whole slice of pizza, is called a sector. A sector is a piece of the whole area. We calculate either by setting up a geometry formula that compares two part-to-whole ratios, one of which involves the central angle, AOB.
\(\frac{∠AOB}{360°}=\frac{;\text{length of arc AB}}{2πr}\)
\(\frac{∠AOB}{360°}=\frac{;\text{area of sector AOB}}{π\text{r}^2}\)
These are two geometry formulas that you should not need to memorize: you should be able to figure them out by setting up part-to-whole ratios.
Geometry Formulas: Quadrilaterals
A quadrilateral is a shape with four line segment sides.
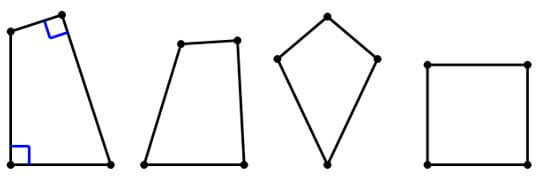
In the first, an irregular quadrilateral, we are given that two angles are right angles. The last one looks like a square, but of course, we can’t assume either equal sides or 90° unless we are told.
The only geometry rule that applies to all quadrilateral is the fact that the sum of the four angles in any quadrilateral is 360°.
Geometry Formulas: Parallelograms
A parallelogram is a quadrilateral with two pairs of parallel sides.
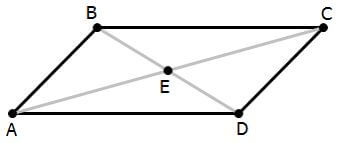
Any parallelogram has four amazing properties that always go together
(1) opposites sides are parallel: AD // BC and AB // CD
(2) opposites sides are equal: AD = BC and AB = CD
(3) opposite angles are equal: angle BAD = angle BCD and angle ABC = angle CDA
(4) diagonals bisect each other: AE = EC and BE = ED
The diagonals of any quadrilaterals are the lines connecting opposite vertices: here AC and BD are the diagonals.
Those four are the “BIG FOUR” parallelogram properties. If any of them is true, all the others automatically have to be true. Once you know it’s a parallelogram, you get a boatload of geometry formulas you can use.
Click here to learn more about parallelograms
The area of a parallelogram can be tricky. It’s just A = bh, but we have to be careful: the base b is a side, but the height h is the distance between two parallel bases.
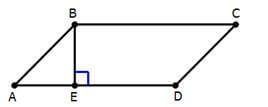
In the diagram, we could consider either AD or BC the base (they are equal!) and BE would be the height. What if we are not given the height? Well, notice that ABE is a right triangle, in which the Pythagorean Theorem would apply: for example, if we knew AE and AB, we could find BE with the Pythagorean Theorem.
As a general rule, whenever a diagram has some vertical lines, some horizontal lines, and some slanted lines, and you have to find a particular length, chances are very good that there’s a right triangle somewhere in the diagram you can use to find the length you need! The Pythagorean Theorem is a truly remarkable geometry formula: it shows up all over the place!
Geometry Formulas: Special Parallelograms
There are three categories of special parallelograms: rhombuses, rectangles, and squares. The BIG FOUR parallelogram properties above apply to all of them.
Click here to learn about rhombuses
A rhombus is an equilateral quadrilateral, that is, a quadrilateral with four equal sides.
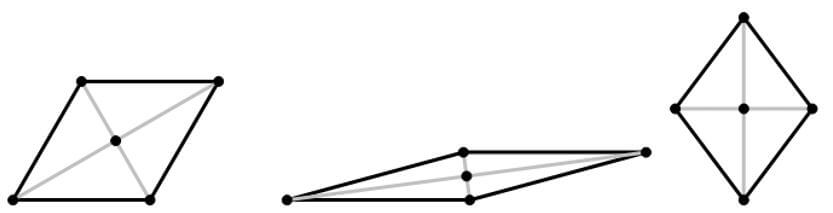
Most “diamond” shapes, such as those on playing cards, are simply rhombuses turned sideways, like the one on the right above. If the side is s, then the perimeter is always just 4s. The diagonals of a rhombus are always perpendicular. In fact, any rhombus can be subdivided into four congruent right triangles.
As with a general parallelogram, A = bh, where the b is any side and the h is the length of a perpendicular segment: as with a general parallelogram, the Pythagorean Theorem may play a role in finding one of the lengths that you need.
(A pedantic note: the correct plural of “rhombus” is “rhombuses.” You see, words that end in –us from Latin can take the Latin ending –i in the plural: these would be words such as “syllabus/syllabi,” “focus/foci,” etc. Words with the –us ending from Greek do not use the Latin plural: hence “rhombus/rhombuses,” “octopus/octopuses“, “hippopotamus/hippopotamuses,” etc. Obviously, much confusion circulates in colloquial speech about these finer points.)
Click here to learn about rectangles
A rectangle is an equiangular quadrilateral, that is, a quadrilateral with four 90° angles.

Each angle is 90° and the two diagonals are always equal in length: it’s an old carpenter’s trick to verify that a doorframe has four right angles simply by checking the lengths of the two diagonals. Of course, it’s usually easy to find the length of a diagonal using the Pythagorean theorem.
The area of a rectangle is simply A =bh, where the base & height are simply lengths of any two adjacent sides. The perimeter is P = 2b + 2h.
Click here to learn about squares
Finally, we get the square. The fact that the square is one of the most familiar shapes, one of the first shapes learned in one’s early years, profoundly obscures how elite and sophisticated a shape it is. A square is a quadrilateral, a parallelogram, a rhombus, and a rectangle—and it has all the properties of all those categories, including four equal sides and four 90° angles. If the side is s, then
\(\text{Area} = s^2\)
\(\text{Perimeter}=\text{4}\times\text{s}\)
\(\text{Length of diagonal}=\text{s}sqrt{2}\)
If we know a shape is a square, if we are told that it is a square, then all these geometry rules apply to the shape. BUT, just because something looks close to a square doesn’t mean that it is a square! Remember, no GRE geometry diagram is guaranteed drawn to scale, so if we are not given some explicit guarantee, something drawn to look like a square might be any quadrilateral!
Geometry Formulas: Higher Polygons
A polygon is any closed figure with three or more line-segment sides. We have already discussed triangles and quadrilaterals. Here is a handy chart for the names:
| Number of sides | Name |
|---|---|
| 3 | triangle |
| 4 | quadrilateral |
| 5 | pentagon |
| 6 | hexagon |
| 8 | octagon |
| 10 | decagon |
For any n-sided polygon, the sum of all the angles in the polygon is given by sum = (n – 2)(180°). Any triangle has a sum of 180°, any quadrilateral has a sum of 360°, any pentagon has a sum of 540°, etc.
Click here to learn more about higher polygons
Another important idea is the idea of a regular polygon. This is a particularly tricky word: in ordinary speech, “regular” means ordinary, commonplace. In geometry, it has almost the opposite meaning. The regular polygons are the most elite and symmetrical shapes. A regular polygon is one that has all equal sides and all equal angles. The “regular triangle” is the equilateral triangle, and the “regular quadrilateral” is the square. In a regular polygon, because we can compute the sum of the angles, we can divide this by the number of angles to get the individual angle measure.
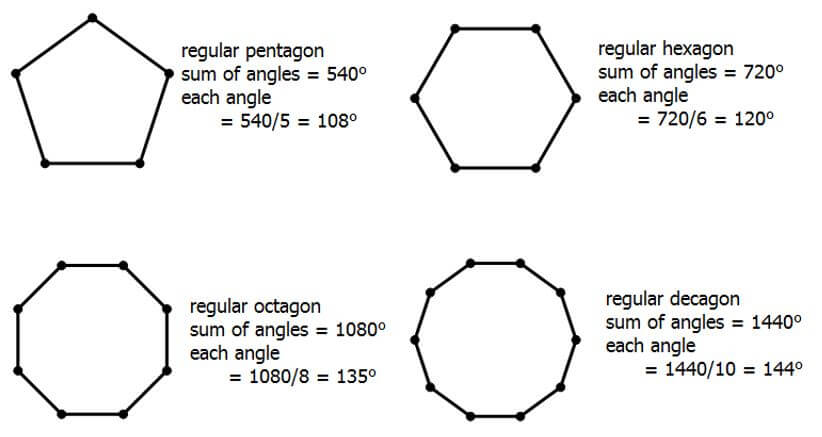
The regular octagon, of course, is the stop sign shape in many countries around the world.
As we saw above, quadrilaterals have two diagonals. Pentagons have five, and higher polygons have many more. See this post about the diagonals of a regular octagon. The diagonals of the regular pentagon trace out the standard five-pointed star, such as the stars on the flag of the United States of America.
Geometry Formulas: Three-Dimensional Shapes
A rectangular solid is a box-shape: it has six faces that are rectangles, and all the faces meet at right angles. Let’s say that it has a height of h, a length of l, and width of w. Then the volume and surface area would be:
\(V=lwh\)
\(SA=2lw+2wh+2lh\)
The surface area is simply the sum of the areas of the six rectangular faces.
Click here to learn about cubes, cylinders, cones, and spheres
If all the lengths of a rectangle solid are equal, then it’s a cube. A cube has six congruent square faces that all meet at right angles to each other. If the edge length is s, then
\(\text{V} = s^3\)
\(\text{SA} = 6s^2\)
All the 3D shapes that involve a circle were figured out by Archimedes (287 – 212 BCE), including the cylinder and the sphere. The volume of a cylinder can be thought of as base times height, where the “base” is the area of the circular base.
\(\text{V} = πr^2\text{h}\)
The GRE does not expect you to memorize the formulas for cones and spheres. If the GRE were to ask about these shapes at all, it would have to give you the formula and then expect you to do some calculation or algebraic manipulation with it. It’s good to be generally familiar with those formulas, enough so that they are not strange and intimidating, but you do not need to memorize them. If you’re curious, here they are:
Cone
\(\text{V} = \frac{1}{3}πr^2\text{h}\)
Sphere
\(\text{V} = \frac{4}{3}πr^3\)
\(\text{SA} = 4πr^2\)
Geometry Formulas: Coordinate Geometry
A line in the coordinate plane can be represented in a few ways: the most common is slope-intercept form:
y = mx + b
The b is the y-intercept, the place where the line intersects the y-axis. The m is the slope. Slope is an indication of how tilted a line is. The slope of a horizontal line is zero. A vertical line has infinite slope. A 45° line has a slope of m = 1. To find the slope between two points A & B, draw a slope triangle:
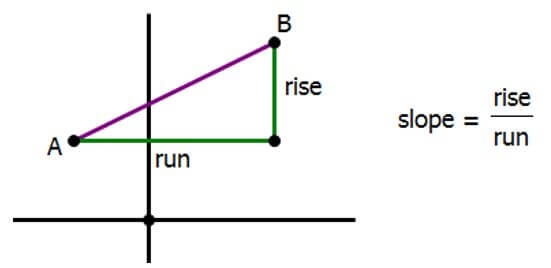
If you do even a rough sketch, you should be able to read the rise and run off the graph, and then slope is just rise over run. Keep in mind, there are a few ways to think about any slope.
Click here to learn more about coordinate geometry
A slope of m = +3 means any of the following:
(a) to the right one unit, up 3 units
(b) any multiple of (a) (e.g. right 7 units, up 21 units)
(c) to the left one unit, down 3 units
(d) any multiple of (b) (e.g. left 5 units, down 15 units)
A slope of m = – 5/3 means any of the following:
(a) to the right 1 unit, down 5/3 of a unit
(b) to the right 3 units, down 5 units
(c) any multiple of (b) (e.g. right 9 units, down 15 units)
(d) to the left 1 unit, up 5/3 of a unit
(e) to the left 3 units, up 5 units
(f) any multiple of (e) (e.g. left 18 units, up 30 units)
The geometry rules concerning slope are very important to remember.
To find the y-intercept, set x equal to 0 and solve for y.
To find the x-intercept, set y equal to 0 and solve for x.
Parallel lines have equal slopes. Perpendicular lines have slopes that are opposite-signed reciprocals: for example, if the slope of one line is – 3, the slope of the perpendicular line is + 1/3; if the slope of one line is +4/7, the slope of the perpendicular line is – 7/4.
Finally, there is a thing out there called the “distance formula” for coordinate geometry, but we are not going to state it here, because it is an abomination before God and man. It makes monstrously difficult something that is quite straightforward. Here’s how to find distance between any two points. Again, draw or sketch the slope triangle:
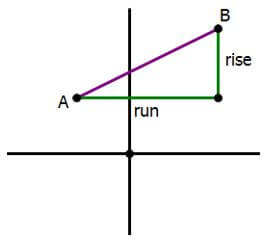
Even if you sketch this, you should be able to read the “rise” and “run” directly from the graph. Those are the legs of a right triangle, shown in green in this diagram. The distance between A & B is simply the hypotenuse of the slope triangle, so use the Pythagorean Theorem. That’s all you have to do to find distance in the coordinate plane.
GRE Geometry Equations & Formulas Are Good, But . . .
Finally, a word of caution. Knowledge of a formula, by itself, does not equal mathematical understanding. The GRE Quant doesn’t care about your memorization of formulas: instead, it designs problems specifically to probe your understanding. Yes, it’s important to be conversant in the formulas, but knowledge of these formulas is less than 10% of what you need to understand on the GRE Quant. For more on this, see this GMAT blog: even if you skip the three hard practice problems at the beginning, the rest of the discussion is quite pertinent to the GRE Quant as well as the GMAT.
GRE Geometry Formulas FAQ
What are the formulas in geometry?
Put very simply, geometry formulas are basic principles you can use to solve questions.
Of course (as we’ve seen in this post!), it’s not quite as simple as just plugging numbers blindly into a formula. The key to using geometry formulas is knowing when to use them: what kinds of questions they apply to and where to find the key numbers in the questions themselves.
The best way to master GRE geometry formulas? Practice, practice, practice!
How can I learn geometry easily?
The best way to truly master geometry painlessly isn’t rote memorization: it’s looking at principles in practice.
It can be tempting to sit down with a basic list of geometry formulas, memorize them, and brush off your hands. However, to really master geometry, it’s not just about learning the formulas—it’s about putting them into practice.
With that said, the easiest way to learn geometry is to see how formulas apply to a wide variety of question types. The key to this is to use high-quality materials to do a lot of geometry questions, then reading the answers and explanations after you’ve answered them—even if you’ve answered them correctly!
Why would you want to read question explanations if you’ve answered a question correctly? Because there may be a way to answer the question more quickly and efficiently than you did—and yes, this includes the use of geometry formulas!
P.S. If you’re looking for a shortcut for solving geometry equations, click here!
How important is geometry in the GRE as a whole?
Two-dimensional geometry appears in approximately 15% of GRE Quant questions, while coordinate geometry accounts for around 4.4% of the section and three-dimensional geometry rounds this off, comprising 2.2% of questions. Overall, geometry questions account for around 21.6% of your GRE Math score, or about 1 in 5 questions.
For more on where geometry sits in the “big picture” of GRE Quant, and what other Quant concepts you should study, check out our post What Kind of Math is on the GRE? Breakdown of Quant Concepts by Frequency.
Lastly, here is a full-length, free practice test from Magoosh that includes a detailed score report with a topic-by-topic breakdown of your performance. You can choose to do just the Quant section or a full length exam. Happy studying!